Nous allons nous intéresser à la durée du jour, plus exactement à la portion de journée où nous sommes éclairés par le soleil, par rapport à la nuit où nous nous trouvons dans l'ombre.

La terre tourne autour du soleil et décrit une orbite presque circulaire (en réalité une ellipse); en même temps elle tourne sur elle-même autour de son axe qui est incliné d'environ \(23°27'\) par rapport à la verticale sur le plan de son orbite (l'écliptique).

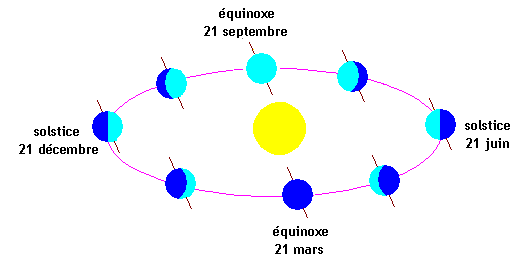
Une remarque préliminaire: il est évident qu'étant donnée la complexité du problème, nous le simplifierons: nous prendrons une orbite circulaire, nous ne nous occuperons pas des variations (précession, nutation) de l'axe de rotation de la terre, nous supposerons que le soleil est réduit à un point (pas d'aurore, ni de crépuscule, etc.)

Représentons la terre avec son axe de rotation vertical; en conséquence l'équateur sera situé dans un plan horizontal.

Supposons que ce jour-là, la terre soit dans une position telle que les rayons du soleil forment un angle \(\alpha \) avec le plan de l'équateur. Les spécialistes diront que l'angle \(\alpha \) mesure la "hauteur" de l'écliptique (plan de rotation du soleil) par rapport au plan de l'horizon. Remarquons que cet angle \(\alpha \) sera toujours compris entre \(-23°27'\) et \(+ 23°27'\). Pour que les choses soient plus gaies, nous avons choisi un des jours de l'année où α est positif. Dans l'hémisphère nord, nous sommes proches du solstice d'été !

Quelle sera la durée du jour à un endroit situé à une latitude \(\lambda \) ? Pour fixer les idées, plaçons-nous dans les environs de Bruxelles à 50° de latitude Nord.

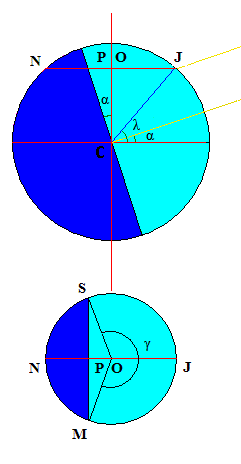Désignons par C le centre de la terre, et O le centre du parallèle de Bruxelles. Fixons un instant et désignons par M (matin) et S (soir) les deux points du parallèle de Bruxelles où le soleil se lève et se couche, tandis que J (jour) et N (nuit) seront ceux où il est respectivement midi et minuit. P sera le point où le plan du méridien de midi coupe la droite CO . Enfin, \(\gamma \) désignera l'angle MOS qui sous-tend la partie éclairée par le soleil. Pour simplifier le problème, supposons que pendant 24 heures la terre tourne sur elle-même sans modifier la position de son axe par rapport au soleil.

L'angle \(\gamma \) peut se calculer en remarquant que OP vaut, en valeur absolue, \(r\mathbf{cos~}(\pi-\gamma/2)\) où \(r\) représente le rayon du parallèle de Bruxelles. Connaissant la latitude \(\lambda \) de Bruxelles, on peut calculer \(r\) = OJ = R \(\mathbf{cos~}\lambda \) où R désigne le rayon terrestre. On a aussi CO = R .\(\mathbf{sin~}\lambda \) et dans le triangle COP , on a la relation OP = CO .\(\mathbf{tan~}\alpha \) = R .\(\mathbf{sin~}\lambda \mathbf{tan~}\alpha\). Enfin, en comparant les valeurs obtenues pour OP , on obtient : R \(\mathbf{cos~}\lambda.\mathbf{cos~}(\pi-\gamma/2)\) = R .\(\mathbf{sin~}\lambda.\mathbf{tan~}\alpha \) et \(\gamma\) est donné par la relation:

\[ \mathbf{cos~}(\pi-\gamma/2) = \mathbf{tan~}\lambda.\mathbf{tan~}\alpha ~~~~\text {ou encore}~~~~ \gamma=-2~\mathbf{arccos~}(\mathbf{tan~}\lambda.\mathbf{tan~}\alpha) \]

Aux équinoxes \(\alpha=0\) et \(\pi-\gamma/2=\pi/2\) c'est-à-dire \(\gamma=\pi \). La durée du jour est bien égale à celle de la nuit.

Au solstice d'été, \(\alpha=23°27'\). La latitude \(\lambda\) de Bruxelles est \(50°50'\) ; \(\mathbf{tan~}\lambda.\mathbf{tan~}\alpha\) \(=0,51695...=\mathbf{cos~}(\pi-\gamma/2)\) ce qui donne approximativement \(180°-\gamma/2=58°52'\) et \(\gamma=242°16'\), ce qui, traduit en nombre d'heures, vaut 16h 18 minutes.

En résumé pour calculer la durée du jour, il suffit de connaître deux choses: la latitude du lieu et l'angle \(\alpha\) selon lequel les rayons solaires tombent sur le plan de l'équateur à la date choisie. La valeur de cet angle est bien connue aux équinoxes (il vaut \(0°\)) et aux solstices (il vaut \(+23°27'\) et \(-23°27'\)). Mais aux autres dates ?

La réponse est fort simple. Au cours de sa rotation autour du soleil, l'axe de rotation de la terre reste parallèle à lui-même.

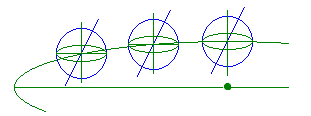
Imaginons-nous à présent, assis sur le soleil (rassurez-vous ce n'est qu'une fiction) et regardant tout au long de l'année en direction du centre de la terre. Cet axe nous paraîtra tourner autour d'une normale au plan de l'écliptique et décrira donc un cône dont le demi-angle au sommet vaut \(23°27'\).

Soit C le centre de la terre, A l'extrémité du vecteur unité CA dirigé suivant l'axe de rotation de la terre (dessiné en bleu) et CS un vecteur unité dirigé vers le soleil.

Rappelons que \(\alpha \) est l'angle formé par les rayons solaires, dirigés suivant le vecteur CS , et l'équateur; toutefois, il est techniquement plus commode de travailler avec la perpendiculaire CA au plan de l'équateur qui forme alors avec le vecteur C l'angle complémentaire de \(\alpha\). Comme les vecteurs CS et CA sont unitaires, le produit scalaire CS.CA = \(\mathbf{sin~}\alpha \).

Le but est donc d'établir la valeur d'un produit sclaire par le vecteur CS situé dans le plan de l'écliptique. Tout vecteur orthogonal à CS et, en particulier, ceux perpendiculaires à l'écliptique n'interviennent donc pas. Cette constatation nous permet de ramener le problème tridimensionnel à un problème plan par projection orthogonale sur le plan de l'écliptique.

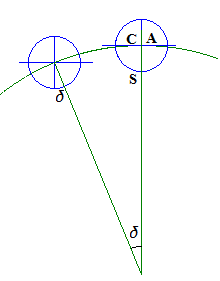
La terre munie de son axe (dessiné en bleu) décrit l'écliptique que nous avons convenu d'approcher par un cercle. Sur le schéma, nous avons supposé que la position initiale était à l'équinoxe (ici, celui de printemps); son axe est donc orthogonal à CS . Supposons qu'elle parcourt un arc de cercle d'amplitude \(\delta \); cet angle sera déterminé par la date comptée à partir de l'équinoxe de printemps. Si pour l'observateur situé au-dessus du plan de l'écliptique, elle ne change pas d'orientation, pour un observateur situé au soleil elle semblera avoir effectué une rotation d'amplitude \(\delta \) autour d'un axe perpendiculaire au plan de l'écliptique.

Afin de mieux voir ce qui se passe, zoomons sur ces deux positions et représentons les avec le vecteur CS orienté de la même manière. On obtient:

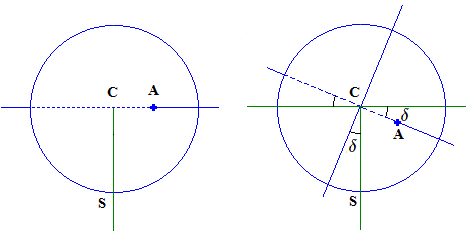
Le vecteur CA fait toujours le même angle \(23°27'\) par rapport à une perpendiculaire au plan de l'écliptique. La projection orthogonale de ce vecteur unité aura toujours le même module, à savoir \(\mathbf{sin~}(23°27')\). Pour obtenir le produit scalaire recherché, il nous reste à le multiplier par le cosinus de l'angle formé par CS et CA . Or cet angle est le complément de \(\delta \). Il en résulte que:

\( \mathbf{sin~} \alpha= \) CS.CA \(=\mathbf{sin~}(23°27').\mathbf{sin~}\delta\)   ou encore   \(\mathbf{sin~}\alpha=0.3979.\mathbf{sin~}\delta \)

À présent le problème est résolu et la durée du jour peut s'exprimer en fonction des deux variables: la date \(\delta \) (convertie de l'intervalle [0, 365) à [0, \(2\pi\))) et la latitude \(\lambda \) entre \([-\pi/2, \pi/2]\).

On aboutit à l'affreuse formule:

\[ \gamma = -2\mathbf{arccos~}(\mathbf{tan }\lambda.\mathbf{tan~}(\mathbf{arcsin~}(0.3979.\mathbf{sin~}\delta ))) \]

Heureusement, les outils informatiques sont à notre disposition pour calculer la valeur de \(\gamma \) qui sera transformée en vue d'être exprimée en heure depuis l'intervalle \([-2\pi, 0]\). Nous représenterons ci-dessous les variations de la durée du jour sur une année à des latitudes allant de \(0\) à \(90°\) réparties de \(10\) en \(10°\)

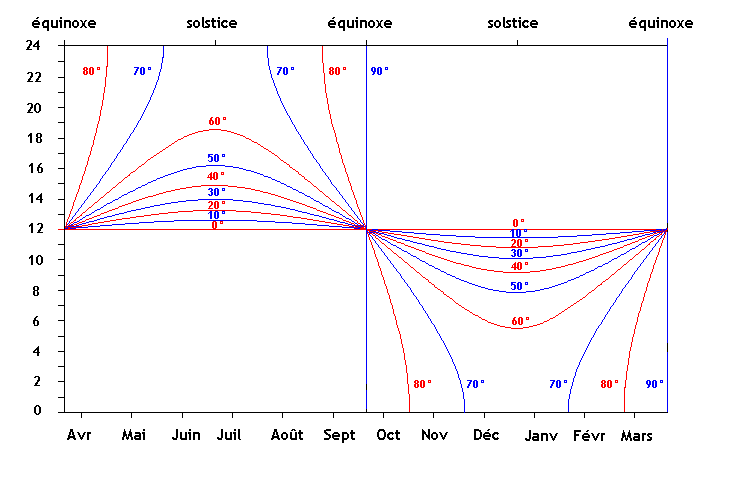
À partir de la latitude du cercle polaire, nous observons, en été, des périodes avec soleil ininterrompu (soleil de minuit) et, en hiver, des journées entières de nuit.

Ci-dessous vous trouverez une animation montrant les variations de la durée du jour en fonction de la latitude Nord (coin supérieur droit). La date comptée en jours à partir de l'équinoxe de printemps est reprise en abscisse et la durée figure en ordonnée. Remarque: pour la latitude Sud, les jours sont comptés à partir de l'équinoxe d'automne.

Cliquez sur l'image pour démarrer ou arrêter l'animation.

Pour Bruxelles (latitude = \(50°50'\)) on voit sur le graphique que la durée du jour varie approximativement entre les valeurs de 16h (solstice d'été) et 8h (solstice d'hiver). Si on souhaite plus de précision, le calcul de l'ensoleillement pour le solstice d'été (\(\delta=90°\) et \(\lambda=50,84°\)) donne un ensoleillement de 16h18m ce qui, compte tenu des nombreuses approximations, est fort proche des données des éphémérides (16h30m en 2013) soit moins de 2% d'écart.

Juste en dessous, vous pouvez apercevoir une autre visualisation de la durée du jour en fonction de la latitude. Le cercle extérieur représente 24h de durée du jour, celui au milieu 12h et le cercle central représente 0h ou 24h de nuit. Chaque trait correspond à la durée du jour en fonction de la latitude et du jour dans l'année (que vous pouvez modifier grâce au curseur situé juste en dessous). Il y a quelques problèmes de représentations liées à la stabilité numérique des équations pour les pôles lors de la transition entre la nuit polaire et le soleil de minuit lors des équinoxes.

Voir également l'article de Robert Ferréol