On distingue plusieurs types de billards, le billard "français", le plus courant dans la "vieille Europe", le snooker très prisé en Grande-Bretagne, et une variante simplifiée aux USA. A part cela il existe des billards "virtuels" inventés par les mathématiciens: le billard circulaire, le billard elliptique, etc.

Nous nous bornerons à considérer ici le billard français, appelé encore carambole.

Il s'agit d'une surface plane rectangulaire de 2,84m x 1,42m recouverte d'un tapis de feutre et cernée par quatre bandes de caoutchouc sur lesquelles la boule rebondit avec un maximum d'élasticité. Il y a trois billes (ou dit parfois boules), une rouge et deux autres destinées aux deux joueurs. Généralement celles-ci sont blanches et distinguées par la présence d'un petit point, mais parfois l'une est blanche et l'autre jaune pâle. Le but du jeu est de heurter sa bille de telle manière qu'elle s'en aille cogner les deux autres et réaliser un carambolage et de marquer ainsi un point. La réalisation du point permet au joueur de continuer; s'il échoue la main passe à son adversaire.

Le joueur heurte sa bille avec une queue. Le choc peut être dirigé à divers endroits et peut provoquer ce qu'on appelle un "effet"; la bille tournoie et ce mouvement de rotation modifie le rebond lors des chocs. L'étude de ce problème est assez compliquée; nous supposerons que le joueur heurte la bille par un choc dirigé vers le centre de celle-ci.

En décomposant le problème il faut donc, avec sa bille, heurter d'abord une des deux autres billes.

Rebond sur une bande

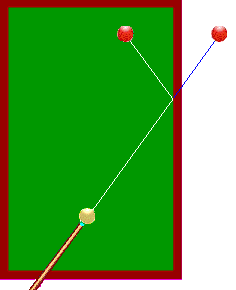
Comment se produit un rebond ? Tout simplement de la même manière que la réflexion de la lumière sur un miroir. La bille rebondit sur la bande en faisant un angle égal à l'angle sous lequel elle l'a touchée; en fait cette trajectoire minimise la distance parcourue. Si nous voulons toucher une bille en utilisant une seule bande, il nous faudra donc viser le symétrique de la bille par rapport à la bande choisie.

Le joueur est souvent aidé par la présence sur le bord du billard de différentes marques qui lui servent de points de repère pour mieux estimer la position de la symétrique de la bille visée.

Rebond sur deux bandes

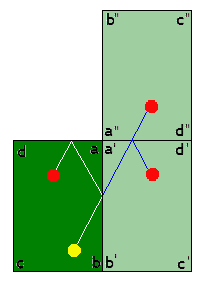
Il peut arriver que la disposition des billes impose au joueur de toucher une bille après deux rebonds. Cela peut se passer sur deux bandes parallèles ou deux bandes perpendiculaires.

Si les deux bandes sont perpendiculaires il s'agira de viser la symétrique de la symétrique de la bille. Or le produit de deux symétries d'axes perpendiculaires est rotation d'un demi-tour autour du point d'intersection (qui est tout simplement un angle du billard). La bille à viser est donc la symétrique par rapport au point a de la bille réelle.

Au cas où le joueur doit utiliser deux rebonds sur deux bandes parallèles, le produit des symétries est une translation dont l'amplitude vaut le double de la distance séparant les bandes.

Rebond sur trois bandes

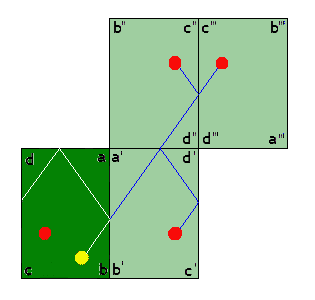
Nous regarderons ce qui se passe dans le cas le plus fréquent où les 3 bandes sont consécutives. Il faut donc faire le produit de trois symétries axiales. Nous venons de voir que le produit des deux premières est une rotation d'un demi-tour. Cette rotation, combinée avec une troisième symétrie axiale donnera une symétrie glissée.

Le joueur devra alors faire preuve d'un peu plus d'imagination pour visualiser la position de la bille à viser; il doit imaginer la position de la symétrique par rapport à \(ab\), ensuite la symétrique de celle-ci par rapport à \(a'd'\) (mais il peut s'aider du fait que c'est la symétrique de la bille par rapport au point a) et enfin la symétrique par rapport à \(c''d''\). En fait c'est le résultat d'un symétrie glissée d'axe \(da\) d'amplitude égale au double de la distance \(da\).

Tout cela paraît un peu compliqué, mais les joueurs sont tellement exercés qu'il a fallu créer un type de compétition dénommé "le trois bandes" qui leur impose de ne pouvoir réaliser le point qu'après avoir touché au minimum trois bandes ! Sans cela les joueurs très expérimentés réalisaient des centaines de points consécutifs.

Tout ceci ne concerne que le cas où la bille est heurtée centralement, et de plus uniquement la visée de la première bille ! Le problème général est bien plus compliqué et il est remarquable de voir comment les joueurs s'en tirent uniquement par leur expérience.

Les mathématiques ne constituent, au billard, qu'un tout premier pas...