Il est curieux que les théorèmes de Dandelin et Quételet , tous deux mathématiciens belges, soient enseignés à l'étranger sous le nom de théorèmes belges et ignorés dans notre pays. Peut-être le secret de cette méconnaissance réside-t-il tout simplement dans le fait que, pour être enseignés efficacement, ils nécessitent soit la construction d'un petit modèle soit la réalisation d'un dessin assez soigné.

Ces théorèmes relient en fait les définitions de coniques, section d'un cône, avec celle d'ellipse(hyperbole) ensemble des points dont la somme (différence) des distances à deux points fixes est constante ainsi que celle des trois coniques définies comme ensemble des points dont le rapport des distances à un point (foyer) et une droite (directrice) est une constante e appelée excentricité .

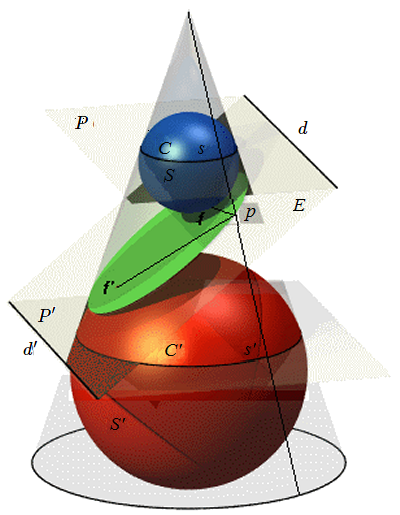Partons d'un cône (de révolution), et soit \(E\) un plan de section ; pour la commodité dessinons le cas où cette section est une ellipse. On peut dans ce cône trouver deux sphères \(S\), \(S'\) tangentes au cône le long d'un cercle \(C, C'\) et tangentes à \(E\) de part et d'autre de celui-ci ; \(f\) et \(f'\) désigneront les points de contact des sphères avec le plan. Nous noterons enfin \(P\) et \(P'\) les plans des cercles \(C\) et \(C'\) et \(d\) et \(d'\) les droites d'intersection de ces plans avec le plan \(E\). (Jusqu'ici le dessin peut se faire dans un plan perpendiculaire à \(p\) et la détermination des 2 sphères \(S\) et \(S'\) se ramène à la détermination de 2 cercles inscrits dans un angle au sommet d'un triangle).

Choisissons un point quelconque \(p\) de la section conique. Par ce point \(p\) menons la génératrice du cône qui coupe \(C\) et \(C'\) en \(S\) et \(S'\). On a évidemment pf = ps ; ce sont deux segments tangents à une sphère \(S\) ; de même \(pf' = ps'\), d'où \(pf+ pf' = ps + ps' = ss'\) c'est-à-dire la partie de génératrice comprise entre les plans \(P\) et \(P'\). Et bien évidemment, cette longueur est une constante indépendante du choix du point \(p\).

On retrouve donc la définition usuelle de l'ellipse comme ensemble des points dont la somme des distances à deux points fixes \(( f, f')\) est constante. On procéderait de même si la section était hyperbolique, la somme des distances serait tout simplement remplacée par la différence de celles-ci.

Que se passe-t-il si la section est parabolique ? Dans ce cas, la sphère \(S\) reste bien définie, la deuxième sphère \(S4\) est rejetée à l'infini (de même que son point de contact \(f'\)). Il faut alors songer à une propriété ne faisant intervenir que l'un des deux foyers.

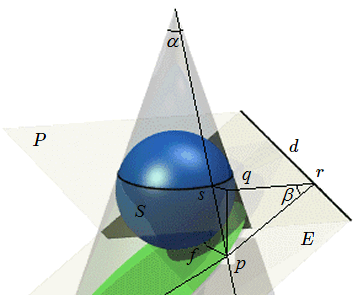Reprenons, en l'agrandissant légèrement, la figure de départ et portons notre attention sur la région située au voisinage du foyer \(f\).

Soit \(p\) un point quelconque de la conique. Sa projection orthogonale sur le plan \(P\) sera notée \(q\) et \(r\) désignera sa projection orthogonale sur la droite \(d\) ; le point \(s\) est sur la génératrice du cône passant par \(p\). En observant que l'angle \(spq\) vaut la moitié de l'angle \(\alpha\) au sommet du cône on a :

\[pf = ps ;~~pq = ps.\mathbf{cos~}(\alpha/2)~~;~~pq = pr.\mathbf{sin~}\beta\]

où \(\beta\) désigne l'angle des plans \(P\) et \(E\).

On en déduit :

\[ pf = pr.\frac{\mathbf{sin~}\beta}{\mathbf{cos~}(\alpha/2)}\]

ce qui montre que quel que soit \(p\) sur la section, le rapport de ses distances à \(f\) à la droite \(d\) est constante. Cette constante est l'excentricité \(\varepsilon\) de la conique.

Remarquons que dans le cas de la parabole, \(\beta\) et \(\alpha/2\) sont complémentaires et que la constante vaut \(1\) ; on retrouve la définition classique de la parabole ensemble des points équidistants d'une droite et d'un point.