A titre d'exemple traitons un petit exercice typiquement métrique: quel est l'ensemble des points d'où l'on voit une ellipse sous un angle droit ? Soit \(\mathbf{C}\) l'ellipse en question d'équation :

\[ ax^2 + by^2 = 1\] ou \[\mathbf{C}(x,x) \equiv ax^2+by^2-1=0 \]

et un point \(P\) de coordonnées \((x_0,y_0)\)

Rappel des notations:

Si \(P\) désigne un point donné de coordonnées \((x_0,y_0)\) et \(X\) un point quelconque de coordonnées \((x,y)\), on désigne par \(\mathbf{C}(X,X)\) une forme quadratique en \(x,y\) et \(\mathbf{C}(P,P)\) la valeur de cette forme au point \((x_0,y_0)\) ; enfin \(\mathbf{C}(X,P)\) est la valeur de la forme bilinéaire symétrique associée à la forme quadratique \(\mathbf{C}\) pour les points \((x_0,y_0)\) et \((x,y)\).

On obtient la forme bilinéaire symétrique en remplaçant dans la forme quadratique:

• les carrés du type \(x^2\) par les produits \(x_0x\)
• les termes produits de type \(xy\) par les sommes \(\frac{1}{2}(x_0y+xy_0)\),
• les termes linéaires du type \(x\) par les sommes \(\frac{1}{2}(x_0+x)\).

Nous avons vu que les tangentes issues de ce point ont pour équations:

\[\mathbf{C}^2(P,X) - \mathbf{C}(P,P).\mathbf{C}(X,X) = 0\] c'est-à-dire dans notre cas: \[(axx_0+byy_0-1)^2-(ax_0^2+by_0^2-1)(ax^2+by^2-1)=0\]

Les termes du second degré de cette équation sont:

\[ax^2(by_0^2-1)-2abx_0y_0xy+by^2(ax_0^2-1)\]

Les droites correspondantes seront perpendiculaires si la somme des coefficients des termes carrés en \(x\) et \(y\) est nulle; on obtient donc:

\[aby_0^2-a+bax_0^2-b=0\]

cela signifie que le point \(P\) de coordonnées \((x_0,y_0)\) est soumis à la condition:

\[x_0^2+y_0^2=\frac{a+b}{ab}\]

et l'on constate qu'il s'agit d'un cercle ; il est appelé cercle orthoptique, ou cercle de Monge .

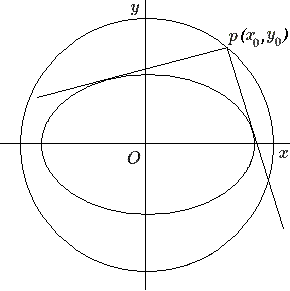
Cet exemple montre combien une étude préliminaire générale des coniques permet de regagner dans la suite le temps qui aurait été nécessaire à une étude détaillée et séparée de chacun des types de coniques.