Introduction
Une conique est en fait, une section conique, c'est-à-dire une ellipse , une hyperbole , une parabole , éventuellement deux droites, peut-être confondues.
Le lien entre les définitions "classiques" d'ellipse, parabole, hyperbole et la définition étymologique "section d'un cône" est assuré par les théorèmes belges .
Si l'on utilise des coordonnées, on constate que tous les exemples mentionnés plus haut sont des ensembles de points satisfaisant une équation du second degré en \(x, y\). Par exemple :
\[ y=ax^2+bx+c \] \[ y=\frac{ax+b}{cx+d} \] \[ x^2+y^2=r^2 \]Remarquons que la réciproque n'est évidemment pas vraie. Il est pourtant commode de définir une conique par une équation du second degré.
D'autre part comme il s'agit de sections coniques il est évident que les propriétés les plus fondamentales, les plus profondes seront les propriétés invariantes par projection centrale , autrement dit les propriétés projectives . Il est dès lors naturel d'utiliser les coordonnées adaptées à de telles propriétés, c'est-à-dire les coordonnées homogènes .
Propriétés projectives
Une conique \(\mathbf{C}\) peut donc raisonnablement être définie comme une équation (homogène) du second degré en les trois coordonnées homogènes \(X, Y, Z\).
Une conique \(\mathbf{C}\) détermine une relation entre les points du plan ; cette relation, projective, est liée à celle de conjugué harmonique ; on dira que deux points \(p_1\) et \(p_2\) sont conjugués (harmoniques) par rapport à la conique \(\mathbf{C}\) s'ils sont conjugués par rapport aux points d'intersection de la droite \(p_1p_2\) avec \(\mathbf{C}\) ; si cette droite ne coupe pas \(\mathbf{C}\) en des points à coordonnées réelles on s'en tirera soit en passant aux nombres complexes, soit plus simplement encore en remarquant que la condition de conjugaison par rapport aux racines d'une équation du second degré s'exprime en fonction des coefficients sans que l'on ait à calculer les racines. (Signalons l'intérêt de la représentation de deux couples de nombres conjugués harmoniques dans le plan de Gauss).
Points conjugués
Calculons (et ce sera pratiquement le seul calcul de toute la section consacrée aux coniques !) la condition pour que deux points \(p_1\) et \(p_2\) soient conjugués par rapport à la conique \(\mathbf{C}\) d'équation :
\[aX^2 + bY^2 + cZ^2 + 2dXY + 2eZX + 2f XY = 0\]Soient \((X_1, Y_1, Z_1)\) et \((X_2, Y_2, Z_2)\) les coordonnées des deux points \(p_1\) et \(p_2\) ; la droite qu'ils déterminent a pour équations paramétriques :
\[\begin{cases} X=\lambda X_1+\mu X_2\\ Y=\lambda Y_1+\mu Y_2\\ Z=\lambda Z_1+\mu Z_2\end{cases}\]Les deux points \(p_1\) et \(p_2\) correspondent aux valeurs \((1,0)\) et \((0,1)\) des paramètres \(\lambda\) et \(\mu\), c'est-à-dire que leur rapport \(k\) vaut soit l'infini soit zéro ; les points d'intersection de \(\mathbf{C}\) avec la droite \(p_1p_2\) sont donnés par les couples tels que :
\[a(\lambda X_1 + \mu X_2)^2 + b(\lambda Y_1 + \mu Y_2)^2 + c(\lambda Z_1 + \mu Z_2)^2 +\] \[2d(\lambda Y_1 + \mu Y_2)(\lambda Z_1 + \mu Z_2) + 2e(\lambda Z_1 + \mu Z_2)(\lambda X_1 + \mu X_2)+\] \[ 2f(\lambda X_1 + \mu X_2)(\lambda Y_1 + \mu Y_2) = 0\]En ordonnant l'équation par rapport aux paramètres on a :
\[\lambda^2(aX_1^2+bY_1^2+cZ_1^2+2dY_1Z_1+2eZ_1X_1+2fX_1Y_1)+\] \[2\lambda \mu(aX_1X_2 + bY_1Y_2 + cZ_1Z_2 + \] \[d(Y_1Z_2 + Z_1X_2) + e(Z_1X_2 + Z_2X_1) + f(X_1Y_2 + X_2Y_1))+\] \[\mu^2(aX_2^2+bY_2^2+cZ_2^2+2dY_2Z_2+2eZ_2X_2 +2fX_2Y_2)=0\]Cette relation fondamentale peut s'écrire de manière condensée sous la forme :
\[\lambda^2\mathbf{C}(p_1,p_1) + 2\lambda\mu\mathbf{C}(p_1,p_2) + \mu^2\mathbf{C}(p_2,p_2)=0\] où l'on a posé : \[\mathbf{C}(p_i,p_j)=aX_iX_j + bY_iY_j + cZ_iZ_j +\] \[ d(Y_iZ_j + Z_iX_j) + e(Z_iX_j + Z_jX_i) + f(X_iY_j + X_jY_i)\]Comme \(p_1\) et \(p_2\) correspondent aux valeurs infinie et nulle du rapport k des paramètres, les deux points d'intersection avec \(p_1\) et \(p_2\) seront conjugués (harmoniques) s'ils correspondent à des valeurs opposées de \(k\) ; autrement dit la somme des racines de l'équation aux points d'intersection doit être nulle, donc \(\mathbf{C}(p_1,p_2) =0\). \(\mathbf{C}(p_1, p_2)\) est la forme bilinéaire symétrique associée à la forme quadratique \(\mathbf{C}(p_1,p_2)\).
Notions dérivées
A partir d'ici tout devient simple:
- points conjugués :\(\mathbf{C}(p_i,p_j) = 0\)
- pôle et polaire (ensemble des conjugués du pôle \(p_1\)) : \(\mathbf{C}(p_i,x) = 0\)
- tangente au point \(p_1\) (avec \(\mathbf{C}(p_1,p_1)=0\)) : \(\mathbf{C}(p_i,x)=0\)
- point double : il se pourrait que \(\mathbf{C}(p_i,x)=0\) ne soit pas l'équation d'une droite, que \(\mathbf{C}(p_i,x)\) soit identiquement nul.
Que se passe-t-il dans ce cas ? Remarquons que :
\[\begin{cases} aX_1+fY_1+eZ_1=0\\fX_1+bY_1+dZ_1=0\\eX_1+dY_1+cZ_1=0\end{cases}\]Ce système homogène admet une solution non triviale, son déterminant est nul (et réciproquement s'il en est ainsi un tel point \(p_1\) existe). En utilisant les changements de coordonnées il suffit de voir ce qui se passe si \(p_1\) a pour coordonnées \((0, 0, 1 )\) ; dans ce cas \(e = d = c = 0\) et la conique a pour équation :
\[aX^2+bY^2+2fXY=0\]Elle est donc décomposée en deux droites se coupant précisément au point p' . Toute droite passant par p' couperait la conique en deux points confondus. Ce point est alors appelé point double.
- tangentes issues d'un point : on cherche les points \(x\) tels que \(px\) soit une tangente, c'est-à-dire que les points d'intersection de la droite \(px\) avec la conique \(\mathbf{C}\) soient confondus, autrement dit le discriminant de l'équation en les paramètres doit être nul : \[\mathbf{C}(p,x)^2- \mathbf{C}(p,p).\mathbf{C}(x,x)=0\]
- triangle autopolaire : étant donné une conique \(\mathbf{C}\) on choisit un point \(p\) qui ne lui appartient pas.
La polaire de ce point coupe la conique en deux points (sauf si la conique se réduit à une droite comptée deux fois) ; on choisit alors sur cette polaire un point \(q\) n'appartenant pas à \(\mathbf{C}\), et le point \(r\) sera le point d'intersection de la polaire de \(p\) avec celle de \(q\). Il en résulte que chacun des côtés est la polaire du sommet opposé. Si on choisit les trois points \(p\), \(q\), \(r\) comme points de coordonnées \((1,0,0), (0,1,0),(0,0,1)\), l'équation de \(\mathbf{C}\) se ramène à :
\[aX^2+bY^2+cZ^2=0\]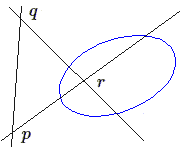
- Il existe une deuxième espèce de triangle autopolaire : on part également d'un point \(p\), mais on prend pour points \(q\) et \(r\) les deux points d'intersection de la polaire de \(p\) avec \(\mathbf{C}\) ; ces deux points sont distincts si la conique est proprement dite, non dégénérée. Dans ce cas, en adoptant les mêmes coordonnées, l'équation de \(\mathbf{C}\) se réduit à : \[X^2=aYZ\]
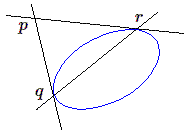
En choisissant convenablement l'unité on peut réduire l'équation à la forme :
\[X^2=YZ\]Sous cette forme, on obtient une paramétrisation de la conique \(\mathbf{C}\) par les équations :
\[\begin{cases} X=t\\ Y=1\\ Z=t^2\end{cases}\]La paramétrisation est obtenue par des fonctions rationnelles (même polynomiales), et l'on dit qu'une conique est une courbe rationnelle. Cette propriété est très importante et utilisée dans le calcul des primitives .
Les deux figures ci-dessus sont particulièrement intéressantes dans la mesure où elles permettent de dégager immédiatement les propriétés affines et euclidiennes des coniques .