A franchement parler, il est en général impossible de calculer la primitive d'une fonction donnée. Calculer signifiant obtenir le résultat exprimé au moyen de fonctions "élémentaires". Tout dépend, bien entendu, de ce que l'on appelle fonctions élémentaires. Il y aura évidemment toutes les fonctions rationnelles, les fonctions algébriques et quelques fonctions transcendantes telles les fonctions trigonométriques, exponentielles, leurs réciproques et ce que l'on obtient par composition de celles-ci. D'autres y ajouteront peut-être les fonctions gamma, les fonctions de Bessel, etc, mais dans l'enseignement secondaire on est limité à ce qui a été énuméré ci-dessus.

Il est déjà bien clair que si l'on ne connaissait pas certaines fonctions transcendantes on ne pourrait pas calculer la primitive de \(1/x\) ni celle de \(1/(1 + x^2)\) !

Toutefois, pour les fonctions rationnelles il existe une méthode mécanique qui permet de calculer les primitives à l'aide de fonctions rationnelles, logarithmiques et des fonctions goniométriques inverses. Cela mis à part on en est réduit à utiliser des astuces qui, parfois, réussissent en particulier avec les exercices proposés dans les manuels. On apprend ainsi une série de recettes: poser \(\sqrt{x^2+a^2}= x + t\) ou encore \(\sqrt{a^2 - x^2} = a \mathbf{cos~}t\), ... la seule justification habituellement donnée est que "cela marche" ! Ce n'est certainement pas par hasard et nous allons tâcher de mieux éclaircir les choses afin de ne plus devoir mémoriser ces recettes.

Soit à calculer une primitive de \(F(x, f(x))\) où \(F(x, y)\) est une fonction rationnelle des variables \(x \text{ et } y = f (x)\). Par contre \(f(x)\) est une fonction quelconque de \(x\). La méthode consiste à se ramener à une fonction rationnelle, fonction pour laquelle il existe une méthode standard. Il faudrait pour cela introduire une nouvelle variable, \(t\) par exemple, et exprimer rationnellement en fonction de \(t\) à la fois \(x\) et \(f(x)\).

Considérons la courbe \(y=f(x)\). Si cette courbe est rationnelle, par définition, les coordonnées d'un quelconque de ses points \((x, f(x))\) s'exprimeront rationnellement en fonction d'un paramètre \(t\). Nous pourrons alors prendre \(t\) comme nouvelle variable, effectuer la substitution dans l'intégrale et nous ramener à l'intégrale d'une fonction rationnelle.

Prenons quelques exemples classiques.

Soit tout d'abord à calculer la primitive de \(F(x,\sqrt{x^2 \pm a^2}\). Nous devons considérer la courbe d'équation: \(y = \sqrt{x^2 \pm a^2}\), c'est à dire la partie positive de la courbe \(y^2 = x^2 \pm a^2\). Cette courbe est une hyperbole dans le plan xy centrée à l'origine, dont les asymptotes sont les droites \(y = \pm x\).

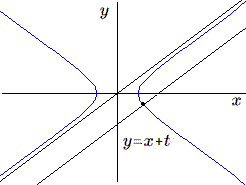
Nous savons que les hyperboles, et plus généralement les coniques sont des courbes rationnelles . Rappelons que l'on obtient une paramétrisation rationnelle en considérant un faisceau de droites passant par un des points de la conique; les coordonnées du second point d'intersection sont données par une équation du premier degré et sont donc des fonctions rationnelles du paramètre du faisceau. Dans le cas présent il suffit donc de choisir un point particulier de l'hyperbole, par exemple le point à l'infini sur l'asymptote \(y = x\), et de considérer le faisceau de droites par ce point; dans ce cas il s'agit des droites \(y = x + t, t\) étant le paramètre. On est dès lors assuré que les coordonnées \((x, y)\) des points de l'hyperbole sont fonctions rationnelles du paramètre \(t\), c'est-à-dire que \(x\) et \(\sqrt{x^2 \pm a^2}\) s'exprimeront en fonctions rationnelles de \(t\). L'intégrale peut alors se calculer par le procédé standard.

Considérons un deuxième exemple tout aussi classique.

Soit à calculer \(F(x, \sqrt{a^2 - x^2})\). Cette fois il faut considérer la courbe d'équation \(y = \sqrt{a^2 - x^2}\), ou encore \(x^2 + y^2 = a^2\), c'est-à-dire un cercle de rayon \(a\) centré à l'origine.

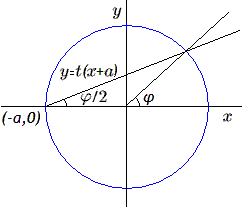
Comme précédemment nous allons exprimer les deux coordonnées \((x, y)\) d'un point de ce cercle en fonctions rationnelles d'un paramètre \(t\); pour cela choisissons un point du cercle, par exemple le point \((-a, 0)\). Le faisceau des droites passant par ce point \(a\) pour équation \(y = t(x + a)\); on peut aisément calculer les coordonnées d'un point du cercle et l'on obtient:

\[ x = a \frac {1 - t^2} {1 + t^2} \] \[ y = a \frac {2t} {1 + t^2} \]

On reconnaît la forme paramétrique \(x = a~\mathbf{cos~}\varphi, y = a~\mathbf{sin~}\varphi\) où sinus et cosinus ont été exprimés en fonctions rationnelles de \(\mathbf{tan~}\varphi/2\) (que l'on a posé ici \(t\)).

Dans d'autres cas analogues on procéderait de la même manière; toutefois il faut savoir qu'en général une courbe ne peut pas être paramétrisée rationnellement, et que par conséquent l'intégrale ne sera pas calculable au moyen des fonctions élémentaires.

On voit aussi la possibilité qu'offrent les intégrales de définir de nouvelles fonctions. Pour qui ne connaîtrait pas les fonctions logarithmiques et exponentielles, on pourrait définir la fonction logarithme népérien par la primitive de \(1/x\) s'annulant pour \(x = 1\) et \(\mathbf{exp} x\) comme fonction réciproque de la fonction logarithme; c'est d'ailleurs ainsi que Henri Lebesgue procédait, une méthode reprise par certains depuis lors.