Il est inutile de rappeler ici le théorème de Pythagore ; signalons toutefois quelques démonstrations particulièrement élégantes.

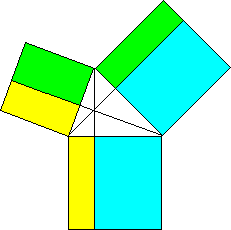
a) démonstration dite "chinoise" représentée ci-dessous:

b) démonstration due à Lebesgue , basée sur la remarque que seul importe le fait que les carrés soient des figures semblables; il suffit de remplacer les carrés par des triangles semblables au triangle initial.

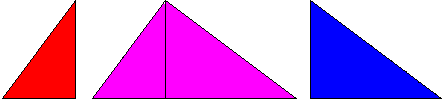
c) Cas particulier, dans le cas d'un triangle rectangle, du théorème affirmant que les rectangles de même couleur sont équivalents (commutativité du produit scalaire ).

d) Signalons également une démonstration animée .

Si on a fait choix d'une unité de longueur, le théorème devient numérique et on a \(a^2=b^2+c^2\) où \(a,b,c\) sont les 3 nombres réels mesurant les côtés du triangle. Chacun connaît la solution \((a,b,c)=(5,4,3)\); mais y a-t-il d'autres solutions entières? Bien entendu \((10,8,6),(15,12,9)...\) mais on peut alors se restreindre aux solutions naturelles où \(a,b,c\) n'ont pas de facteur commun.

Si \(a^2=b^2+c^2\), \(a,b\) et \(c\) ne sont pas simultanément pairs. Que \(a\) soit pair ou impair, \(a^2\) le sera également et un des deux carrés \(b^2\) ou \(c^2\) sera impair; supposons donc que ce soit \(b^2\) (et donc \(b\)) qui est impair. On peut écrire \(b^2=a^2-c^2=(a+c)(a-c)\). Décomposons le nombre impair \(b\) en facteurs premiers (2 n'apparaîtra pas) et notons \(p\) l'un de ses facteurs premiers. \(p\) ne pourra jamais diviser à la fois \(a+c\) et \(a-c\), sinon il diviserait leur somme \(2a\) (et donc \(a\)) et leur différence \(2c\) (et donc \(c\)); cela serait contraire au fait que \(a,b,c\) n'ont pas de facteur commun. Les facteurs premiers de \(b^2\) (avec leurs exposants pairs) se répartiront soit dans \(a+c\), soit dans \(a-c\) et par conséquent, chacun de ces deux nombres sera un carré. En posant \(a+c=m^2\) et \(a-c=n^2\), on obtiendra:

\[ a=\frac{m^2+n^2}{2}~~~~~c=\frac{m^2-n^2}{2}~~~~~b=mn \]

Remarquons que \(m^2\) et \(n^2\) diffèrent de \(2c\) et ont par conséquent même parité; \(a\) et \(c\) sont donc bien des naturels.

Pour tout couple de naturels premiers entre eux de même parité (donc tous deux impairs) avec \(m > n\), on obtient une solution (3 nombres naturels vérifiant la relation de Pythagore). On détermine ainsi toutes les solutions naturelles. Les premières sont:

\[ \begin{matrix} m & n & a & b & c\\ 3 & 1 & 5 & 3 & 4\\ 5 & 1 & 13 & 5 & 12\\ 5 & 3 & 17 & 15 & 18\\ 7 & 1 & 25 & 7 & 24\\ 7 & 3 & 29 & 21 & 20\\ ... & ... & ... & ... & ... \end{matrix} \]

La plus petite solution entière est donc le triangle d'hypoténuse \(5\) dont les côtés de l'angle droit valent \(3\) et \(4\), dont le périmètre vaut \(12\).

De là est née la " corde à 13 noeuds " (comportant \(12\) intervalles) qui a été utilisée dans l'antiquité par les architectes.

Le théorème de Pythagore est lié à la formule \(\mathbf{sin~}^2 \varphi+\mathbf{cos~}^2 \varphi=1\); on a \((\frac{b}{a})^2+(\frac{c}{a})^2=1\). Par conséquent on a résolu le problème de la détermination des angles dont les sinus et cosinus sont tous deux rationnels. On a:

\[ \mathbf{sin~}\varphi= \frac{2mn}{m^2+n^2}~~~~\text{et}~~~~\mathbf{cos~}\varphi= \frac{m^2-n^2}{m^2+n^2} \]

En divisant numérateur et dénominateur par \(m^2\) et en posant \(n/m=t\) on obtient :

\[ \mathbf{sin~}\varphi= \frac{2t}{1+t^2}~~~~\text{et}~~~~\mathbf{cos~}\varphi= \frac{1-t^2}{1+t^2} \]

et on retrouve ainsi les formules donnant le sinus et le cosinus d'un angle en fonctions rationnelles de la tangente de l'angle moitié.

Il est évident que si la tangente de l'angle-demi est rationnelle alors les sinus et cosinus le sont également.

La réciproque nécessite un petit calcul : si \(\mathbf{cos~}\varphi\) est rationnel alors \(t^2\) est également rationnel; mais si \(t^2\) et \(\mathbf{sin~}\varphi\) sont rationnels alors \(t\) l'est également. La condition est donc nécessaire et suffisante. Les sinus et cosinus d'un angle sont rationnels si et seulement si la tangente de l'angle demi est rationnelle.

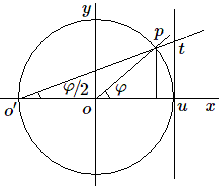Si l'on regarde les choses géométriquement il est évident que si \(\mathbf{sin~}\varphi\) et \(\mathbf{cos~}\varphi\) sont rationnels \(\mathbf{tan~}(\varphi/2)\) l'est également, puisque dans le cercle trigonométrique, \(\mathbf{tan~}(\varphi/2)=ut/2\) et que \(t\) est l'intersection d'une droite \(op\) de pente rationnelle avec la droite \(x=1\).

Géométriquement c'est la réciproque qui nécessite réflexion. Si \(\mathbf{tan~}(\varphi/2)\) est rationnel c'est-à-dire si les coordonnées de \(t\) le sont, \(p\) est un des points d'intersection de la droite \(o't\), à coefficients rationnels, avec le cercle. Mais les coordonnées des points d'intersection avec le cercle sont données par une équation du 2e degré à coefficients rationnels dont une des racines (celle correspondant à \(o'\)) est rationnelle; par conséquent l'autre l'est également. La condition est bien nécessaire et suffisante.

Cet exemple montre combien il est utile d'étudier un problème sous différents "angles".

Dans la question que nous avons traitée, la condition est évidemment suffisante lorsqu'on voit les choses algébriquement; elle est tout aussi évidemment nécessaire lorsqu'on adopte une vision géométrique. Par contre algébriquement on ne voit pas immédiatement que la condition est nécessaire et géométriquement il faut un peu réfléchir pour se rendre compte qu'elle est suffisante.