On a coutume de présenter le produit scalaire de deux vecteurs comme un nombre réel. Une définition possible est la suivante : le produit scalaire est le produit de la mesure d'un des vecteurs par la mesure de la projection orthogonale de l'autre. Toutefois, si on donne deux vecteurs et que l'on pose la question : "Quelle est la valeur du produit scalaire ? ", on se rend compte qu'il faut disposer d'une unité de mesure. Mais d'où viendrait cette unité de mesure ? Le bon dieu nous en aurait-il donné une ? Bien sûr que non ! Alors ne peut-on rien faire avec deux vecteurs ?

Il y a plus de deux mille ans, les Grecs utilisaient des notions géométriques liées aux segments. Ils parlaient du carré d'un segment (le carré ayant ce segment pour coté) et du rectangle de deux segments (le rectangle dont les côtés sont égaux aux deux segments).

Puisque le produit scalaire de deux vecteurs s'obtient en considérant l'un des vecteurs et la projection de l'autre, si nous ne disposons pas d'unité de mesure, nous dirons que c'est le produit des deux segments, c'est-à-dire le rectangle de deux segments ; il suffira d'y ajouter l'orientation.

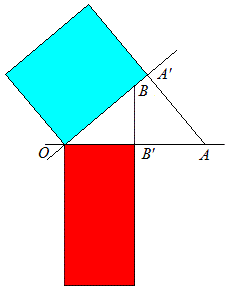
On peut alors facilement démontrer la commutativité du produit scalaire. La figure ci-dessus montre deux vecteurs \(OA\) et \(OB\). Si \(A'\) et \(B'\) désignent respectivement les projections de \(A\) sur \(OB\) et de \(B\) sur \(OA\), l'aire du rectangle de côtés \(OA\) et \(O'B\) et celle de celui de côtés \(OA'\) et \(OB\) sont égales. Lorsqu'un des côtés d'un rectangle glisse sur sa droite support, le rectangle devient un parallélogramme équivalent. On effectue cette transformation. Lorsque l'un des côtés du parallélogramme se confond avec un des vecteurs, on fait subir au parallélogramme une rotation d'un angle droit. On déforme ensuite ce parallélogramme jusqu'à ce qu'il redevienne un rectangle.

On a ainsi prouvé l'équivalence des deux rectangles et la commutativité du produit scalaire.

Si on dispose d'une unité de mesure et qu'on choisit le carré construit sur cette unité comme unité de mesure pour les surfaces, on retrouve la définition moderne du produit scalaire.

C'est cette vision géométrique du produit scalaire qui a permis aux Grecs d'énoncer et de démontrer le théorème de Pythagore .