La corde à treize nœuds est parfois appelée "corde des druides" ou "corde égyptienne". Il s'agit tout simplement d'une corde où l'on a effectué 13 nœuds consécutifs situés à des intervalles réguliers.

Son origine est mal connue ; elle a certainement été utilisée dans l'Egypte antique. Dans nos pays, on retrouve son emploi au Moyen âge chez les bâtisseurs.

Une utilisation très immédiate consiste en la construction d'angles droits. Tout maçon connaît la règle : "60 cm, 80 cm, 1 m" Pour vérifier la perpendicularité de deux murs, il suffit de mesurer à partir du sommet de leur angle : 60 cm sur l'un, 80 cm sur l'autre et de vérifier si les deux points obtenus sont bien distants de 1 m. La réciproque du théorème de Pythagore , nous dit que si \(a^2+b^2= c^2\), alors le triangle est droit et en effet \(60^2+80^2=100^2\). Remarquons que le pgcd de \(60, 80, 100\) vaut 20 et que ce triangle est semblable au triangle, 20 fois plus petit, de côtés \(3, 4\) et \(5\). La corde à 13 nœuds (qui présente 12 intervalles égaux) permet de construire immédiatement ce triangle \((3 + 4 + 5 = 12)\).

Ce célèbre triangle se retrouve sur des timbres-poste ; il doit sa célébrité au fait que c'est le "plus petit" triangle rectangle dont les mesures des côtés peuvent s'exprimer par des entiers.

Nous allons retrouver ce triangle d'une autre manière.

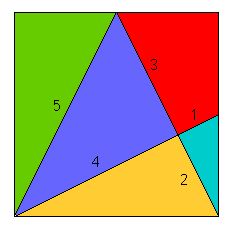Voici un carré de côté \(C\) partagé par 3 segments de droites, chacun passe par un sommet et aboutit au milieu d'un côté opposé. Beaucoup de triangles rectangles apparaissent sur cette figure. Par construction, nous avons en particulier plusieurs triangles rectangles dont les côtés de l'angle droit sont \(C\) et \(C/2\). Le petit triangle du coin inférieur droit est semblable à ces triangles. Si nous prenons le petit côté de l'angle droit comme unité de longueur, l'autre côté mesure donc \(2\) et l'hypoténuse (qui est égale à \(C/2\)) vaut \(\sqrt{5}\) ; \(C\) vaut donc \(2\sqrt{5}\).

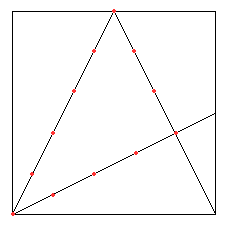
Partant de ce résultat on voit que chacun des 3 segments que nous avons tracés est l'hypoténuse d'un triangle rectangle de côtés \(C\) et \(C/2\) ; son carré vaut \(C^2+C^2/4=5C^2/4=25\) et l'hypoténuse mesure 5. On en déduit alors les mesures des autres segments de la figure qui valent 1, 2, 3, 4 et 5.

On retrouve, au centre de la figure, le fameux triangle de côtés 3, 4 et 5 qui peut être construit à l'aide de la corde à 13 nœuds.

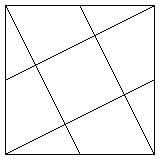Intéressons-nous à ces segments de mesure 5. Construisons l'un d'eux et ajoutons ceux obtenus à partir des rotations de quarts de tour. On obtient la figure ci-contre qui contient, au centre, un carré. Chacun des segments de longueur 5 est partagé en 2 segments de longueur 2 et un segment de longueur 1. Les 8 morceaux restants s'assemblent 2 par 2 pour former 4 autres carrés de côté 2. Le carré initial a été ainsi partagé en 5 figures égales.

On pourrait varier sur ce thème en partageant chaque côté en n parties égales.

On joint alors un sommet à un point du côté opposé et ensuite on trace toutes le parallèles passant par les points de subdivision. On fait tourner d'un quart de tour et on obtient ainsi une figure formée de carrés ainsi que de morceaux de carrés qui, comme dans le cas précédent, s'assemblent 2 par 2 pour former d'autres carrés égaux. A nouveau, on obtient une division en parties égales. Sur l'exemple ci-contre, on a subdivisé chaque côté en 5 parties et on a joint un sommet du carré au deuxième point de subdivision du côté opposé. Dans ce cas, on obtient après réunion des morceaux du puzzle, 29 pièces identiques. Pourquoi 29 ? Serait-ce parce que \(29 = 5^2 + 2^2\) ?

Il existe évidemment d'autres subdivisions d'un carré en parties égales, par exemple en construisant un simple damier, ou bien encore en joignant les milieux des 4 côtés. Mais serait-il possible de le partager en un nombre quelconque de parties égales ; en 3 par exemple ?

Voici une toute autre utilisation de la corde à 13 nœuds.

Nous avons rencontré un carré de côté \(C=2\sqrt{5}\). N'oublions pas que dans les constructions anciennes, on utilisait bien souvent le nombre d'or . Celui-ci vaut : \(\tau=(\sqrt{5} + 1)/2\) Il est donc aisé de l'obtenir en utilisant la corde à 13 nœuds.

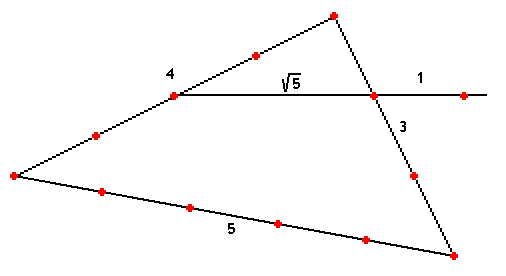
Le triangle de côtés 3, 4, 5 fournit l'angle droit ; on utilise alors le triangle rectangle de côtés 1, 2 dont l'hypoténuse vaut \(\sqrt{5}\) et on la prolonge d'une unité. Le segment ainsi construit vaut \(2\tau\).

La simplicité de cette construction explique probablement l'engouement suscité par le nombre d'or.