Soit l'hyperbole d'équation \(xy = 1\) ou encore la fonction \(y = 1/x\). Considérons l'aire comprise sous l'hyperbole limitée par la droite \(x = 1\) et par la droite \(x = t\) (et supposons \(t > 0\)

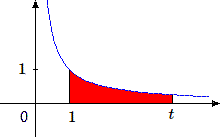
Pour qui connaît l'interprétation géométrique des intégrales, cette aire a pour valeur :

\[ \int_{1}^{t} {\frac {1}{x}} dx \]

Quant à calculer cette intégrale, ceux qui ne connaissent pas la fonction logarithme népérien ne peuvent résoudre le problème. (Qu'ils se consolent; en général, on ne sait pas calculer une intégrale , mises à part celles qu'on donne comme exercices !).

Cette aire est l'intégrale de 1 à \(t\) de la fonction \(1/x\) et est par conséquent fonction de la valeur de \(t\). On a donc ainsi défini une fonction \(L(t)\), et c'est d'ailleurs cette méthode que Lebesgue préconisait pour l'introduction de la fonction logarithme. Plus généralement de "nouvelles" fonctions peuvent être définies par des intégrales.

Quelles sont les propriétés de cette fonction \(L(t)\) ?

Elle est définie pour toutes les valeurs strictement positives de \(t\). Par définition même, on a:

• \(L(1) = 0\)
• \(t > 1 \implies L(t) > 0\)
• \(t < 1 \implies L(t) < 0\)

\(L(t)\) est une fonction strictement croissante.

Si \(t\) tend vers l'infini, alors \(L(t)\) tend également vers l'infini. Dans le cas où \(t\) croît, si on subdivise par les valeurs entières, l'aire est inférieure à la somme 1/2 + 1/3 + 1/4 + 1/5 + ... Or c'est la somme des termes d'une suite harmonique et cette somme tend vers \(+\infty\).

D'une manière analogue, en utilisant le rôle symétrique joué par \(x\) et \(y\) dans l'équation de l'hyperbole, on peut vérifier que lorsque \(x\) tend vers 0, la limite de L vaut \(-\infty\).

Nous allons montrer une propriété remarquable de cette fonction.

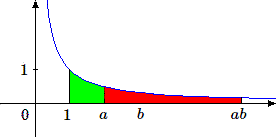
Calculons \(L(ab)\); c'est, par définition l'aire sous l'hyperbole comprise entre \(x=1\) et \(x=ab\). Cette aire peut être partagée par la droite \(x=a\).

On a \(L(ab) = L(a)\) augmenté de l'aire comprise entre les droites \(x=a\) et \(x=ab\). Pour en calculer la valeur, nous allons effectuer successivement deux transformations.

La première consiste à diviser les abscisses par \(a\); \(x\) devient \(ax\). L'hyperbole \(y=1/x\) devient l'hyperbole \(y=1/ax\), et toutes les aires sont divisées par \(a\).

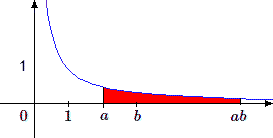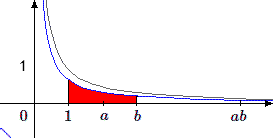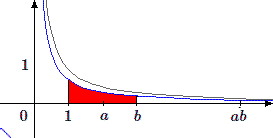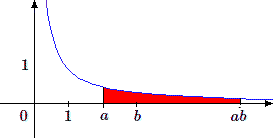La deuxième transformation consiste à multiplier les ordonnées par \(a\); \(y\) devient \(y/a\). Toutes les aires sont multipliées par \(a\) et l'hyperbole \(y=1/ax\) devient l'hyperbole \(y/a = 1/ax\) ou encore \(y = 1/x\), c'est-à-dire que l'on retrouve l'hyperbole de départ.

Au cours de la première transformation les points d'abscisses \(a\) et \(ab\) sont devenus les points d'abscisses 1 et \(b\), abscisses qui n'ont pas été modifiées par la seconde transformation. L'aire initiale limitée par les droites \(x=a\) et \(x=ab\) est équivalente à celle limitée par les droites \(x=1\) et \(x=b\). Elle a donc pour valeur \(L(b)\).

En fait, on a composé la première transformation \(x'=x/a, y'=y\) avec la deuxième \(x"=x', y"=ay'\). Le résultat est la transformation d'équations: \(x"= x/a, y"=ay\) qui conserve évidemment l'hyperbole. Il s'agit d'une application linéaire nommée "rotation hyperbolique" dont le déterminant vaut 1 et conserve donc les aires.

On obtient ainsi la propriété fondamentale de la fonction \(L\).

\[L(ab) = L(a) + L(b)\]

On en déduit immédiatement que pour tout naturel \(n\), \(L(a^n) = nL(a)\). En travaillant encore un peu, on montre que cette formule reste valable pour tout \(n\) rationnel.

Si on a étudié les logarithmes en base 10, ou même en base \(k\), on reconnaît toutes les propriétés de la fonction logarithme. Mais quelle est la base de ceux-ci ?

Il suffit de déterminer la valeur de \(t\) pour laquelle l'aire située sous la courbe vaut 1. On peut procéder par approximation, en estimant des bornes inférieures et supérieures pour cette aire et on arrive ainsi facilement à voir que cette valeur est comprise entre 2,5 et 3. En fait elle vaut environ 2,71828... et est notée \(e\). C'est la base des logarithmes népériens (dus à Napier ). La fonction \(L\) est généralement notée \(\mathbf{ln}\). On rencontre également \(\mathbf{Log}\) ou bien encore \(\mathbf{log_e}\) ; dans ce cas \(\mathbf{log}\) est réservé au logarithme en base 10.