Les coordonnées dites cartésiennes conviennent parfaitement lorsqu'il s'agit de repérer des points situés à distance finie. Toutefois dès qu'il s'agit de travailler avec des points à l'infini elles se révèlent inadaptées. Il existe des coordonnées mieux adaptées, en particulier les coordonnées trilinéaires .

L'utilisation des points à l'infini est indispensable pour l'étude de propriétés projectives , et en particulier si l'on veut faire de manière simple, économique et concise une théorie des coniques .

L'idée de base pour introduire les points à l'infini est celle de projection centrale (ou projection conique). La projection d'un plan \(\alpha\) sur un autre plan \(\beta\) à partir d'un centre de projection \(o\) est "à peu près" une bijection.

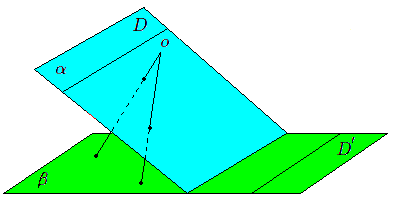
Seule une droite \(D\) de \(\alpha\) (l'intersection du plan parallèle à \(\beta\) par \(o\)) ne possède pas d'image, et seule une droite \(D'\) de \(\beta\) (l'intersection du plan parallèle à \(\alpha\) par \(p\)) n'est l'image d'aucun point de \(\alpha\). Cette projection devient une bijection si l'on ajoute à chacun des deux plans \(\alpha\) et \(\beta\) une droite de points à l'infini. Dès lors à chaque point du plan (y compris les points à l'infini) correspond une projetante par \(o\).

Pour introduire des coordonnées pour ces points il nous suffira donc d'en introduire pour les projetantes par \(o\). Mais alors notre plan se présente comme plongé dans un vectoriel V de dimension 3 de neutre \(o\).

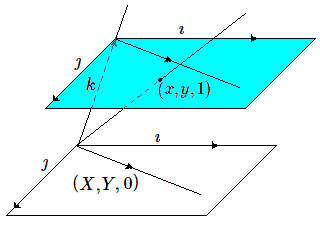
Le plan \(\alpha\) étant coordonné, d'origine \(o'\) et doté d'une base \((\imath, \jmath)\), munissons le vectoriel d'une base formée des vecteurs \(\imath\) et \(\jmath\) ainsi que du vecteur \(k = oo'\). Dès lors le plan \(\alpha\) a pour équation \(z = 1\), et tout point de coordonnées \((x, y)\) (à distance finie de \(\alpha\) possède 3 coordonnées \((x, y, 1)\) dans le vectoriel. Sa projetante est le sous-vectoriel \((kx, ky, k)\). Quant aux points à l'infini de \(\alpha\) , ils sont déterminés par leur direction. Soit un point à l'infini dans la direction du vecteur \((X, Y)\) de \(\alpha\); sa projetante est parallèle à \(\alpha\) et correspond au sous-vectoriel \((kX, kY, 0)\).

En résumé tous les sous-vectoriels sont des projetantes, et ceux ayant leur dernière coordonnée nulle correspondent aux points à l'infini.

Nous avons ainsi défini pour tous les points du plan, y compris les points à l'infini, des coordonnées: il s'agit de 3 nombres non simultanément nuls. Les coordonnées \((X, Y, Z)\) sont données à un facteur non nul \(k\). Si \(Z\) est nul, le point est le point à l'infini dans la direction du vecteur \((X, Y)\); si \(Z\) est non nul, le point est le point de coordonnées cartésiennes \((x = X/Z, y = Y/Z)\).

Etant donné la construction de ces coordonnées à partir d'un vectoriel, on trouve immédiatement les équations des droites. Les sous-vectoriels à deux dimensions sont les combinaisons linéaires de deux sous-vectoriels à une dimension. On a:

\[ \begin{cases}X = \lambda X ' + \mu X '' \\ Y = \lambda Y ' + \mu Y '' \\Z = \lambda Z ' + \mu Z '' \end{cases} \]

On peut également dire que le vecteur \((X, Y, Z)\) est combinaison linéaire des deux vecteurs \((X', Y', Z')\) et \((X'', Y'', Z'')\), ce qui s'exprime par le fait que le déterminant \(D\) est nul.

\[ D = \left|\begin{array}{cc}X& Y& Z\\X '& Y '& Z '\\X ''& Y ''& Z '' \end{array} \right| \]

On voit ainsi qu'une droite possède une équation homogène du premier degré en \(X, Y, Z\), ce qui justifie le nom de coordonnées homogènes.

Elle doit toujours être homogène en les trois coordonnées. Plus généralement, toute relation écrite en coordonnées homogènes doit toujours, pour avoir du sens, être homogène; cela évite bien des fautes d'attention !