Ce théorème, dû à Viviani , s'énonce:

La démonstration de cette propriété est fort simple:

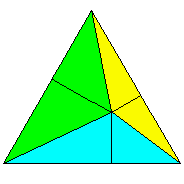
Dans le triangle \(abc\) on choisit un point intérieur \(p\) quelconque; soient \(h', h''\) et \(h'''\) les distances aux 3 côtés \(bc, ca\) et \(ab\). L'aire \(T\) du triangle \(abc\) vaut la somme des aires des 3 triangles \(pbc, pca\) et \(pab\), ce qui donne:

\[ T = \frac{h'.bc + h''.ca + h'''.ab}{2}\]

et, en désignant par \(C\) la longueur du côté du triangle équilatéral et par \(h\) la hauteur:

\[ T = \frac{(h' + h'' + h''')C}{2} = \frac{h.C}{2}\]

On remarque que ce théorème se généralise en dimension quelconque et est également valable pour un point \(p\) extérieur au triangle à condition de tenir compte des signes.

On voit ainsi qu'un point quelconque du plan peut être repéré par ses 3 "distances" aux côtés du triangle ou, puisque leur somme est fixée, par les rapports mutuels de ces distances c'est-à-dire par 3 nombres donnés à un facteur près.

Cette propriété remarquable donne naissance à un système de 3 coordonnées, dit "trilinéaires", données à un facteur près, c'est-à-dire des coordonnées homogènes .

On peut voir les choses un peu différemment. Soient trois réels positifs \(x, y, z\) de somme fixée valant \(k\). Comme il s'agit de trois nombres réels, on peut les regarder comme points d'un vectoriel à 3 dimensions; mais la relation \(x + y + z = k\) signifie que les points sont situés dans un plan. De plus comme ces trois quantités sont positives, les points sont à l'intérieur du premier octant. Il s'agit donc des points intérieurs au triangle.

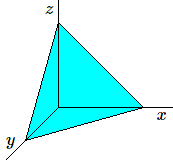
De plus on voit que toute relation linéaire entre \(x, y\) et \(z\) correspond dans l'espace à un plan et par conséquent, dans le plan du triangle à une droite.

Ces coordonnées sont fort utiles, en particulier, si l'on est face à un problème où les êtres étudiés sont caractérisés par les rapports de trois grandeurs. On peut les représenter par des points intérieurs à un triangle équilatéral.

Cette situation se présente dans de nombreux problèmes: citons par exemple, la valeur énergétique des éléments (protides, glucides et lipides), les matériaux de construction (sable, argile et calcaire), les élections (lorsque trois partis sont en présence), les couleurs en synthèse additive (rouge, vert, bleu) ou soustractive (jaune, cyan et magenta), les questionnaires à choix multiple (vrai, faux ou abstention).