Certains pays élisent leurs représentants dans un système dit "à la proportionnelle". Avez-vous déjà réfléchi à la manière dont fonctionne ce système ? Nous allons dans cette section prendre un exemple simplifié qui nous montrera que les choses ne sont pas aussi évidentes que l'on croit.

Supposons donc pour simplifier, tout en évitant une situation simpliste, que seuls trois partis sont en présence et qu'il y a 7 sièges à pourvoir. Des élections ont lieu et donnent pour résultat:

Parti A	400 voix	400/7 = 57,142...%
Parti B	100 voix	100/7 = 14,283...%
Parti C	200 voix	200/7 = 28,571...%

Dans cette surprenante éventualité, aucun problème: le parti A reçoit 4 sièges, le parti B, 1 siège et le parti C, 2 sièges. Evidemment dans la réalité les résultats ne seront pas aussi miraculeusement simples et on pourrait avoir:

Parti A	49%
Parti B	16%
Parti C	35%

Que devient la répartition des sièges ? Le nombre de représentants est un nombre entier (ce qui n'implique pas que ceux-ci soient intègres !). Comment dès lors répartir les 7 sièges vacants ?

De fait, les modes d'attribution varient suivant les pays (utilisant la proportionnelle), et même en Belgique, la répartition diffère suivant qu'il s'agit d'élections législatives ou communales. Pour représenter la situation nous allons utiliser les coordonnées trilinéaires .

Dans notre problème, le résultat d'un vote pourra ainsi être représenté par un point intérieur au triangle tel que \(h'/h, h''/h\) et \(h'''/h\) soient les 3 pourcentages recueillis par les partis \(A, B\) et \(C\). Certains résultats ne poseront aucun problème pour la répartition des sièges, lorsque la représentation proportionnelle donne des nombres entiers, mais en général le point représentatif ne coïncidera pas avec un de ces points privilégiés et il faudra alors se définir une règle qui assimilera ce point au point le plus "proche".

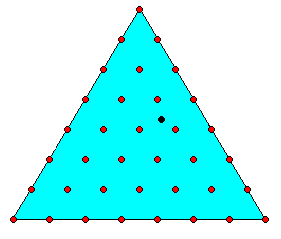
Le triangle sera alors découpé en régions (qu'il est raisonnable de supposer simplement connexes, bordées par des arcs différentiables, "centrées" en les points remarquables bien que ces hypothèses ne soient pas indispensables dans la suite).

Remarquons qu'à ce stade il y a déjà un paradoxe inévitable: un parti peut augmenter le nombre de ses voix et perdre un siège ! 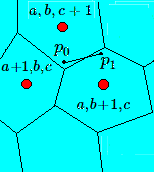En effet, si le résultat d'un parti reste constant, le point représentatif reste sur une parallèle à un des côtés du triangle. Soit un point frontière à 3 régions correspondant aux 3 répartitions \((a, b, c + 1)\), \((a, b + 1, c)\) et \((a + 1, b, c)\); en ce point, comme la somme des angles vaut 360° il existe au moins une parallèle à un des côtés qui traverse les 3 régions. En déplaçant légèrement cette droite et en l'inclinant on obtient la situation:

En se déplaçant de \(p_0\) à \(p_1\), le parti \(C\) augmente son score et passe de c + 1 sièges à c sièges !

Cette anomalie est inéluctable et aucun système proportionnel ne peut l'éviter. Il faut donc en prendre son parti (sans jeu de mots) et se définir une règle d'attribution des sièges la moins mauvaise possible. L'idée la plus naturelle est de choisir le point privilégié le plus proche du point p ; on obtient ainsi un découpage en hexagones réguliers.

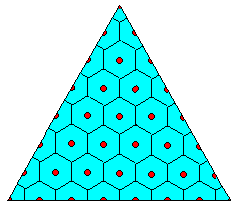
Cette règle (dite de Hamilton ou des plus grands restes) revient à attribuer aux partis les parties entières de leurs quotas et à répartir les sièges restants aux partis ayant les restes fractionnaires les plus élevés. Dans notre exemple:

partis	\(A\)	\(B\)	\(C\)
pourcentages	49%	16%	35%
quotas	3,43	1,12	2,45
sièges directs	3	1	2
sièges restants	0	0	+1
résultat	3	1	3

Cette méthode peut paraître excellente mais un examen plus critique peut l'ébranler. Tout d'abord on utilise dans le plan la métrique euclidienne alors qu'en fait les comparaisons de longueurs n'ont de sens que dans 3 directions. D'autre part peut-on parler d'égalité de longueur ? Peut-on dire qu'il y a la même différence entre un parti qui passe de 5% à 10% et un autre qui passe de 75% à 80% ? En outre un nouveau paradoxe apparaît.

Considérons 2 élections successives donnant les résultats suivants:

Election1	pourcentages	76%	5%	19%
	quotas	5,32	0,35	1,33
	sièges	5	1	1
Election2	pourcentages	67%	9%	24%
	quotas	4,69	0,63	1,68
	sièges	5	0	2

Si nous comparons les scores des partis \(B\) et \(C\), nous remarquons que dans la première élection le parti \(C\) obtient près du quadruple (exactement 3,8) des voix du parti \(B\); lors de la deuxième élection il fait moins du triple (exactement 2,66..) des voix du parti \(B\). Pourtant lors de la deuxième élection, si le résultat du parti A reste inchangé (5 sièges), le parti \(B\) perd son siège en faveur du parti \(C\), alors que c'est la parti \(C\) qui perd relativement à \(B\) !

Nous pouvons éviter ce paradoxe en demandant que les frontières entre les régions de découpage soient des segments de droites passant par les sommets du triangle. Toutefois cette condition est trop faible pour déterminer entièrement la règle de répartition et il existe dans la pratique plusieurs méthodes qui respectent cette contrainte.

En Belgique le système D'Hondt, analogue au système Jefferson, en est un exemple. Toutes ces méthodes, connues sous le nom de méthodes de diviseurs, fonctionnent de la manière suivante: on choisit un pourcentage correspondant à la "valeur" d'un élu de telle sorte qu'en divisant les quotas par ce pourcentage et en "arrondissant", on obtienne un total égal au nombre de sièges à pourvoir. Les variantes proviennent de la manière dont on arrondit; le type d'arrondissement peut être arithmétique (on arrondit à l'entier supérieur lorsque l'on dépasse la moyenne arithmétique), harmonique (lorsqu'on dépasse la moyenne harmonique), géométrique ou de tout autre type.

Le système D'Hondt utilisé en Belgique pour les législatives correspond à un arrondissement arithmétique. Il est formulé de manière légèrement différente mais équivalente:

On attribue à chaque parti un nombre d'élus égal à la partie entière du quota. On calcule ensuite la "valeur" qu'aurait un élu si on attribuait aux partis un siège, deux sièges,... supplémentaires; on attribue alors les sièges dans l'ordre décroissant des valeurs obtenues. Sur notre exemple on a:

partis	\(A\)	\(B\)	\(C\)
pourcentages	49%	16%	35%
quotas	3,43	1,12	2,45
valeur(1)	3.43	1,1	2,45
valeur(2)	1,715	0,56	1,225
valeur(3)	1,143...	0,373...	0,816...
valeur(4)	0,8575	0,28	0,6125
résultat	4	1	2

Puisqu'il y a 7 sièges à pourvoir, on prend les 7 plus grandes valeurs apparaissant dans le tableau ci-dessus, c'est-à-dire: 3,43 2,45 1,715 1,225 1,143... 1,12 0,875. (le diviseur d est 11,66...% < d < 12,25%) Ce système favorise les "grands" partis, comme cela se voit sur la figure ci-dessous:

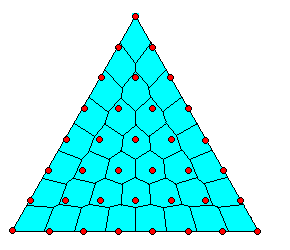
D'autres systèmes (le système Adams, par exemple) favorisent au contraire les "petits" partis. Le choix d'un bon système électoral est dès lors une question assez subjective, ce qui explique la diversité des systèmes existants.

Revenons au départ. Supposons des élections donnant comme résultats (en pourcentages):

Parti \(A\):	70,5%
Parti \(B\):	18,8%
Parti \(C\):	10,7%

La répartition des sièges donnera aux partis \(A\), \(B\) et \(C\) respectivement 7, 2 et 1 sièges. Supposons de nouvelles élections donnant comme résultats:

Parti \(A\):	68%
Parti \(B\):	16,8%
Parti \(C\):	15,2%

La répartition sera cette fois 8, 1 et 1 sièges. Il y a perte d'un siège par le parti \(B\) au profit du parti \(A\). Et pourtant le parti B n'a perdu que 2% du total des suffrages exprimés, c'est-à-dire moins que le parti \(A\) qui en a perdu 2,5%.

De nouveau cette situation peu paraître injuste et on serait tenté d'en revenir à la méthode de Hamilton ! Tout dépend en fait de voir si l'on accorde plus de poids aux pourcentages relatifs qu'aux pourcentages absolus.

La perfection n'est pas de ce monde !