Nous vivons dans un monde haut en couleurs. Mais combien en existe-t-il en réalité ? Quelle question !

On pense d'abord aux sept couleurs de l'arc-en-ciel, mais pourquoi sept? Peut-être parce que sept était un nombre "magique": il y a les sept merveilles du monde, les sept collines de Rome, le chandelier à sept branches, les sept jours de la semaine et aussi les sept péchés capitaux ! Pourtant la réalité est plus simple. On utilise trois couleurs dites fondamentales. Mais quelles sont-elles ?

Il faut distinguer la manière dont s'effectue la synthèse des couleurs. Elle peut être additive (on part du noir et l'on ajoute des couleurs) ou bien soustractive (on part du blanc et on obscurcit au moyen de couleurs).

Considérons tout d'abord le premier cas; c'est celui qui est utilisé en télévision ou sur le moniteur de votre ordinateur. Les trois couleurs fondamentales sont le rouge (\(R\)), le vert (\(G\) pour green) et le bleu (\(B\)). L'éclairement simultané par du rouge et du vert donne du jaune (\(Y\) pour yellow); du bleu et du vert donnent une couleur turquoise appelée cyan (\(C\)) et enfin le rouge et le bleu se combinent pour donner un violet appelé magenta (\(M\)).

Enfin un éclairement simultané par les trois couleurs de base donne du blanc. Bien entendu, on peut régler l'intensité de chacune des trois couleurs fondamentales et obtenir ainsi toutes les couleurs possibles. Par exemple un rouge intense combiné à un vert peu intense donnera de l'orange.

On peut ainsi représenter les différentes couleurs en donnant la contribution de chacune des trois couleurs fondamentales (p.ex. pour de l'orange 67% \(R\), 33% \(G\), 0% \(B\)). On peut ainsi représenter les couleurs à l'aide de coordonnées trilinéaires . Bien entendu l'intensité des couleurs n'est pas définie: 100% de rouge peut donner un rouge vif mais aussi un rouge plus clair voire un rose très pâle !

Passons maintenant à la synthèse soustractive des couleurs. C'est ce qui se passe lorsque l'on dessine avec des crayons de couleurs ou que l'on peint avec de l'aquarelle. Cette fois les couleurs "fondamentales" sont le jaune , le cyan et le magenta . En superposant du jaune et du magenta on obtiendra du rouge (le jaune "mange" le bleu du magenta); de même du jaune et du cyan donneront du vert et la superposition du magenta et du cyan donnera du bleu. Enfin la superposition des trois couleurs fondamentales donnera du noir. On peut comme précédemment définir chaque couleur à l'aide des pourcentages relatifs de chacun des composants.

En retournant à la définition par \(RGB\), les couleurs sont représentées par les points d'un cube, un des sommets correspond au noir \((0, 0, 0)\) et le sommet opposé au blanc \((1, 1, 1)\). Nous avons choisi l'unité correspondant aux 3 couleurs fondamentales dans leur intensité maximum.

Le lien entre \((R, G, B)\) et \((C, M, Y)\) est évident:

Il existe d'autres moyens de représenter les différentes couleurs.

Songeons à une couleur quelconque représentée par \((R, G, B)\). Si nous éclairons un écran par les 3 projecteurs \(RGB\) en augmentant progressivement leur intensité, nous obtiendrons, à partir de cette couleur, une teinte d'abord fort sombre, puis de plus en plus intense, jusqu'à ce que les projecteurs atteignent leur intensité maximum. La couleur sera alors à son maximum de brillance. Les trois nombres \(R, G, B\) auront été multipliés par une même constante, jusqu'à ce que le plus grand d'entre eux atteigne la valeur maximum 1. Nous aurons en fait parcouru un segment situé sur une droite issue de l'origine, partant du point \((R, G, B)\) et aboutissant dans l'une des trois faces opposées.

Etant donnée cette même couleur on peut progressivement la délaver; pour cela maintenons inchangé le projecteur de plus grande intensité (supposons \(R\gt G\gt B\) et laissons donc fixe le projecteur rouge) et augmentons l'intensité des deux autres de telle manière à obtenir la même intensité \(R = G = B\). Nous sommes restés dans un plan parallèle à l'un des 3 plans coordonnés (dans ce cas le plan \(R\)=0) et nous sommes partis du point \((R, G, B)\) pour aboutir sur la grande diagonale du cube au point \((R, R, R)\). Le support de ce segment perce un des plans coordonnés (\(B = 0\) en l'occurrence) en un point correspondant à la couleur la plus saturée.

Une nouvelle représentation des couleurs s'impose: donner sa teinte (hue) et ensuite son degré de luminosité (brillance) et de saturation. C'est la représentation \(HSB\) ou \(TLS\).

Comment définir la teinte ? Notre oeil perçoit les couleurs lorsque leur longueur d'onde est approximativement comprise entre 400 et 800 nanomètres. En terme de fréquences, cela va du simple au double; 400 et 800 nm correspondent à un rouge violacé. De même qu'en musique un son et celui de fréquence double nous donnent la même impression (nous leur attribuons d'ailleurs le même nom) les deux couleurs extrêmes du spectre visible ont des fréquences telles que nous leur donnons le même nom.

Le spectre visible part du rouge violacé, violet, indigo, bleu, vert, jaune, orange, rouge, pour revenir au rouge violacé; il se referme ainsi et peut être représenté sur un cercle. Chaque teinte est définie par un angle. On peut considérer le demi-plan passant par la grande diagonale du cube et le point correspondant à la couleur et le caractériser par son angle avec un demi-plan de référence, \(R=0\), par exemple. Choisissons une couleur \(C\) nuance d'orange, correspondant à \((R, G, B)=(0.60, 0.36, 0.12)\); elle est la somme de \((0.48, 0.24, 0)\) et du gris \((0.12, 0.12, 0.12)\). Voici toutes les nuances de la teinte orange (2/3 de rouge 1/3 de vert): \(T\) (ou H: Hue)=30°.

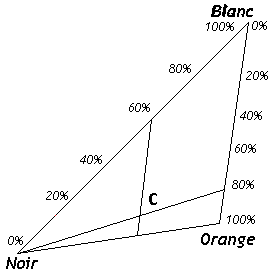Il reste à préciser la luminosité (brillance) et la saturation. La luminosité \(L\) (ou \(B\): Brightness) = max \((R, G, B)\); elle est constante sur les parallèles au côté blanc-orange et vaut, pour la teinte \(C\) choisie 0.60. La saturation \(S\) (Saturation) = 1 - (min\((R, G, B)\))/\(L\); elle est constante sur les droites issues du sommet correspondant au noir; dans notre exemple elle vaut 0.80. On obtient ainsi une autre représentation de l'ensemble des couleurs.

Tout cela paraît maintenant très clair (sans jeu de mots) mais il faut remarquer que jamais nous n'avons précisé les couleurs fondamentales ; le rouge, par exemple. De quel rouge s'agit-il ? Il y a tellement de nuances de rouge. Même question pour le bleu, le vert, le jaune, le magenta, le cyan ! Pour cela il faudrait peut-être se référer aux travaux des biologistes qui ont étudié la sensibilité des cellules rétiniennes en fonction de la longueur d'onde.

Depuis fort longtemps les imprimeurs utilisent la quadrichromie comme procédé d'impression couleur. Ils effectuent une "séparation" en cyan, magenta, et jaune ainsi qu'une image en noir et blanc (plus précisément avec une gamme de gris), ce dernier cliché correspondant aux densités des diverses couleurs; il pourrait être réalisé en utilisant les trois couleurs fondamentales en quantités égales, mais il est plus économique d'utiliser de l'encre noire que de l'encre de couleur. Pour fixer les idées, si une couleur (l'orange décrit plus haut) est définie par \((R, G, B) = (0.60, 0.36, 0.12)\), on a \((C, M, Y) = (0.40, 0.64, 0.88)\); l'imprimeur utilisera la plus grande quantité possible de noir \(N\), c'est-à-dire 0.40, qu'il déduira des couleurs; on aura \((C, M, Y, N) = (0.00, 0.24, 0.48, 0.40)\).

Curieusement, ce n'est que plus tard que les biologistes ont trouvé une explication justifiant ce procédé.

La rétine de notre oeil est tapissée de cellules photosensibles. Il y en a de deux types dénommés cônes et bâtonnets (à cause de leur forme). Il existe trois types de cônes ayant leur maximum de sensibilité chromatique respectivement dans le rouge, le vert et le bleu. Les bâtonnets, quant à eux, sont sensibles aux différences d'éclairement (dans la pénombre les cônes sont quasi inactifs alors que les bâtonnets sont fort utiles). On voit ainsi que notre oeil perçoit également une image en "quadrichromie".

À l'école primaire et dans certaines écoles de dessin, on enseigne que les couleurs fondamentales sont le jaune, le bleu et le rouge. Cela peut s'expliquer par le fait que s'il est vrai que le jaune est une des couleurs fondamentales, le bleu doit en fait être du cyan (bleu verdâtre) et le rouge doit être du magenta (rouge violacé). Il s'agit donc d'une approximation assez grossière de la réalité.