Sur la photo ci-contre, nous observons sur le mur, une jolie figure lumineuse: une hyperbole. Elle est dessinée par la lumière projetée par le lampadaire cylindrique.

Le contour hyperbolique est obtenu par la projection, à partir de l'ampoule, des deux cercles qui limitent les bords supérieur et inférieur de l'abat-jour; comme l'ampoule est située au centre, la lumière émise est formée des deux nappes d'un cône de révolution. En idéalisant quelque peu la situation réelle, on peut dire qu'on a là, la projection d'un cercle à partir d'un point.

Si le lampadaire était tenu à bout de bras horizontalement, nous verrions sur le mur un cercle lumineux; en redressant le lampadaire, ce cercle deviendrait d'abord ellipse, puis parabole et finalement hyperbole.

La transformation qui se passe sur le plan du mur est appelée une projectivité. L'étude des projectivités conduit à la notion de plan projectif.

La linéarité la plus parfaite est obtenue dans l'espace projectif.
Comment définir un espace projectif ? En dehors d'une voie algébrique, deux présentations sont possibles.

1. L'espace projectif en tant qu'espace affin complété par des points "à l'infini" parfois appelés "impropres" (pourtant ils ne sont pas malpropres, il suffit de bien les laver!)
   
2. L'espace projectif construit à partir d'un espace vectoriel.
   

Cette deuxième approche est plus moderne, mais moins intuitive. Les points de l'espace projectif sont les sous-vectoriels à une dimension de l'espace vectoriel, les droites sont les sous-vectoriels à 2 dimensions et ainsi de suite. Cette vision est intéressante lorsque les espaces vectoriels ont été étudiés et elle permet de définir simplement les coordonnées homogènes. Puisqu'on a très (ou trop) souvent l'habitude de travailler avec des coordonnées, cette approche peut être assez utile.

Pourtant, la vision d'un espace projectif en tant qu'espace affin complété par des points est très proche de la démarche historique de Desargues et bien plus intuitive. En gros, on part d'un espace affin et on le complète par ses "points à l'infini". Il est évidemment regrettable que des propriétés de l'espace doivent être énoncées avec des exceptions: par exemple, dans un plan, deux droites se coupent toujours en un point, sauf si elles sont parallèles. Ou bien encore: dans un espace à 3 dimensions, étant donné un plan et un point extérieur, tout plan passant par ce point coupe le plan donné en une droite à l'exception d'un seul appelé parallèle.

Ces exceptions disparaissent lorsqu'on ajoute des points à l'infini et alors, dans un plan, deux droites distinctes sont toujours sécantes en un point, éventuellement à l'infini. De même, dans un espace à 3 dimensions, deux plans distincts se coupent toujours en une droite, éventuellement à l'infini. Lorsqu'on essaie de préciser, un point à l'infini est le point commun à l'ensemble des droites parallèles à une direction. Une droite à l'infini est définie par deux points à l'infini: deux directions de parallèles déterminent un ensemble de plans parallèles à ces deux directions; ces plans ont tous en commun cette droite à l'infini.
Une étape reste nécessaire à franchir: oublier l'expression "à l'infini" et traiter les points et droites ajoutés comme les autres points et droites. On obtient ainsi un espace projectif. Il y a des points, des droites, des plans; dans un plan deux droites distinctes se coupent toujours en un point et, à 3 dimensions deux plans distincts se coupent toujours selon une droite.

Cette approche était celle suivie à la Renaissance, en particulier par les peintres. C'est à cette époque que la perspective est étudiée avec soin, notamment par Dürer, et tout naturellement les points à l'infini apparaissent dans les gravures et les peintures. Une étude très approfondie de la perspective se trouve également chez Vredeman De Vries.

Les transformations projectives diffèrent des transformations affines. Tout comme elles, les relations de linéarité sont conservées, mais le fait d'avoir ajouté des points à l'espace affin, entraîne quelques différences importantes. Deux droites parallèles se projettent généralement selon deux droites sécantes. La figure transformée d'un parallélogramme est un quadrilatère quelconque.
Malgré ces différences, une propriété essentielle subsiste: le birapport (rapport des rapports de section) d'un quaterne (deux couples) de points et en particulier, dans le cas où ce birapport vaut -1; dans ce cas le quaterne est harmonique (généralisation de la notion de milieu quand un des points est à l'infini).

Pour s'habituer aux projectivités, nous vous conseillons de commencer par l'espace projectif à 2 dimensions, le plan projectif. Un petit appareil, fort simple à construire, vous permettra de visualiser les propriétés fondamentales du plan projectif.

Le principe est d'obtenir une projection centrale, c'est-à-dire à partir d'un point, d'une figure. A priori, il n'y a aucune difficulté: on dessine la figure et on la projette à partir d'une source lumineuse ponctuelle. Hélas, lorsqu'on projette un point, le rayon lumineux ne forme en fait qu'une demi-droite. Pour obtenir la droite entière, il suffit de disposer une figure symétrique de la première par rapport à la source lumineuse. Cela est réalisé dans l'appareil décrit ci-dessous.
Il se compose essentiellement d'un support formé de 4 parois et ouvert aux deux extrémités avec une source lumineuse disposée au centre. Il y a intérêt à ce que le support ne soit pas trop allongé, le plus cubique possible afin d'avoir un grand angle de dispersion de la lumière.
Aux extrémités, prévoir soit des glissières, soit des supports pour pouvoir placer des caches. Elles doivent être placées symétriquement par rapport à l'ampoule; pratiquement, les caches sont identiques mais placées en faisant tourner l'une de 180° par rapport à l'autre.

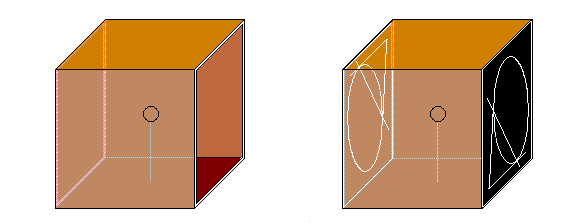
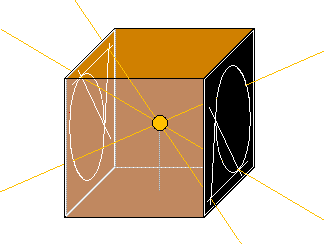
Conseil technique: la manière la plus simple de réaliser ce modèle est d'utiliser comme source lumineuse une ampoule pour torche; l'inconvénient est la faible luminosité. On renforce évidemment la luminosité en utilisant une ampoule quartz-iode mais dans ce cas, il faut tenir compte de la forte chaleur dégagée, prévoir des ouvertures d'aération (qui ne peuvent pas laisser passer la lumière) et utiliser des matériaux résistant à la chaleur.
Quelle que soit la méthode utilisée, il est bon de prévoir une poignée pour pouvoir manipuler l'appareil aisément.

Quelques types de caches intéressants:

		On savait déjà que par projection parallèle (ombre au soleil) un carré pouvait devenir un parallélogramme: le parallélisme est conservé. A présent, la projection centrale d'un carré peut être un quadrilatère quelconque.
		La projection d'un parallélogramme et de ses diagonales est un quadrilatère quelconque. Les diagonales se coupaient en leur milieu, mais à présent, ce n'est plus vrai. On peut également s'amuser à envoyer l'une des diagonales à l'infini; qu'obtient-on alors ?
		Dans un quadrilatère quelconque, les paires de cotés opposés se coupent; par projection centrale, on peut s'arranger pour que leurs points d'intersection se projettent "à l'infini". Alors, les paires de côtés opposés deviennent parallèles et le quadrilatère est un parallélogramme. Les diagonales se coupent alors en leur milieu. Au passage, remarquons que la construction du conjugué harmonique reste valable.
		La projection du cercle est une conique. En inclinant le projecteur peu à peu, le cercle s'étire et devient une ellipse. Rien de neuf, c'était déjà le cas avec l'ombre d'un cercle. Si l'on continue à incliner le projecteur, l'ellipse s'allonge de plus en plus et devient une parabole (du moins on peut l'imaginer) et si l'on continue le mouvement du projecteur, surprise! on voit arriver une deuxième partie de l'image qui est en réalité une hyperbole.
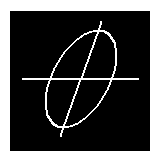
		On peut à nouveau, en manipulant le projecteur, obtenir une conique: ellipse, parabole, hyperbole, au choix. A présent, on constate que ni le centre (de symétrie) ni les diamètres (ensemble des milieux de cordes parallèles) ne sont conservés.
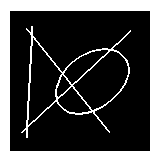
		Un triangle autopolaire d'une conique est conservé (il s'agit de points conjugués harmoniques). Si le côté non sécant est projeté à l'infini, on obtient une ellipse et deux diamètres conjugués. Si c'est l'un des deux autres côté qui s'en va à l'infini, c'est une hyperbole.
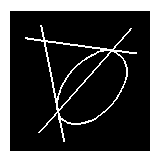
		En envoyant à l'infini une tangente, on obtiendra une parabole munie d'une tangente et du diamètre conjugué. Si c'est la corde des contacts qui s'en va à l'infini, on obtient une hyperbole; l'image des deux tangentes est alors formée des deux asymptotes.

Arrêtons là, mais on peut évidemment songer à de nombreuses autres caches.

Voila revues, avec quelques images mouvantes, les propriétés projectives principales du plan projectif et de ses coniques. On constate ainsi que l'essentiel des propriétés des coniques est de nature projective. Le fait que les figures utilisées se déforment à volonté, facilite grandement la mémorisation de toutes ces notions.