Etant donnés trois points alignés \(\boldsymbol {a, b, c}\), on peut leur associer un nombre, le rapport de section \(\boldsymbol{ca/cb}\). Ce nombre est un invariant pour les projections parallèles, mais non pour les projectivités (par exemple les projections centrales)

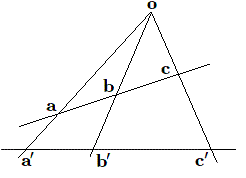
On peut toujours par composition d'une translation et d'une projection centrale (ou parallèle) amener un triple aligné sur un triple aligné. Pour définir un invariant projectif il est dès lors indispensable de considérer plus de trois points.

Si \(\boldsymbol{a, b, c, d}\) sont quatre points alignés, on définit le birapport (appelé également rapport anharmonique) comme le quotient des deux rapports de section de \(\boldsymbol c\) et \(\boldsymbol d\) sur \(\boldsymbol {ab}\):

\[ \boldsymbol{\frac{ca}{cb} / \frac{da}{db}} \]

Ce nombre réel est invariant par projection centrale et constitue donc un invariant projectif. Si l'on utilise des coordonnées et que l'on désigne par \(a, b, c, d\) les abscisses des 4 points \(\boldsymbol{a, b, c, d}\), on a:

\[ \large{r= \frac{\frac{c-a}{c-b}}{\frac{d-a}{d-b}}} \]

Par la structure même de cette expression, et comme il s'agit de quotients de rapports de section, on voit qu'elle est invariante pour les affinités qui appliquent \(x\) sur \(ax + b\) ; un calcul élémentaire montre qu'elle est également conservée par l'application qui envoie \(x\) sur \(1/x\). En groupant ces deux résultats, on voit que le birapport \(r\) est invariant pour les transformations homographiques, projectivités, qui appliquent \(x\) sur \((ax + b)/(cx + d)\).

Géométriquement, cette invariance correspond à l'invariance par projection centrale. En effet soient les 4 points \(a , b, c , d\) alignés sur \(D\) et une projection à partir de \(s\) sur une droite \(D'\) en les points \(a', b', c', d'\).

On peut d'emblée écarter le cas où \(D\) et \(D'\) sont parallèles, ainsi que celui où le centre \(s\) de projection est à l'infini. Dans ces deux cas l'invariance est une simple conséquence du théorème de Thalès. Considérons le cas d'une projection à partir d'un point \(s\) de \(D\) sur \(D'\) non parallèle.

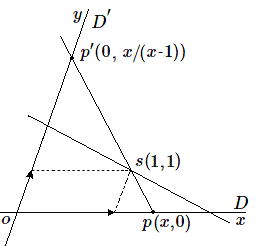
Si on choisit \(D\) et \(D'\) comme axes coordonnés et le point \(s\) comme point \((1, 1)\), on vérifie immédiatement que le point \(p\) de coordonnées \((x, 0)\) est projeté sur le point \(p'\) de coordonnées \((0, x/(x - 1))\).

Cette transformation est décrite par une fonction homographique et il en résulte que le birapport est invariant. Remarquons qu'il est possible, par projection centrale, d'envoyer un point, par exemple \(d\), à l'infini. Dans ce cas le birapport se ramène au rapport de section. En particulier si \(d\) est à l'infini et \(c\) au milieu de \(ab\), le birapport des quatre points vaut -1.

Lorsque 4 points ont un birapport égal à -1 , on dit qu'ils forment un quaterne harmonique.

Algébriquement leurs coordonnées vérifient \(r= \frac{c-a}{c-b}/\frac{d-a}{d-b} = -1\) ou encore: \(\frac{c-a}{c-b}+\frac{d-a}{d-b}=0\) ce qui se ramène à:

\[(a + b)(c + d) = 2(ab + cd)\]

Cette relation, appelée relation d'harmonie est manifestement symétrique en \(a\) et\(b\), en \(c\) et \(d\) et en les paires \(ab\) et \(cd\); on voit ainsi qu'elle exprime que deux paires de points sont conjuguées l'une par rapport à l'autre.

On dit qu'un point \(d\) d'une paire est conjugué harmonique par rapport au point \(c\) de la paire par rapport à l'autre paire \(ab\).

Envisageons quelques cas particuliers, et tout d'abord celui où \(d\) est infini; en divisant les deux membres par \(d\), et en tenant compte du fait qu'un réel divisé par l'infini vaut 0, il vient \(a + b = 2c\) ou :

\[ c =\frac{a+b}{2}\]

Le point \(c\) est le milieu du segment \(ab\), le nombre \(c\) est la moyenne arithmétique des nombres \(a\) et \(b\).

Supposons à présent que d est à l'origine, c'est-à-dire que \(d\) est nul; la relation d'harmonie devient: \((a + b)c = 2ab\) ou \(2/c = (1/a + 1/b)\) ce qui peut s'écrire:

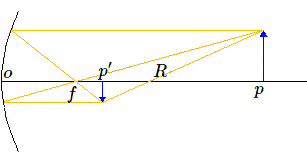
\[ 1/c = \frac{1/a + 1/b}{2} \]

En fait, le nombre \(c\) est la moyenne harmonique des deux nombres \(a\) et \(b\). (C'est la moyenne qui est, ou devrait, être utilisée pour calculer la vitesse moyenne). Remarquons qu'en posant a = p, b = p' et c = R = 2f, la relation devient:

\[ 1/p + 1/p' = 1/f \]

ce qui est la loi des miroirs sphériques étudiée en optique.

Enfin, un autre cas intéressant est celui où l'origine se trouve au milieu de \(c\) et \(d\). On a \(d = -c\) et la relation s'écrit: \(0 = (ab-c^2)\) ce qui est équivalent à:

\[ c = \sqrt{ab} \]

Le nombre \(c\) est alors la moyenne géométrique de \(a\) et \(b\).

Remarquons enfin que l'on en déduit immédiatement la propriété des trois moyennes (classiques) de deux nombres positifs \(a\) et \(b\); la moyenne arithmétique est supérieure à la moyenne géométrique qui est supérieure à la moyenne harmonique; ceci résulte de la position du conjugué harmonique \(c\) de \(c\) par rapport aux deux points \(a\) et \(b\) lorsque \(d\) est à l'infini, sur la partie négative de l'axe, et en l'origine.

Si l'on prend le conjugué harmonique de l'infini par rapport à \(1\) et \(0\), on obtient la moyenne \(1/2\); en prenant le conjugué de \(1\) par rapport à \(1/2\) et \(0\) on obtient \(1/3\), et ainsi de suite: le conjugué de \(1/(n - 1)\) par rapport à \(1/n\) et \(0\) est \(1/(n + 1)\).

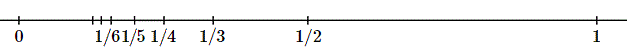
La suite des termes \(1, 1/2, 1/3,...\) ainsi obtenue est appelée suite harmonique et le terme harmonique est liée à la théorie musicale .