La méthode de dessin qui rend le mieux compte de la réalité est ce qui s'appelle la perspective vraie (par opposition à la perspective cavalière et autre perspective militaire). En fait il s'agit d'une projection centrale , ou conique, sur un plan comme le ferait un appareil photographique idéal. Bien entendu par une projection centrale certains points seront projetés à l'infini, mais par contre des points à l'infini seront projetés à distance finie.

Les règles de la perspective, bien que fort simples, n'ont été vraiment mises au point qu'à la Renaissance et c'est l'artiste allemand Dürer qui en a le premier codifié les lois. On s'en convaincra en regardant les tableaux des "primitifs" où la taille des personnages et objets est plus fonction de leur importance que de leur proximité.

De nouveau nous supposerons connue la perspective (projection) d'un trièdre, mais il faudra cette fois préciser où se projettent les points à l'infini des axes coordonnés. Cela correspond au fait qu'une projectivité sur une droite est donnée par les images non plus de deux points mais bien de 3 points, dans notre cas l'origine, le point unité et le point à l'infini. Pour ne pas embrouiller les choses nous nous limiterons à représenter la perspective d'un plan, et pour cela plus précisément la perspective d'un quadrillage. Si nous arrivons à tramer le plan par un quadrillage aussi serré que nécessaire nous saurons dessiner l'image de toute figure tracée dans le plan.

Soient \(o, a, b, x\) et \(y\) respectivement l'origine, les extrémités des vecteurs unités et les points à l'infini des axes. Deux parallèles seront représentées par deux droites se coupant sur la droite de l'infini; toutes les parallèles à une même direction seront représentées par toutes les droites passant par un même point à l'infini (point de fuite). L'ensemble des points de fuite (points à l'infini) sera la ligne d'horizon (droite à l'infini), dans notre cas la droite \(xy\). Le carré construit sur \(boa\) s'obtient aisément; il suffit de mener par \(a\) (resp. \(b\)) la parallèle à \(ob\) (resp. \(oa\)); le quatrième sommet est \(c\).

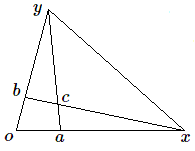
Voyons à présent comment construire le carré \(aced\) adjacent au carré initial. Le point \(e\) est sur la droite \(bc\) que nous connaissons; il est également sur la diagonale \(ae\) qui est parallèle à la diagonale \(oc\). Il suffit donc de tracer \(oc\), et ensuite par \(a\) la parallèle, c'est-à-dire la droite ayant même point à l'infini. En répétant l'opération on obtient ainsi un quadrillage du plan.

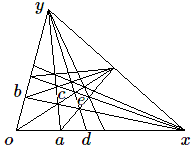
Le réseau des droites ainsi construites est parfois appelé "réseau de Möbius ".

Comment raffiner le quadrillage? Il y a un moyen fort simple de partager un carré en quatre; on trace les diagonales et par leur point de rencontre on mène les parallèles aux côtés, c'est-à-dire les médianes. Voyons comment se fait cette perspective. L'image du milieu \(m\) du segment \(oa\) est déterminée en perspective dès que l'on connaît les positions de \(o, a\) et du point à l'infini \(x\).

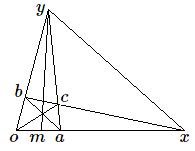
On aurait pu choisir un parallélogramme quelconque \(oac'b'\) et le point \(m\) aurait été le même; la construction de \(m\) est indépendante du point \(y\). On dit que \(m\) est le conjugué harmonique de \(x\) par rapport à \(oa\). Sachant dédoubler une échelle on peut ainsi par dédoublements successifs approcher un point quelconque de la droite, et par suite du plan.

Dès que l'on sait représenter en perspective un plan, avec un peu de soin (et beaucoup de patience) on peut alors représenter en perspective une figure quelconque; un point sera enserré dans une maille cubique aussi petite que l'on veut, et chaque face du cube ne sera autre que la perspective d'un carré.

Les propriétés conservées par perspective ou projection centrale, projection conique, sont les propriétés projectives.

Nous étudierons plus loin les coniques qui sont bien évidemment conservées par perspective; l'outil essentiel sera donc la notion de conjugué harmonique .