A l'occasion de l'étude des projections orthogonales, nous avons utilisé le fait que si un point est l'orthocentre d'un triangle, chacun des sommets du triangle est l'orthocentre du triangle formé par les 2 autres sommets et l'orthocentre de l'ancien triangle.

On peut obtenir une très jolie démonstration vectorielle de cette propriété. Soient \(a, b, c, d\), 4 points quelconques ; on a :

\[ab.cd + ac.db + ad.bc = 0\]

En effet en introduisant un point arbitraire \(p\) on a :

\[(pb - pa).(pd - pc) + (pc - pa).(pb - pd) + (pd - pa).(pc - pb) = 0\]

Cette relation est une identité : si les 4 points \(a, b, c, d\) sont alignés, elle est appelée relation de Stewart.

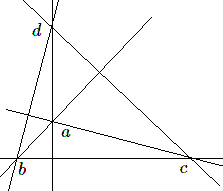
Lorsque les 4 points sont situés dans un plan, on voit que pour un triangle ayant 3 des points comme sommets (par exemple \(a, b, c\), si le point \(bd\) est à l'intersection de deux hauteurs, par exemple \(cd\), la hauteur relative à \(ab\) et \(bd\) celle relative à \(ac\), les deux premiers produits scalaires sont nuls.
Il en résulte que \(ad.bc = 0\) et par conséquent \(ad\) est la hauteur relative au côté \(bc\). Le point d est donc l'orthocentre du triangle abc. On a donc la propriété remarquable :

Etant donné 4 points d'un plan, si l'un est l'orthocentre du triangle formé par les 3 autres, chacun des points est l'orthocentre du triangle ayant pour sommets les trois autres

Remarquons enfin que cette relation ne suppose pas que les 4 points \(a, b, c, d\) soient coplanaires ; on peut en déduire que si dans un tétraèdre \(abcd\), 2 paires de côtés opposés, par exemple \((ab, cd)\) et \((ac, db)\) sont orthogonales, alors il en est de même pour la troisième paire \((ad, bc)\).