Il est évident que si on utilise une axonométrie quelconque on est, en général, choqué par la représentation obtenue. Examinons, à titre d'exemple, la représentation la plus usuelle, la perspective cavalière, et regardons comment se représente une sphère.

Établissons tout d'abord les équations d'une telle projection. Le point de coordonnées \((x, y, z)\) est représenté par le point \((X, Y) = (x - kz, y - kz)\) où \(k\) représente un rapport de réduction sur l'axe \(z\) (dans la pratique \(k\) vaut souvent soit \(½\), soit \(\sqrt{2}/2\)

Soit la sphère \(x^2+y^2+z^2=R^2\). Une famille de plans parallèles au plan \(oxy\) sectionnera la sphère selon des cercles dont les centres s'échelonnent sur l'axe \(oz\) ; chacun de ces cercles se projettera en vraie grandeur et l'image de la sphère sera l'enveloppe de la famille des cercles.

On a:

La sphère d'équation \(x^2+y^2+z^2=R^2\) donne \((X + kz)^2 + (Y + kz)^2 + z^2 = R^2\)

c'est-à-dire: \[ (2k^2 + 1)z^2 + 2k(X + Y)z + X^2 + Y^2 - R^2 = 0 \]

Pour chaque valeur de z on a bien un cercle. Toutefois on ne doit prendre en considération que les points \((X, Y)\) correspondant à des valeurs réelles de \(z\) ; il faut donc que l'équation du second degré en \(z\) admette des racines réelles. On a donc:

\[ k^2(X + Y)^2 - (2k^2 + 1)(X^2 + Y^2 - R^2) \ge 0 \] ou \[ - (k^2 + 1)(X^2 + Y^2) + 2k^2XY + R^2(2k^2 + 1) \ge 0 \]

c'est-à-dire l'équation de l'intérieur d'une ellipse; cette ellipse est l'enveloppe des cercles et les 2 cercles de rayon nul (réduits à un point) sont les foyers de celle-ci.

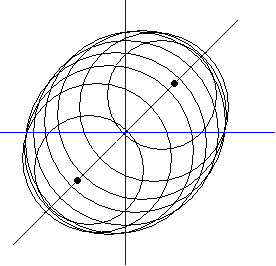
Il est gênant de voir une sphère représentée par une ellipse; on s'attendrait plutôt à un cercle. Cela est dû au fait que la projection que nous utilisons n'est pas une projection orthogonale sur un plan.

Quand on regarde à une distance suffisamment grande un objet de petite taille, on peut assimiler l'image sur la rétine à une projection orthogonale sur un plan; d'où la question: "Comment caractériser les trièdres plans qui sont projection orthogonale d'un trièdre orthonormé ?"

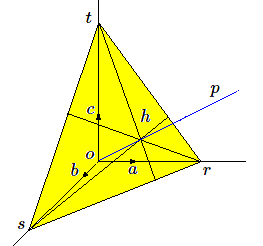Soit un trièdre orthonormé \(oabc\) et \(p\) la projetante passant par \(o\). Sur les axes coordonnés, nous choisirons le sens des vecteurs unités \(oa,  ob,  oc\) de manière à ce que la droite \(op\) soit intérieure à l'angle solide formé par les vecteurs unités.

Un plan perpendiculaire à \(p\) coupe respectivement les axes coordonnés \(oa, ob, oc\) en \(r, s, t\). Le point de percée \(h\) de \(p\) dans ce plan est l'orthocentre (point de rencontre des hauteurs) du triangle \(rst\). En effet, \(rs\) est dans un plan perpendiculaire à \(op\) et à \(oc\); le plan \(ohc\) est donc perpendiculaire à \(rs\), et \(ht\) est donc une hauteur du triangle \(rst\). Nous concluons donc que les supports des 3 vecteurs du trièdre orthonormé se projettent sur les 3 hauteurs d'un triangle.

À présent se pose la question de savoir si 3 droites quelconques concourantes en h peuvent être considérées comme les 3 hauteurs d'un triangle. Partons d'un point quelconque de l'une d'elles et traçons-lui la perpendiculaire; celle-ci rencontre les deux autres droites en \(r\) et \(s\); les 2 perpendiculaires menées de \(r\) et \(s\) concourent en \(t\), situé sur la troisième droite, car \(t\) est l'orthocentre du triangle \(hrs\). On remarque là une propriété intéressante liant les trois sommets d'un triangle et son orthocentre .

Ce point étant acquis, nous voyons que 3 droites concourantes peuvent toujours être considérées comme les trois hauteurs d'un triangle. De plus, nous avons choisi les vecteurs unités de façon à ce que l'orthocentre \(h\) soit intérieur au triangle \(rst\); le triangle \(rst\) ne peut donc pas avoir d'angle obtus; les angles obtus formés par les paires de hauteurs doivent être tels que la réunion des secteurs donne le plan tout entier.

Il reste à déterminer la projection des points unités sur chacun des trois axes. Pour cela, dessinons un triangle \(rst\) dont les trois droites données sont les hauteurs et construisons le développement de la pyramide \(orst\) en faisant pivoter chacune des 3 faces latérales \(ors\), \(ost\) et \(otr\) le long des côtés du triangle rst . Nous obtenons un schéma du type dessiné ci-dessous

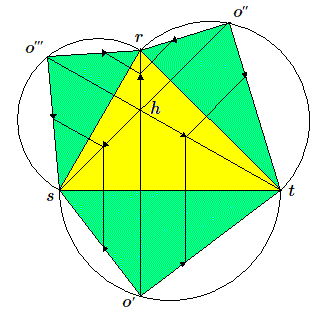
Sur chacun des côtés \(st, tr, rs\) on a un triangle rectangle en \(o\); de plus les 3 triangles \(sto', tro'', rso'''\) se replient en \(o\) (qui se projette sur \(h\)) et par conséquent les points \(o', o''\) et \(o'''\) sont situés sur les hauteurs du triangle \(rst\). Maintenant que le développement est construit il ne reste qu'à reporter des longueurs égales (unités) sur chacun des côtés et à les rabattre sur les hauteurs.

En résumé, il suffit de connaître les directions des projections des trois vecteurs \(oa, ob, oc\) pour reconstituer le trièdre orthonormé.

Signalons que si les trois directions forment des angles égaux (= 120°), les projections des vecteurs unités ont toutes trois même longueur et la perspective est dite isométrique.