Étant donné une fonction \(f(x)\), nous noterons \(f^{(n)}\) la dérivée d'ordre \(n\) de \(f\). Une équation différentielle est dite d'ordre \(n\) si elle ne contient pas de dérivées d'ordre supérieur à \(n\) ; elle sera linéaire si elle peut s'écrire sous forme d'une combinaison linéaire des dérivées: \[ a_n(x)f^{(n)} + a_{n-1}(x)f^{(n-1)} + ... +a_2(x)f'' + a_1(x)f' + a_0(x)f = g(x) \]

Si elle est effectivement d'ordre \(n\), on pourra tout diviser par \(a_n\) et obtenir une forme plus simple. Si la fonction g est nulle, l'équation sera dite homogène (à rapprocher des coordonnées homogènes ). Prenons quelques exemples pour l'ordre \(1\), linéaire et homogène : \[ f' +a_0(x)f = g(x) ~~~~~~ \text{et} ~~~~~~ f' +a_0(x)f = 0\]

La deuxième équation ne paraît pas trop compliquée ; on en déduit \(f'/f=-a_0(x)\). Il reste à calculer la primitive de la fonction \(a_0(x)\) et on obtient \(\mathbf{ln}f=-\int{a_0}(x)dx+k\). Quant à la première équation, elle est moins simple. Prenons alors un cas particulier ; si \(a_0=0\) alors on a \(f=\int g(x)dx + k\). On constate que dans les deux cas, les plus simples, on est ramené au calcul d'une primitive d'une fonction ce qui n'est possible que dans des cas très particuliers ; en effet le résultat n'est généralement pas exprimable par les fonctions usuellement connues !

On serait tenté d'abandonner. Pourtant, en physique, la résolution d'équations différentielles est une question essentielle qui se pose dans la plupart des domaines : mécanique, calorimétrie, électro-magnétisme, etc. La variable \(x\) est généralement le temps \(t\) et le physicien connaît la variation (la dérivée) de la fonction qu'il étudie lorsque le temps varie.

Nous nous limiterons à une classe plus restreinte d'équations différentielles rencontrées en physique, les équations homogènes à coefficients constants , c'est-à-dire quand tous les coefficients \(a_i(x)\) sont des constantes et que la fonction g(x) est nulle.

Introduisons un élément \(D\) défini par \(D=\frac {d}{dx}\). Il s'agit d'un opérateur différentiel qui applique toute fonction de la variable \(x\) sur la fonction dérivée ; on a \(Df=\frac {df}{dx} = f'\). On peut définir \(D^2\) : formellement \(D^2=\frac {d^2}{dx^2}\) et, appliqué à une fonction \(f(x)\), on a: \[ Df= \frac {df}{dx} = f' ~~~~~~\text{et}~~~~~~ D^2 f=\frac {d^2f}{dx^2}=f'' \]

On peut procéder de même pour les dérivées d'ordre supérieur et on aura \(D^n f= \frac{d^n}{dx^n}=f^{(n)}\).

Cette notation nous permet d'associer à toute équation différentielle homogène à coefficients constants une équation algébrique. Par exemple à \[ a_nf^{(n)} + a_{n-1}f^{(n-1)} + ... +a_2f'' + a_1f' + a_0f =0 \]

notée \[ a_nD^nf + a_{n-1}D^{(n-1)}f + ... +a_2D^2f + a_1Df + a_0f =0 \]

que nous pouvons formellement écrire : \[ (a_nD^n + a_{n-1}D^{(n-1)} + ... +a_2D^2 + a_1D + a_0)f =0 \] et que nous pouvons associer à une équation algébrique en l'inconnue X : \[a_nX^n + a_{n-1}X^{(n-1)} + ... +a_2X^2 + a_1X + a_0 =0\]

Cette dernière forme est l' équation algébrique associée à l' équation différentielle .

Pour le premier ordre, l'équation est \(f'+af=0\) avec \(a\) constant ; l'équation algébrique associée est \(X+a=0\) et sa solution est \(X=-a\). Les solutions de l'équation différentielle dépendent d'une constante et sont \(\mathbf{ln}f=-ax+k\) ou plus simplement \(f=Ke^{-ax}\).

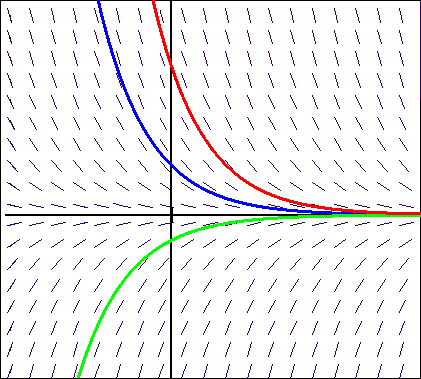Dans le cas où \(a=1\), le schéma ci-contre représente en chaque point la pente \(f'\) du vecteur tangent. On peut constater que la pente de la fonction \(f\) vaut \(-f\) et est indépendante de \(x\).

Les solutions de l'équation \(f'+f=0\) sont représentées par les courbes tangentes en tout point aux vecteurs tangents. Elles sont déterminées par le choix d'un seul de leurs points et dépendent donc d'une constante.

Passons à l'ordre \(2\) ; l'équation homogène s'écrit \(a_2 f''+ a_1 f'+ a_0 f=0\) avec \(a_2 \ne 0\). Réécrivons l'équation homogène \(f''+ pf'+ qf = 0\). On obtient l'équation algébrique associée: \(X^2 + pX + q=0\). Cette équation du second degré possède deux solutions, éventuellement confondues ou imaginaires conjuguées. Si une des solutions est \(a\), on vérifie sans peine que \(e^{ax}\) est solution de l'équation différentielle.

Si l'équation possède deux racines distinctes \(r_1, r_2\) on obtient en combinant linéairement les deux familles de fonctions correspondantes \(Ke^{r_1x}+Le^{r_2x}\).

Remarque: ce résultat reste valable lorsque les deux solutions de l'équation algébrique sont distinctes qu'elles soient réelles ou complexes conjuguées. Si on n'aime pas manipuler des exponentielles complexes, on peut utiliser la formule d'Euler : \(e^{i\omega}=\mathbf{cos~}\omega + i\mathbf{sin}~\omega \) et la solution peut s'écrire \(e^{\rho}(K\mathbf{cos~}\omega + L\mathbf{sin~}\omega)\).

Il reste le cas ou l'équation du second degré possède une solution double \(r\). On a évidemment les solutions \(f=Ke^{rx}\) mais il manque des solutions ! Entêtons-nous et posons \(f(x)=K(x)e^{rx}\) où cette fois \(K\) n'est plus une constante, mais une fonction de \(x\). Exprimons que \(f(x)\) est bien solution de l'équation \(f''+pf'+qf=0\).

Calculons les dérivées de \(f(x)\). On obtient \(f'(x)=(K'+rK)e^{rx}\) et \(f''(x)=(K''+2rK'+r^2 K)e^{rx}\).

L'équation différentielle \(f''+pf'+qf=0\) devient: \[ (K''+2rK'+r^2K)e^{rx}+p(K'+rK)e^{rx}+ qKe^{rx}=0\]

En regroupant les termes, on obtient: \[ (K''+K'(2r+p)+K(r^2+pr+q))e^{rx}=0 \]

Comme \(r\) est solution de \(x^2+px+q=0\) le coefficient de \(K\) est nul. De plus comme c'est une solution double, on a \(2r=-p\). Le coefficient \(2r+p\) de \(K'\) est donc également nul et il ne reste que \(K''=0\). On en conclut que \(K(x)\) est une fonction linéaire \(Lx+M\). La solution générale dépend bien de deux constantes et vaut \((Lx+M)e^{kx}\).

Les résultats obtenus ci-dessus se généralisent sans peine pour les équations à coefficients constants homogènes d'ordre supérieur.

Terminons par un mot sur la résolution d'une équation différentielle à coefficients constants, non plus homogène, mais linéaire. On remarque que si deux fonctions \(f_1\) et \(f_2\) sont solutions d'une même équation linéaire, en soustrayant membre à membre, \(f_1 - f_2\) est solution de l'équation homogène correspondante. Il suffit donc de découvrir une solution particulière de l'équation linéaire ; toutes les solutions de l'équation linéaire s'obtiennent alors en lui ajoutant la solution générale de l'équation homogène.