Dans le premier article consacré aux graphiques de fonctions , nous avons choisi des exemples de fonctions d'une variable \(x\) ne contenant pas de racines carrées.
Nous allons ici considérer quelques fonctions simples \(y = f(x)\) où \(f(x)\) contient la racine carrée d'une fonction de \(x\).
Commençons par un exemple :
\[y = \sqrt{ax² + bx +c}\]Nous connaissons bien les propriétés et le graphique de la fonction du 2e degré. On distingue essentiellement 3 cas :
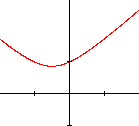
- le discriminant est négatif : \(b² - 4ac < 0\). Aucune valeur de \(x\) n'annule le trinôme \(ax² + bx +c\) ; il conserve toujours son signe. Si \(a < 0\), il n'y a pas de solution réelle ; si \(a > 0\), il y aura un graphique que nous regarderons dans un instant.
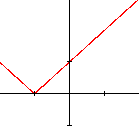
- le discriminant est nul ; \(b² - 4ac = 0\). Le trinôme peut alors s'écrire \(a(x-\alpha)^2\). Si a est négatif, il n'y aura aucune racine réelle à l'exception de \(x =\alpha\), valeur pour laquelle \(y = 0\). Par contre, si \(a\) est positif, le graphique est formé de deux demi-droites se coupant au point de coordonnées \(( \alpha, 0)\)
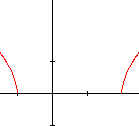
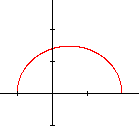
- le discriminant est positif : \(b² - 4ac > 0\). Deux valeurs de \(x\) annulent le trinôme et ce dernier sera positif à l'extérieur de ces valeurs si \(a > 0\) ou positif entre ces valeurs si \(a < 0\). Il y aura donc deux types de graphiques.
Nous donnons ci-dessous 4 graphiques correspondant à 4 types de trinômes.
1)
|
2)
|
3)
|
4)
|
Passons ces 4 cas en revue.
- lorsque x est très grand, le terme le plus important est le terme en x² et la racine carrée vaut soit - x, soit + x ; le graphique possède deux asymptotes obliques de pente ± 1.
- les deux demi-droites ont pour équations \(y = \pm(x + 1)\).
- le graphique est situé à l'extérieur de l'intervalle [-1, +2] et à nouveau il possède 2 asymptotes obliques de pente ± 1.
- le graphique est situé à l'intérieur de l'intervalle [-1, +2].
Enfin, dans les cas 3 et 4, on vérifie qu'aux points x = -1 et x = +2, les tangentes sont verticales (la dérivée est infinie).
Mais réfléchissons un instant.
Nous connaissons les nombres complexes et là, tout nombre possède deux racines carrées opposées (sauf 0 qui a deux racines carrées confondues). Mais on ne peut plus parler de racine positive ! Par exemple les racines carrées de -1 sont \(i\) et \(-i\), mais \(i\) n'est ni positif, ni négatif . Peut-être, serait-il alors intéressant d'étudier l'ensemble des deux fonctions :
\(y = \sqrt{ax^2 + bx +c}\) ainsi que \(y = - \sqrt{ax^2 + bx +c}\)On obtient alors :
1)
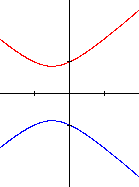
|
2)
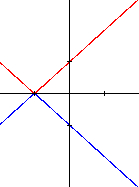
|
3)
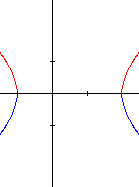
|
4)
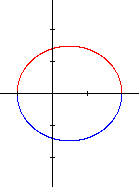
|
Il semble qu'on reconnaisse alors une hyperbole, deux droites sécantes, une autre hyperbole et enfin une ellipse.
Effectivement, il n'est pas compliqué de vérifier cela. Prenons l'équation générale d'une conique, c'est-à-dire un polynôme du 2e degré en les variables x et y. Soit l'équation générale :
\[ax^2 + 2bxy + cy^2 + 2dx + 2ey + f = 0\]en ordonnant par rapport à y, on obtient :
\[cy² + 2(bx + e)y + (ax² + 2dx + f) = 0\]et en résolvant par rapport à y, on obtient selon le signe choisi deux fonctions :
\[y = - (bx + e) ± \sqrt{\frac{(bx + e)² - c(ax² + 2dx + f)}{c}}\]c'est-à-dire une fonction linéaire : \(y = - (bx + e)\), dont le graphique est une droite à laquelle on ajoute (ou retranche) la racine carrée d'un trinôme du 2e degré dont le graphique est du type de l'un de ceux que nous venons de rencontrer.
Prenons un exemple :
\[y = - x + 1 \pm \sqrt{- x² - x + 2}\]Tout d'abord, les graphiques de chacune des deux fonctions.
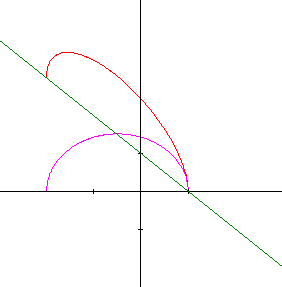
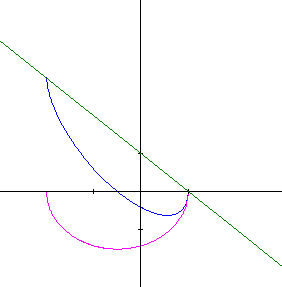
Sur les deux graphiques, on a tracé en vert la droite \(y_1 = - x + 1\) et en violet \(y_2 = \sqrt{- x² - x + 2}\) sur le premier et \(y_2 = - \sqrt{- x² - x + 2}\) sur le second. La somme de ces deux fonctions est dessinée en rouge sur le premier et en bleu sur le deuxième.
Dessinons à présent ces deux fonctions sur un même graphique :
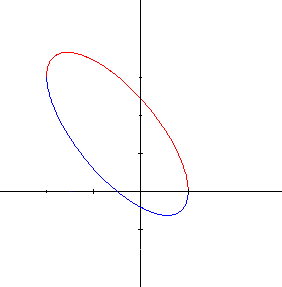
et nous obtenons celui de \(y = - x + 1 \pm \sqrt{- x^2 - x + 2}\) que l'on peut encore écrire sous la forme :
\[(y + x - 1)^2 = - x^2 - x + 2\]On reconnaît mieux ainsi l'équation d'une conique ; on peut encore l'écrire sous forme d'un polynôme du 2e degré en x et y :
\[2x^2 + 2xy + y^2 - x - 2y - 1 = 0\]Terminons par une remarque.
De même que \(y = ax + b\) représente une droite, mais qu'inversement toutes les droites ne sont pas représentées par une équation de ce type (il manque les droites d'équation \(x = a)\), une équation du type \(y = - (bx + e) ± \sqrt{[(bx + e)² - c(ax² + 2dx + f)]/c}\) représente une conique, on n'obtient pas l'ensemble de ces coniques. Si \(c = 0\), la conique s'écrit \(y = - (ax² + 2dx + f)/2(bx + e)\) à condition que \(b \text{ et }e\) ne soient pas simultanément nuls. L'étude des coniques sous forme de fonctions n'est pas bien adaptée à ce problème.
Prenons un autre exemple, la "célèbre" fonction :
\[y = \sqrt{x^2 (x + 1)}\]Son graphique se présente ainsi :
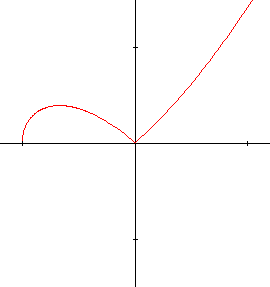
Nous avons dit "célèbre", car c'est presque toujours la fonction donnée en exemple d'une fonction pour laquelle les dérivées à gauche et à droite de l'origine existent mais sont différentes. En effet, lorsqu'on calcule cette dérivée, on est amené à extraire la racine carrée de x². Elle vaut x lorsque x est positif et -x quand x est négatif.
Comme dans le premier cas étudié, le graphique de cette fonction serait plus harmonieux si on le complétait par celui de sa "sœur siamoise" (en prenant l'autre racine carrée) et considérons l'ensemble des deux fonctions :
\[y = \pm \sqrt{x^2 (x + 1)}\]Dessinons cette fois, les 2 fonctions dans la même couleur et nous obtenons :
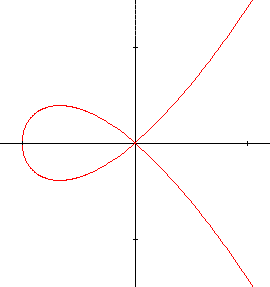
N'est-ce pas bien plus joli ?
Nous sommes maintenant en présence d'une belle courbe, nommée strophoïde, avec une tangente donc la pente varie de manière parfaitement continue. Nous avons perdu le caractère "fonction" (on dit pourtant qu'il s'agit d'une fonction multiforme) et cette courbe représente les points de coordonnées \((x, y)\) tels que \(y = \pm \sqrt{x²(x + 1)}\) ce qui est équivalent à \(y² = x²(x + 1)\) ou encore le graphique de la courbe :
\[x^3 + x^2 - y^2= 0\]Il s'agit d'une courbe du 3 e degré qui est coupée par une droite en au plus 3 points. En particulier, il est intéressant de regarder les intersections avec les droites passant par l'origine. Chacune de ces droites la coupe en deux points confondus à l'origine et un troisième qui varie en fonction de la pente de la droite. Soit l'équation \(y = \lambda x\) d'une droite passant par l'origine. On obtient les abscisses des intersections en remplaçant dans l'équation de la courbe \(y\) par \(\lambda x\) ; cela conduit à :
\[x^3 + x^2 - \lambda^2 x^2= 0 \text{ ou encore } x^3 + (1 - \lambda^2)x^2 = 0\]On observe deux solutions confondues en \(x = 0\) et une 3 e solution \(x = \lambda² - 1\). Cela conduit aux équations paramétriques fort simples de cette courbe :
\[ \begin{cases} x = \lambda^2 - 1 \\ y=\lambda^3 - \lambda \end{cases}\]À propos des tangentes à l'origine, que peut-on en dire ? En valeur absolue, les points de la courbe voisins de l'origine ont des coordonnées \(x\) et \(y\) fort petites (certainement plus petites que 1 !) ; évidemment \(x^2\) et \(y^2\) sont encore plus petits et x³ et y³ encore plus petits. Éliminons les termes les plus petits et au voisinage de l'origine, la courbe est donc très proche de \(x^2 - y^2 = 0\) ou encore \((x + y) (x - y) = 0\). Les deux tangentes sont donc \(y = x\) et \(y = -x\).