Lors de l'envoi des premières sondes spatiales , (Lunik 1, Lunik 2, ...), le problème des transmissions à (très) longue distance s'est posé de manière aiguë. En effet, jusqu'alors les transmissions radio ne dépassaient guère quelques milliers de kilomètres, et les stations émettrices disposaient de toute la puissance nécessaire.
Dans les missions spatiales, les distances étaient bien plus importantes et on était limité (par le poids) en ce qui concernait la puissance des émetteurs. Dès lors il fallait trouver le moyen de pallier aux erreurs inévitables de transmission.
Les informations recueillies sont transmises par des signaux binaires (0 ou 1), mais des erreurs sont possibles. Il faut donc pouvoir les détecter , et mieux encore pouvoir les corriger.
Une manière, pas très maligne, consiste à redoubler chaque signal; si on reçoit 0,0 ou 1,1 tout est en ordre, mais par contre 0,1 ou 1,0 ne peut provenir que d'une erreur. Mais comment la corriger ?
Si on détriple chaque signal, cela devient possible; 1,1,1 ou 0,0,0 est correct (ou alors il y a du y avoir 3 erreurs consécutives) par contre tout autre signal est du à une erreur de transmission. Si on reçoit par exemple 0,1,1 il est clair qu'il y a eu une erreur; en écartant l'hypothèse fort improbable de 2 erreurs, on corrige le signal en 1,1,1. Cela résout le problème de la détection et de la correction d'erreurs, mais quel gaspillage ! On a alors recherché d'autres méthodes.
Nous allons décrire une très jolie solution du problème de détection et correction d'erreur.
Partons d'un cube, et introduisons des coordonnées . Il serait logique d'utiliser le centre du cube comme origine et les trois directions d'arêtes comme directions des axes coordonnées.
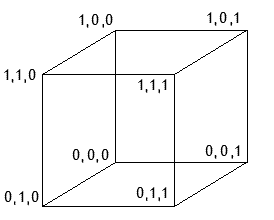Toutefois nous allons procéder autrement. Choisissons un des sommets du cube comme origine et les trois arêtes par ce sommet comme axes coordonnés, et l'arête comme unité. Les 7 autres sommets ont leurs 3 coordonnées non simultanément nulles et égales à 0 ou 1. Nous pouvons définir sur ces 7 sommets un ensemble de triples tel que 2 sommets déterminent un triple qui est déterminé par 2 quelconques de ses éléments.
Comment procéder ?
En général (nous verrons qu'il y a une exception) deux des 7 sommets déterminent avec l'origine un plan qui contient un troisième sommet. Il est évident que de triple de sommet est déterminé par 2 quelconques. Prenons quelques exemples:
les sommets \((0,1,0)\) et \((0,0,1)\) déterminent le sommet \((0,1,1)\) les sommets \((1,0,1)\) et \((1,0,0)\) déterminent le sommet \((0,0,1)\) et ainsi de suite...
D'une manière assez simple il suffit d'additionner les coordonnées des deux premiers sommets pour obtenir celles du troisième avec la règle \(1+1=0\) (songez à impair + impair = pair). Autrement dit, cela revient à travailler modulo 2.
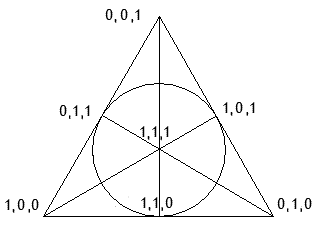
Venons-en à l'exception: les sommets \((1,1,0)\) et \((0,1,1)\) déterminent avec l'origine un plan qui ne contient pas d'autre sommet ! Qu'importe. Utilisons la règle constatée précédemment et additionnons les coordonnées, nous obtenons \((1,0,1)\) et on vérifie que ce triple est déterminé par 2 quelconques de ses éléments. Nous avons ainsi construit sur les 7 sommets du cube une structure linéaire de 7 points munie de 7 droites, où toutes les droites ont trois points.
Nous sommes maintenant en mesure de construire un code.
Il s'agira d'un ensemble de mots qui constitueront le langage utilisé dans une transmission; chaque mot est constitué de lettres qui sont 0 ou 1. Tout mot différent sera le résultat d'erreurs et on supposera qu'il n'y a pas plus d'une erreur possible. Numérotons les sommets du cube de 1 à 7 de la manière suivante:
\(1,0,0\) est le sommet \(1\) \(0,1,0\) est le sommet \(2\) \(0,0,1\) est le sommet \(3\) \(1,1,0\) est le sommet \(4\)
A ce moment nous voyons que les points 1, 2, 4 sont situés sur une droite; supposons que par permutation circulaire nous obtenons les autres droites: 2,3,5 est une droite; dès lors
\(0,1,1\) est le sommet \(5\) et ainsi de suite \(1,1,1\) est le sommet \(6\) \(1,0,1\) est le sommet \(7\).
Nous allons représenter chaque droite en indiquant 1 sur les points utilisés et 0 sur les autres; on obtient:
pour la droite formée des points \(1, 2, 4\):
\(1 1 0 1 0 0 0\)pour la droite \(2, 3, 5\) on a:
\(0 1 1 0 1 0 0\)On obtient ainsi \(7\) mots de \(7\) lettres.
Adjoignons-y le mot formé de tous des \(0\) ainsi que les complémentaires obtenus en remplaçant les \(0\) par des \(1\) et les \(1\) par des \(0\). On obtient finalement les \(16\) mots qui définiront notre code :
0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 1 0 0 0 0 0 1 0 1 1 1 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0 1 1 0 1 1 1 1 0 0 1 0 1 0 0 0 1 1 0 0 1 1 1 0 0 1 0 1 0 0 0 1 1 1 0 1 1 1 0 0 1 0 1 0 0 0 1 0 1 0 1 1 1 0
Sur les \(2^7=128\) mots de \(7\) lettres que l'on peut construire à l'aide des lettres \(0\) et \(1\), il n'y en a que \(16\) qui font partie du code.
Maintenant, c'est un simple exercice de vérifier que deux mots diffèrent par au moins \(3\) lettres. Il en résulte que non seulement nous pouvons détecter une erreur, mais nous pouvons également la corriger.
Il suffit de remarquer que si \(x_1, x_2, x_3, ...\) désignent respectivement la première, la deuxième, la troisème ... lettre du mot, on a toujours:
$$ \begin{align} & x_3 + x_5 + x_6 + x_7 = 0, \\ & \text{ainsi que:} \\ & x_4 + x_6 + x_7 + x_1 = 0, \\ & x_5 + x_7 + x_1 + x_2 = 0, \end{align} $$et les conséquences de ces 3 équations. Si ces équations ne sont pas satisfaites, il y a erreur et suivant la valeur du second membre on en déduit quelle est la lettre erronée du mot transmis.
Donnons un exemple: supposons avoir reçu le mot \(0 1 1 1 1 0 1\). Il ne figure pas dans notre code. On calcule le second membre des 3 équations et on obtient respectivement \(1, 0, 1\). Il y a donc eu une erreur de transmission. La seule manière de corriger une seule lettre est de modifier la cinquième lettre; on obtient ainsi le mot: \(0 1 1 1 0 0 1\) qui fait partie du code.