Il peut être utile, dans certains problèmes relatifs aux polyèdres réguliers , d'utiliser comme outil les coordonnées. Il importe dès lors de bien les choisir, de manière à simplifier au maximum les calculs.

Le choix de l'origine ne pose guère de problème: tout polyèdre possède un unique centre (attention, pour le tétraèdre ce n'est pas un centre de symétrie !); c'est le point fixé par toutes les isométries conservant le polyèdre. Restent à trouver les 3 directions des axes coordonnés orthogonaux.

Le cas le plus simple est celui du cube (ou de son dual l'octaèdre); les 3 directions sont celles des arêtes (des diagonales). En choisissant convenablement l'unité, les coordonnées des 8 sommets du cube seront \((\pm 1,\pm 1,\pm 1)\); (pour l'octaèdre les 6 sommets auront chacun deux coordonnées égales à \(0\) et une égale à \(\pm 1\)).

Passons au tétraèdre. Si l'on considère le symétrique du tétraèdre par rapport à son centre on obtient un second tétraèdre; l'ensemble de ces \(2\) tétraèdres forme un solide que Kepler appelait "Stella octangula"; les huit sommets sont ceux d'un cube, d'où la solution au problème des coordonnées. Il suffit de prendre les points \((\pm 1,\pm 1,\pm 1)\) avec un nombre pair de signes "-".

Restent le dodécaèdre et son dual l'icosaèdre. Remarquons tout d'abord que l'on peut inscrire un cube dans un dodécaèdre; partons d'une diagonale de face du cube et faisons lui subir, ainsi qu'à ses transformées, toutes les rotations d'1/3 de tour autour d'axes passant par le centre du cube et une de ses extrémités (et de celles de ses transformées).

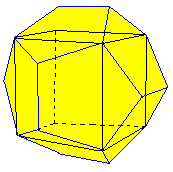
On obtient ainsi les \(12\) arêtes d'un cube; le sous-groupe engendré par cet ensemble de rotations est le groupe du tétraèdre Alt(\(4\)) qui est évidemment un sous-groupe des déplacements du dodécaèdre qui est, lui, isomorphe à Alt(\(5\)) (Remarquons au passage que Alt(\(5\)) contient \(5\) sous-groupes Alt(\(4\)); on peut inscrire au total \(5\) cubes dans le dodécaèdre; à raison de \(8\) sommets par cube cela fait \(40\) sommets répartis sur les \(20\) sommets du dodécaèdre, ce qui donne 2 cubes par sommet; cela correspond au fait que par un sommet passent \(2\) triples de diagonales de face).

Partons à présent d'un cube que nous représenterons ici comme déterminé par les 8 sommets de coordonnées \((\pm 1,\pm 1,\pm 1)\). Pour transporter ce cube, attachons-lui une poignée parallèle aux arêtes d'une face; afin de pouvoir changer de main, fixons-en une autre sur une face adjacente. Continuons, pour l'esthétique, sur chacune des faces et disposons les régulièrement (en fait prenons l'orbite sous l'action du sous-groupe Alt(\(4\)) fixant chacun des 2 tétraèdres inscrits dans le cube).

Nous obtenons en fin de compte un solide limité par \(12\) faces qui sont des pentagones (peut-être gauches, peut-être non réguliers). Soient \((a,0,b)\) avec \(a\gt0, b\gt0\) les coordonnées d'un sommet; l'autre extrémité de la poignée sera \((-a,0,b)\). Exprimons à présent qu'un des pentagones est plan et régulier; par raison de symétrie tous le seront. Les côtés doivent être égaux et valent 2 a ; on obtient:

\[ (a-1)^2+1+(b-1)^2=4a^2 \]

Il faut vérifier si le pentagone est plan: Pour celui représenté sur la figure, il suffit de regarder sa projection sur le plan \(Oxz\): \((a,0,b), (1,0,1)\) et \((b,0,0)\) et de vérifier que ces 3 points sont alignés. Il vient:

\[ a+b^2-2b=0 \]

ce qui nous donne 2 équations à 2 inconnues \(a, b\) :

\[ a+b^2-2b= 0 \\ 3a^2+2a-3-b^2+2b=0 \]

et par addition on arrive à : \(3a^2+2a-3+a=0\) c'est-à-dire \(a^2+a+1=0\) La solution positive est \(a=\tau=1/2(\sqrt{5}- 1)\), b vaut \(1/\tau =1/2(\sqrt{5} + 1)\). Les pentagones sont plans et leurs côtés sont égaux; ce n'est pas suffisant pour qu'ils soient réguliers, mais comme la solution obtenue est unique et que l'on sait que dans un dodécaèdre régulier on peut inscrire un cube, ils sont nécessairement réguliers ! et on obtient ainsi une belle description des 20 sommets: 8 sommets \((\pm 1,\pm 1,\pm 1)\); 12 sommets \((\pm\tau,\pm\tau^{-1},0)\), \((0,\pm\tau,\pm\tau^{-1})\) et \((\pm\tau^{-1},0,\pm\tau)\).

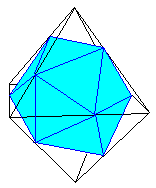La figure duale d'un dodécaèdre est un icosaèdre (20 faces triangulaires équilatérales). La figure duale d'un cube est un octaèdre; il est donc possible d'inscrire un icosaèdre dans un octaèdre. Voyons cela en prenant l'octaèdre dont les sommets ont deux coordonnées nulles et une égale à \({\pm}1\). Sur chacune des 12 arêtes du cube s'appuyait une face du dodécaèdre; dualement sur chacune des 12 arêtes de l'octaèdre se trouve un sommet de l'icosaèdre. Choisissons un point sur une arête: soit \((a,1-a,0)\) ses coordonnées (supposons \(a\gt 0\)); on en déduit facilement les coordonnées des 12 sommets. (C'est l'orbite d'un sommet sous l'action d'Alt(4)).

Exprimons alors que tous les côtés sont égaux: il suffit de considérer le triangle des sommets \((0,a,1-a)\), \((0,a,-(1-a))\) et \((a,1-a, 0)\). On obtient :

\[ a^2+(1-2a)^2+(1-a)^2=4(1-a)^2 \] d'où : \[ a^2+a-1=0 \] et \[ a=\tau=1/2(\sqrt{5} - 1) \]