Voici un petit problème. Des scouts passent près d'une rivière rectiligne ; ils retournent au camp, mais auparavant, ils doivent prendre de l'eau à la rivière. Ils sont fatigués et souhaitent marcher le moins possible. Comment doivent-ils s'y prendre ?

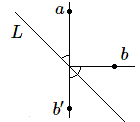Si nous traduisons le problème en termes mathématiques, il faut aller du point \(a\) au point \(b\) en passant par un point de \(L\) de telle sorte que la distance totale soit minimum.

Pour cela prenons le symétrique \(b'\) de \(b\) par rapport à la droite \(L\) et joignons-le au point \(a\). Le trajet de \(a\) à \(b'\) est évidemment minimum et par conséquent celui de \(a\) à \(b\) également. Songeons d'ailleurs à la lumière qui prend également le chemin le plus court (quand on va à près de 300.000 km/sec on n'a pas le temps de faire des détours !). Si on considère \(L\) comme un miroir, on retrouve les lois de la réflexion, l'égalité des angles d'incidence et de réflexion.

Une belle application est la démonstration de la propriété focale de l'ellipse.

Rappelons qu'une ellipse peut être vue comme l'ensemble des points tels que la somme des distances à deux points fixes, appelés foyers, est constante. Mais au fait, pourquoi "foyer"; y a-t-il du feu en ces points ? Nous répondrons à la question dans un instant.

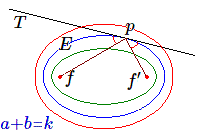Considérons l'ellipse \(E\) et la tangente \(T\) au point \(p\). Si les distances de \(p\) aux foyers \(f\) et \(f'\) valent respectivement \(a\) et \(b\), tous les points de \(E\) satisfont à la relation \(a+b=k\); pour les points intérieurs \(a+b\lt k\), pour les points extérieurs \(a+b\gt k\).

Comme \(T\) est une tangente, on voit que le point \(p\) minimise la distance du trajet de \(f\) à \(f'\) via \(T\). On en conclut qu'il y a égalité des angles formés par les rayons focaux et la tangente (ou la normale).

Cette propriété permet de répondre à la question posée plus haut sur le terme "foyer". Si on imagine une source de lumière (chaude) placée en \(f\) et le bord de l'ellipse une surface réfléchissante, tous les rayons émis viendront se réfléchir et se concentrer en \(f'\). Remarquons que, mutando mutandis , cette propriété est valable pour toutes les coniques (songez aux antennes paraboliques).

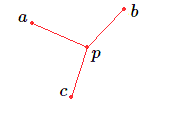
Toujours dans l'esprit de minimiser les trajets, proposons-nous de relier trois points (villes, bâtiments,...). Représentons-les par les trois points \(a,b\) et \(c\) et choisissons un point \(p\) pour tenter de réaliser le réseau minimum au moyen des chemins \(pa\), \(pb\) et \(pc\).

Désignons ces trois distances par \(a, b\) et \(c\).

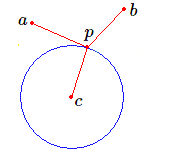Ne modifions pas la distance \(c\) et demandons-nous s'il n'existe pas sur le cercle \(C\) de centre \(c\) un meilleur point \(p'\), c'est à dire un point tel que la somme \(a' + b'\) des distances de \(p'\) à \(a\) et \(b\) soit inférieure à \(a + b\).

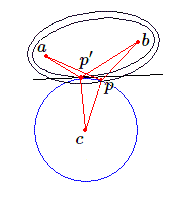
Comme nous le savons les points tels que la somme \(a + b\) est constante sont les points d'une ellipse (de foyers \(a\) et \(b\)). Si nous faisons varier la somme \(a + b\), nous obtenons une famille d'ellipses telle que celle représentée plus haut. Le minimum de \(a+b\) sera atteint lorsque l'ellipse sera tangente au cercle \(C\). Dans ce cas la tangente fera des angles égaux avec \(p'a\) et\(p'b\). Mais cette tangente à l'ellipse est également une tangente au cercle. Il en résulte que \(p'a\) et \(p'b\) sont bissectés par le rayon \(p'c\).

On peut recommencer le raisonnement en partant de deux autres points; il en résulte que chacun des supports des segments bissecte l'angle formé par les deux autres. Les trois segments forment donc entre eux des angles de 120°. Attention ! Nous avons supposé que le point \(p\) était intérieur au triangle formé par les trois autres points, ce qui n'est vrai que si ce triangle n'a pas d'angle supérieur à 120°.

Passons à 4 points, et pour simplifier, supposons qu'ils sont les 4 sommets d'un carré. Comment construire un réseau minimal d'autoroutes reliant ces 4 points ? C'est très simple: par raison de symétrie, il suffit de prendre les deux diagonales du carré.

Eh bien non ! Cela contredirait le résultat précédent.

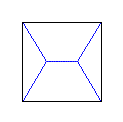
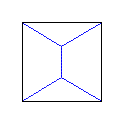
Il n'est guère difficile de voir que la solution n'est pas unique (et c'est là que réside l'erreur qui nous avait fait songer aux diagonales) mais il existe deux solutions formées de 5 segments formant à leur jonction des angles de 120°.

Pour être honnête, cette solution ne s'applique guère en pratique car dans la construction d'autoroutes il faut tenir compte de la configuration du terrain. Par contre elle convient fort bien quand il s'agit de relier 4 bâtiments.