Nous allons décrire un jeu très simple dans ses règles: le pile ou face menteur, une simplification du poker menteur.

Deux joueurs jouent à pile ou face; face gagne et pile perd. Le premier joueur lance la pièce, prend connaissance du résultat, et annonce un résultat à son adversaire qui, lui, n'a pas pu voir la pièce. Le deuxième joueur est donc désavantagé. Pour compenser cela, il a le droit de refuser (comportement R ) l'annonce qui lui est faite et de demander à voir la pièce. S'il accepte (comportement A ) l'annonce du premier joueur, celui-ci gagne 10 € si c'est face et perd 10 € si c'est pile.

Naturellement, dans ces conditions le jeu ne serait pas très amusant; le premier joueur annoncerait systématiquement face, et le second joueur demanderait toujours à vérifier.

On décide donc que s'il demande à vérifier, les enjeux sont doublés; si le premier joueur a dit la vérité (comportement V ), mais est soupçonné à tort de mensonge, il recevra 20 €; par contre s'il a réellement menti (comportement M ), il perdra 20 €

Accepteriez-vous de jouer à ce jeu ? Le jeu est-il équitable ? Un des deux joueurs n'est-il pas avantagé par le règlement? Si oui, comment rendre le jeu équitable? Quelle stratégie adopter? Voilà bien des questions que nous allons envisager.

Tout d'abord remarquons que chacun des deux joueurs peut, à chaque jeu, opter pour deux stratégies. Nous avons donc 4 comportements possibles: ( V , A ), ( V , R ), ( M , A ), ( M , R ); dans chacun de ceux-ci nous allons calculer le gain (ou la perte) moyenne du premier joueur.

Comportement ( V , A ): c'est le jeu de pile ou face usuel; une fois sur deux il gagne 10 €, une fois sur deux il perd 10 €. La moyenne sera nulle, c'est un jeu équitable. Comportement ( V , R ): une fois sur deux le premier joueur tire face et l'annonce; comme le second refuse, on vérifie et le joueur gagne 20 €; une fois sur deux il tire pile et l'annonce; le second joueur serait mal venu de refuser et le premier joueur doit donc payer 10 € à son adversaire. En moyenne, il gagnera 5 €.

Venons-en au comportement de menteur. Comportement ( M , A ): comme le second joueur ne demande jamais à vérifier, le premier gagne 10 € quel que soit le résultat. Comportement ( M , R ): le premier joueur n'annonce évidemment jamais pile; le second demande toujours à vérifier; une fois sur deux il aura raison et le premier perdra 20 €, une fois sur deux il aura tort et le premier joueur gagnera 20 €. Dans ce cas, le jeu se ramène pour le second joueur à un simple jeu de pile ou face (avec mise de 20 €) et il est donc équitable.

Résumons cela dans un tableau à double entrée:

		joueur1
		V	M
joueur2	A	0	10
	R	5	0

Une conclusion saute aux yeux: le premier joueur ne perd jamais. Dès lors mettons-nous à sa place (intéressante !). Comment doit-il jouer ? S'il choisit de mentir ( M ) pour avoir un gain le plus grand possible, le second joueur aura tôt fait de deviner la tactique de son adversaire et dès lors il demandera toujours à vérifier ( R ). Du coup le premier joueur ne gagnera plus rien. Il va donc changer de stratégie et dira la vérité ( V ), mais alors, le second joueur, dès qu'il s'en rendra compte, modifiera lui aussi sa stratégie: il acceptera ( A ) et du coup le premier joueur ne gagnera plus rien. Il va à nouveau modifier sa stratégie, et ainsi de suite. On voit qu'il n'y a pas de position équilibrée: le jeu est donc intéressant.

Comme les joueurs doivent chacun varier leurs stratégies, nous allons donc supposer qu'ils le font avec une fréquence déterminée, mais imprévisible par l'adversaire. Le premier joueur choisira ( V ) avec une fréquence p et, par conséquent ( M ) avec une fréquence (1 - p ). Le second joueur choisira la stratégie ( A ) avec une fréquence q et donc la stratégie ( R ) avec la fréquence (1 - q ).

Ceci étant fixé, calculons le gain moyen du premier joueur en fonction de chacune des stratégies choisies, compte tenu de leur fréquence:

Stratégie	fréquence	gain	gain moyen
( V, A )	\(p.q\)	0	0
( V, R )	\(p(1-q)\)	5	\(5p(1-q)\)
( M, A )	\((1-p)q\)	10	\(10(1-p)q\)
( M, R )	\((1-p)(1-q)\)	0	\(0\)

En résumé, le gain moyen du premier joueur sera:

\[ v=0 + 5 p(1-q) + 10 (1-p).q + 0 \]

Dès que la fonction \(v\) est connue, la stratégie de chacun des joueurs est bien précise et on peut représenter les choses graphiquement. 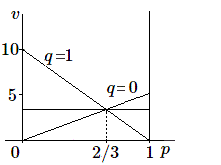Du point de vue du premier joueur, on établit le graphique de son gain \(v\) en fonction de sa stratégie \(p\); il faut bien entendu le faire pour tous les choix possibles de l'adversaire. On établit pour chacune des valeurs de \(q\) le graphique de la fonction \(v=5p+10q -15pq\), \(v\) étant considérée comme fonction de \(p\). On obtient chaque fois une droite.

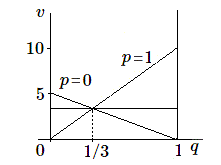La fonction \(v\) peut s'écrire: \(v\)= 5 \(p\) + \(q(10-15p)\) et représente donc le faisceau des droites passant par un même point. (Bien entendu \(p\) ne peut varier que dans l'intervalle \([0, 1]\) et il s'agit en réalité d'un segment). On constate que le premier joueur doit donc choisir \(p = 2/3\), sans quoi un choix astucieux de l'adversaire diminuerait son gain.

Le deuxième joueur agit de même en étudiant \(v\) comme fonction de \(q\) et trouve la valeur \(q = 1/3\). Tout autre choix risquerait d'entraîner une perte plus importante pour lui.

En résumé, les deux joueurs choisissent \(p\) et \(q\) de telle manière que la fonction \(v\) soit maximum pour l'un et minimum pour l'autre quel que soit le choix de l'adversaire; on annule donc les dérivées par rapport à \(v\) et à \(q\) et on obtient le système d'équations:

\[ \partial_p v=~~5-15q=0 \\ \partial_q v=10-15p=0 \]

La solution de ce système donne \(p = 2/3\), \(q = 1/3\): cette solution assure la stabilité du jeu. Pour chacun des deux joueurs la droite représentative de ses gains (ou pertes) est une droite horizontale. Il peut être intéressant de faire un graphique à 3 dimensions de la fonction v des deux variables \(p\) et \(q\). On l'obtient aisément à partir de sections à p constant (droites) et de sections à q constant (droites). La surface obtenue est appelée paraboloïde hyperbolique (ou selle de cheval). (A rapprocher de celle que l'on obtient avec la loi des gaz parfaits).

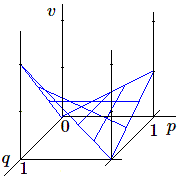
Cette surface possède un point particulier, appelé point de selle, où le plan tangent est horizontal, où l'on est en équilibre. Il est déterminé par deux génératrices horizontales.

Cette figure est à rapprocher du calcul du barycentre des 4 points correspondant aux stratégies pures.

On peut, connaissant le choix des deux joueurs: \(p = 2/3, q = 1/3\), calculer la valeur \(v\) du jeu. On obtient \(v= 5.(2/3) + 10.(1/3) - 15.(2/3).(1/3)\) c'est-à-dire \(v = 10/3\). Le jeu n'est donc pas équitable et le premier joueur gagnera donc en moyenne \(10/3\)€ par partie. Il est donc évident que personne n'acceptera de jouer ce jeu en tant que second joueur(...et pourtant il y a tant de gens qui jouent au Lotto !).

Pour rendre le jeu équitable il faut donc modifier les règles du jeu en diminuant les gains du premier joueur de \(10/3\)€ dans chacune des 4 éventualités.

Cet exemple est un cas très simple de ce que l'on appelle la théorie des jeux. Cette branche des mathématiques s'est développée pendant la guerre de 1940-45 à l'occasion de recherche de stratégies optimales dans divers domaines militaires; transport de troupes et de matériel, manœuvres sur le terrain, etc.

Citons un exemple réel lors de l'avance des troupes alliées après le débarquement en Normandie. Les armées alliées dirigées par le général Omar Bradley étaient face à la 9e armée allemande commandée par le général von Kluge. Celui-ci pouvait soit attaquer vers l'ouest pour tenter de couper les armées alliées, soit battre en retraite vers l'est pour assurer ses positions sur la Seine. Le général Bradley qui commandait les troupes alliées pouvait soit rappeler ses réserves, soit envoyer ses troupes vers l'est pour harceler l'armée allemande ou alors rester sur ses positions pour les consolider et attendre l'arrivée des réserves.

La matrice du "jeu" était la suivante:

		Général von Kluge
		Attaque	Retrait
Général Bradley	Réserve	2	3
	Vers l'Est	1	5
	Attendre	6	4

Seul était pris en compte le degré d'efficacité des différentes stratégies.

On remarque que pour le choix de Bradley la première stratégie est toujours moins bonne que la troisième. On est donc ramené à un jeu de 2 joueurs à 2 stratégies qui n'a pas de point d'équilibre. Toutefois, ce jeu ne se joue qu'une seule fois (!) et dans ce cas, il est logique que chacun des adversaires choisisse de jouer la sécurité en minimisant ses risques de perte: Bradley devait donc attendre ses réserves et von Kluge se retirer; c'est ce qu'ils décidèrent.

Cependant Hitler n'accepta pas la décision de von Kluge et lui donna l'ordre d'attaquer; dès lors Bradley maintint ses positions, les réserves arrivèrent et encerclèrent les troupes allemandes, ce qui conduit von Kluge au suicide.

La morale est-elle sauve ?