Nous connaissons par expérience de nombreuses figures de l'espace et certaines de leurs propriétés. Nous allons reprendre l'étude de celles-ci d'une manière plus rigoureuse. Pour les démontrer, il est indispensable de se baser sur certaines propriétés élémentaires que l'on accepte au départ. Ce sont des axiomes.

Nous étudierons dans cette section quelques propriétés affines de l'espace.

Tout d'abord livrons-nous à quelques observations:

L'espace est un ensemble de points; certains sous-ensembles sont particulièrement intéressants: les droites et les plans. Pour éviter les ambiguïtés, précisons la terminologie utilisée. Deux droites sont dites parallèles si elles sont soit confondues, soit situées dans un même plan et sans point commun. De même deux plans sont dits parallèles s'ils sont soit confondus, soit sans point commun. Enfin deux droites non coplanaires sans point commun sont dites gauches .

Par un point passent plusieurs droites; si nous fixons un deuxième point, nous obtenons une droite unique passant par ces 2 points. Par cette droite passent plusieurs plans; si nous choisissons un point extérieur à la droite, nous obtenons un plan unique contenant la droite et le point. Considérons à présent un plan p et un point extérieur P. Chaque droite de p détermine avec P un plan a. Si la droite se déplace dans le plan p, le plan a varie autour du point P, et inversement, chaque fois que nous prenons un plan passant par P nous aurons une droite dans le plan p. Il y a cependant une exception: il existe un plan passant par P ne rencontrant pas le plan p: c'est le plan parallèle. Nous connaissions déjà cette exception dans le plan: étant donné une droite d et un point extérieur P, toutes les droites du plan passant par P coupent D à l'exception de la parallèle. Prenons à présent deux droites. Elles peuvent être situées dans un même plan; elles sont alors sécantes ou parallèles. Si elles ne sont pas situées dans un même plan, nous dirons qu'elles sont gauches. Soient d et d' deux droites gauches. Un point P situé sur d' détermine avec d un plan d. Si le point P se déplace sur d', le plan d tourne autour de d; à chaque position de d correspondra un point P avec toutefois une exception: il y a un plan passant par d qui ne rencontre pas d'; c'est le plan parallèle à d'.

Rassemblons les principales propriétés rencontrées:

1. Par deux points distincts passe une et une seule droite.
2. Par une droite et un point extérieur passe un et un seul plan.
3. L'intersection de deux plans distincts non parallèles est une droite (ou dès que deux plans distincts ont un point commun ils ont une droite commune).
4. Par un point passe une et une seule droite parallèle à une droite donnée.

Remarque

Les axiomes que nous avons choisis constituent des propriétés simples de l'espace; nous aurions pu en choisir d'autres, par exemple: par trois points non alignés passe un unique plan. Par contre, en ce qui concerne le parallélisme, l'axiome 4 n'est pas équivalent à "Par un point passe un et un seul plan parallèle à un plan donné" (exercice: chercher un contre exemple). Des axiomes ne constituent pas un absolu; ils peuvent être remplacés par d'autres qui leur sont équivalents.

Nous admettrons donc les propriétés 1 à 4 en tant qu'axiomes et, ayant acceptés ces "règles du jeu" sans démonstration, nous les utiliserons pour démontrer d'autres propriétés.

Pour être tout à fait correct, ajoutons un axiome:

5. Les droites comprennent au moins deux points et les plans comprennent au moins trois points non alignés.

Par la suite, pour étudier d'autres propriétés de l'espace, les propriétés métriques, nous serions amenés à introduire des axiomes supplémentaires exprimant les relations entre plans et droites perpendiculaires.

I. Si un plan contient deux points d'une droite, il la contient tout entière.

A et B d A et B π

}

d π

Soit le point P 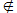π; P et d déterminent le plan π' qui est distinct de π par construction; π et π' ont un point commun; ils ont donc une droite commune (Ax.3); cette droite contient les points A et B; c'est donc la droite d (Ax.1); donc d = π π' d π

II. Par trois points non alignés passe un et un seul plan.

Soient A, B, C trois points non alignés. a) Par A et B passe une droite d (Ax.1); par d et C passe un plan π (Ax.2). Il existe donc un plan passant par A, B et C. b) Supposons qu'il existe deux plans distincts π et π', contenant A, B et C: π π' = i (Ax.3); A, B et C i, donc ils sont alignés, ce qui est contraire à notre hypothèse. Le plan π est donc unique!

III. Par deux droites sécantes passe un et un seul plan.

Soient a et b deux droites et I = a b. a) Soient A a et B b, supposés distincts de I. Les trois points A, B, I déterminent un plan π (Th.II) Le plan π contient A et I, donc π contient a (Th. I) Le plan π contient B et I, donc π contient b (Th. I) b) Ce plan est unique (Application: démontrer par l'absurde que π est unique)

IV. Par un point extérieur à un plan passe un seul plan parallèle.

Soit le plan π et le point P 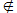π. a) Montrons tout d'abord qu'il y a au plus un plan parallèle. Soient π' et π" deux plans parallèles à π par P. π' et π" ont en commun le point P; ils se rencontrent donc en une droite i (Ax.3). Soit α un plan passant par P, mais pas par i, et rencontrant π. On aurait α π = d , α π' = d' et α π" = d". Dans le plan α on aurait par le point P deux parallèles d et d', ce qui contredirait l'axiome 4. b) Démontrons à présent l'existence de ce plan parallèle; prenons deux sécantes d et d' du plan π. Dans les plans α = (d, P) et α' = (d', P), menons les uniques droites l et l' parallèles à d et à d' (Ax.4). Ces deux droites sécantes en P appartiennent à une unique plan π' (Th.III). Si π π' 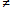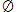; alors soit i = π π' (Ax.3) Cette droite i doit rencontrer soit d, soit d' (Ax.4). Soit Q = d i; Q α , or Q π' ; donc Q l = α π', ce qui contredit le parallélisme de d et l.

V. Par deux parallèles passe un et un seul plan. (Application: le démontrer)

VI. Si trois plans distincts se coupent 2 à 2, leurs intersections sont soit concourantes, soit parallèles 2 à 2, soit confondues.

Soient α, β, γ trois plans et a = β γ, b = γ α, c = α β; a b = (β γ) (γ α) = α β γ De même b c = c a = a b = α β γ Les droites b et c sont contenues dans α; trois cas sont donc possibles: a) b c = {P}: les droites a, b, c concourent en P. b) b c = 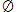: donc c a = a b = 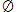; les droites étant situées 2 à 2 dans un même plan, elles sont parallèles 2 à 2. c) b = c: alors a = b = c = α β γ

VII. Toute droite parallèle à une droite d'un plan est parallèle à celui-ci.

Si la droite est contenue dans le plan le théorème est évident. Supposons a//b π ; a 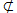π. Soit α le plan (a, b). Comme a α, en coupant par le plan π on obtient a π α π donc il en résulte que a π b. En coupant par la droite a, on obtient a π a b = 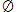, puisque par hypothèse a//b, donc a//π Exercice: le démontrer par l'absurde.

VIII. Etant donné deux droites gauches, par l'une d'elle passe un et un seul plan parallèle à l'autre.

Soient a et b deux droites gauches: a b = 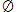. Choisissons P a et désignons par β le plan contenant P et b (Ax.2). Soit b' la droite telle que P b'//b (Ax.4) et α l'unique plan tel que a α et b' α (Th.III). En vertu du Th.VII, b//b' et b' α b//α. Exercice: démontrer l'unicité par l'absurde.

IX. Si deux droites sont parallèles, tout plan coupant l'une coupe l'autre.

Soient a et b les 2 parallèles: elles déterminent un plan π. Soit α un plan quelconque rencontrant a en A d = α π. Si d ne rencontrait pas b, par le point A nous pourrions mener deux parallèles à b, la droite a et la droite d. Les droites d et b se rencontrent en B d α et B α

X. Si deux plans sont parallèles, tout plan coupant l'un coupe l'autre et leurs intersections sont parallèles.

(application: le démontrer par l'absurde)

XI. Deux parallèles à une droite sont parallèles entre elles.

a//d b//d

}

a//b

Nous pouvons supposer que a, b, d ne sont pas dans un même plan. (Dans ce cas la démonstration serait immédiate) Soit α le plan (a, d) et β le plan (b, d). Soit γ un plan passant par a et un point P b, P 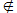d. α, β, γ sont trois plans distincts se coupant 2 à 2. α β = d, α γ = a. Comme a//d, en vertu de la propriété VI, b//a.

XII. Si une droite est parallèle à un plan, tout plan (non parallèle au premier) passant par cette droite coupe le premier plan suivant une parallèle à la droite.

a//π, α π

a α b = α π

}

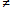
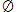
a//b

Si a π, le théorème est évident; supposons donc a π = 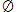et soit {I}= a b.

I a I b π

}

I a π

Mais ceci est contraire à notre hypothèse. Conclusion: Les théorèmes VII et XII nous permettent d'énoncer un critère de parallélisme pour une droite et un plan:

XIII. Pour qu'une droite soit parallèle à un plan, il faut et il suffit qu'elle soit parallèle à une droite de ce plan.

XIV. Deux plans parallèles à un même troisième sont parallèles entre eux. (à démontrer).

XV. Si un plan contient deux droites respectivement parallèles à deux sécantes d'un autre plan, les deux plans sont parallèles, et réciproquement. Les hypothèses sont: a π, b π, a b = {P} a' π', b' π', a'//a, b'//b et la thèse est: π//π' D'après le théorème VII, a//a' a//π' ; de même: b//π' Si π non//π', d'après le théorème XII, π a//π' π π'//a et π b//π' π π'//b Comme a et b sont sécantes, cela contredirait Ax.4 . Donc π//π' On démontrera aisément la réciproque de ce théorème. Conclusion

XVI. Pour que deux plans soient parallèles, il faut et il suffit que l'un contienne deux droites respectivement parallèles à deux sécantes de l'autre.

XVII. Le rapport de section se conserve par projection parallèlement à un plan. ou: Un faisceau de plans parallèles détermine sur deux droites gauches des segments homologues proportionnels (Théorème de Thalès).

Soient d et d' deux droites gauches, α, β et γ trois plans parallèles rencontrant d en A, B, C et d' en A', B', C'. Menons une droite quelconque d" s'appuyant sur d et d'; elle rencontre α, β, γ en A", B", C". Le plan (d, d") coupe α, β et γ suivant trois parallèles. On a: (CA/CB)=(C"A"/C"B") (Théorème de Thalès dans le plan). Le plan (d', d") coupe α, β et γ suivant trois parallèles. On a: (C'A'/C'B')=(C"A"/C"B") Par conséquent: (CA/CB)=(C'A'/C'B') Sur base de la remarque mentionnée en VIII, nous avons admis et utilisé la version plane du théorème de Thalès.

XVIII. L'ensemble des points partageant dans un rapport donné les vecteurs liés ayant pour origine les points d'un plan et pour extrémité ceux d'un plan parallèle est un plan parallèle à ces deux plans. (Réciproque du théorème de Thalès). (A démontrer).

Vecteurs dans l'espace

Tout ce qui a été vu relativement aux propriétés vectorielles du plan reste valable dans l'espace. A titre d'exemple nous résoudrons l'exercice suivant:

Les médianes d'un quadrilatère gauche se coupent en leur milieu.

Soient K, L, M, N les milieux des côtés AB, BC, CD, DA du quadrilatère gauche. Choisissons un point quelconque O. OK = (OA+OB)/2, OL = (OB+OC)/2, OM = (OC+OD)/2, et ON = (OD+OA)/2 Le milieu P de la médiane KM est tel que OP = (OK+OM)/2 = (OA+OB+OC+OD)/4 Le milieu Q de la médiane LN est tel que OQ = (OL+ON)/2 = (OB+OC+OD+OA)/4 Par conséquent P et Q sont confondus et le théorème est démontré.

Exercices de géométrie de l'espace 1°) Déterminer une droite s'appuyant sur 3 droites gauches données. Construire un modèle représentant les trois droites gauches ainsi que quelques droites s'y appuyant. 2°) Etant donnés 5 points tels que 4 quelconques d'entre eux ne soient pas coplanaires, a) combien de droites déterminent-ils deux à deux ? b) combien de plans déterminent-ils trois à trois ? c) combien de ces droites chacun de ces plans contient-il ? d) combien passe-t-il de ces plans par chacune de ces droites ? On coupe la figure formée de ces droites et de ces plans par un plan quelconque. Quelle est la figure obtenue dans de plan de section ? Faire un modèle. 3°) A l'aide de l'exercice 2°), démontrer le théorème de Desargues: si les droites joignant les sommets homologues de 2 triangles sont concourantes, les points d' intersection des côtés homologues sont alignés et réciproquement. 4°) On considère un plan π, deux points fixes A et B, n'appartenant pas à π et un point M variable n'appartenant pas à π. Les droites MA et MB rencontrent respectivement le plan π aux points A' et B'. Montrer que, lorsque le point M varie, la droite A'B' passe, en général, par un point fixe. 5°) Deux droites d et d' se coupent en un point I. Une droite d rencontre en A le plan π = (d, d'). Soient un point M d, et les plans α = (M, d) et α' = (M,d'). Montrer que la droite d' = α α' passe par un point fixe lorsque M décrit d. Quel est l'ensemble des positions de d' ? 6°) Les lettres latines désignent des droites, les lettres grecques des plans, est-il vrai que: l//m, l coupe n m coupe n l//m, l coupe n m non // n l coupe m, m coupe n l coupe n l//m, m coupe n l coupe n l α, α//β l//α l//α, m α l//m l α, l//β α//β α//β, l α, m β l//m ou l coupe m l//m, m//α l//α l coupe α, m α l non//m l//α, l//β α//β l gauche avec m, α//l α coupe m l α, α coupe β, l coupe α β l α, α coupe β, m β l non//m 7°) On considère un plan π et deux droites a et b qui rencontrent ce plan respectivement en A et B. a) Soit M a. La parallèle à b par M rencontre π en M'. Quel est l'ensemble des positions de M' quand M décrit a ? b) Le plan mené par M parallèlement à π rencontre la droite b en N. Quelle est la nature du quadrilatère MM'NN'? 8°) Soient deux plans α et β se coupant suivant d, et un point A n'appartenant ni à α ni à β. On considère deux plans α'//α et β'//β passant par A. a) Que peut-on dire de d' = α β' ? b) Quel est l'ensemble des positions de d' lorsque A décrit une droite d? 9°) Dans l'exercice 2, quelle est la figure obtenue dans le plan de section lorsque celui-ci est parallèle à un des plans déterminés par 3 des 5 points ? Que devient cette figure lorsque, de plus, la droite déterminée par les deux autres points est parallèle au plan de section ? 10°) Généraliser pour un tétraèdre les notions de médiane d'un triangle et de médiane d'un quadrilatère. Montrer que les 7 médianes d'un tétraèdre sont concourantes. Préciser la position de leur point de rencontre. 11°) Etant donné un quadrilatère gauche: a) Démontrer que les droites joignant les milieux des côtés opposés sont concourantes. b) Démontrer que les droites joignant les point et partageant côtés opposés dans un même rapport sont parallèles à un même plan π. il en sera de même pour les droites joignant les points partageant dans un même rapport les deux autres côtés. Soit π' un plan parallèle à la deuxième famille de droites. c) Montrer qu'une droite de la première famille rencontre toutes les droites de la deuxième famille et inversement. d) 0n projette la figure formée par les deux familles de droites parallèlement à i = π π' sur un plan non parallèle à i. Qu'obtient-on ? e) Réaliser le modèle. 12°) On considère 3 axes coordonnés (non coplanaires) Ox, Oy et Oz. Définir les coordonnées (x, y, z) d'un point de l'espace dans un tel repère. Quels sont les ensembles de points définis respectivement par les équations;

x = a, y = b, z = c, ax + by = 0, ax + by = c, ax + by + cz = 0, ax + by + cz + d = 0

Faire un modèle. Interpréter géométriquement la résolution d'un système de 3 équations linéaires à 3 inconnues et discuter les différents cas possibles. 13°) On considère l'ensemble E d'équation z = xy. a) Qu'obtient-on en le coupant par les plans x = constante? b) Qu'obtient-on en le coupant par les plans y = constante? c) Qu'obtient-on en le coupant par les plans z = constante? d) On considère la figure formée par les axes Ox, Oy, les sections de E par un plan x = a et un plan y = b. A l'aide de l'exercice 11, caractériser l'ensemble E. e) Comparer à la loi des gaz parfaits pv = kT et aux lois à pression constante, à volume constant et à température constante. 14°) Démontrer qu'étant donnés 2 triangles OXY et O'X'Y' (2 systèmes d'axes coordonnés) situés dans 2 plans π et π', il est possible de passer par une suite de projections parallèles du premier triangle au second. (On considérera des plans intermédiaires, p.ex. un plan passant par O' et un plan passant par O'X').

Ceci dit, avons-nous fait de la géométrie ?

Tout au mieux, nous avons fait quelques petits exercices de logique. Mais à aucun moment nous n'avons dessiné, ni fait, à deux exceptions près, de petits modèles dans l'espace. Bref nous avons fait de la logique, ce qui n'est pas mauvais, mais il importe de faire également de la géométrie. Nous conseillons d'ajouter pour les nombreuses propriétés démontrées plus haut un petit schéma.

Une alternative à cette étude fort austère est la suivante: Nous proposons quelques petits exercices de dessin dans le plan. (Il n'est malheureusement pas commode de faire en classe des petits modèles tridimensionnels, ce qui serait préférable.) Nous dessinerons les figures dans un dièdre formé des plans α horizontal et β vertical. Nous représenterons en rouge les figures situées dans le plan horizontal et en vert celles situées dans le plan vertical .

Chaque étape de la solution doit être justifiée correctement.

		Trouver l'intersection du plan π déterminé par la droite d et le point P avec le plan horizontal α
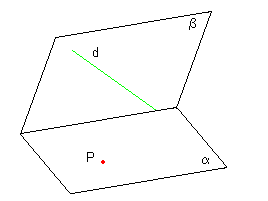
		Trouver l'intersection du plan π déterminé par la droite d et le point P avec les plans horizontaux et verticaux.
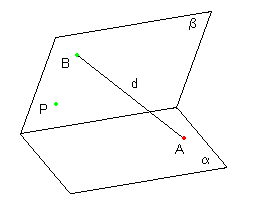
		Trouver l'intersection de la droite PQ du plan π, déterminé par la droite d et P, avec le plan horizontal α
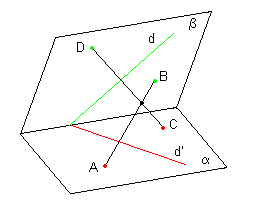
		Trouver l'intersection du plan déterminé par les droites d et d' avec le plan déterminé par les deux sécantes AB et CD.
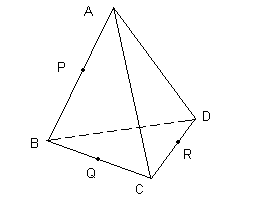
		Dessiner l'intersection du plan PQR avec le tétraèdre ABCD.
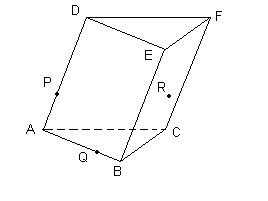
		R est situé dans la face BCEF. Dessiner l'intersection du plan PQR avec le prisme ABCDEF.
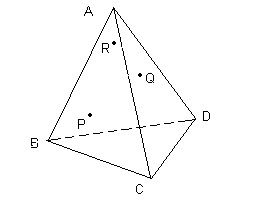
		P est dans le plan ABC, Q est dans le plan ACD et R est dans le plan ABD Tracer l'intersection du plan PQR avec les trois plans ABC, ABD et ACD Terminer en traçant l'intersection de ce plan avec le plan BCD.

Et maintenant ?

Que préférez-vous ?

Si vous n'êtes pas convaincu par la méthode graphique et que vous préférez encore la méthode logique, nous vous donnons comme exercice: "Démontrer la théorème de Desargues". (Il va sans dire qu'il vous est interdit de tracer une figure !).

Bonne chance.

Epilogue

Sommes-nous bien certains d'avoir une bonne axiomatique qui correspond fort bien à nos sensations de l'espace habituel ? Pourtant nous n'avons rien demandé aux droites. Ont-elles un nombre fini ou infini de points ? Si oui, sont-elles ordonnées ?

Eh oui ! Ce n'est pas si simple l'axiomatique.