- Produit scalaire de deux vecteurs - Vecteurs orthogonaux - Repère orthonormé
- Distance de deux points
- Equation normale d'une droite
- Distance d'un point à une droite
- Coefficient angulaire
- Equations paramétriques d'une droite
- Angle de deux droites - condition de perpendicularité
- Rotation du repère - Rotation du plan
- Déplacement des axes - Déplacement du plan
- Cercle - Centre - Rayon - Equations
- Intersection avec une droite - Tangente
- Puissance d'un point par rapport à un cercle - Axe radical
- Angle de deux cercles
- Autres configurations intéressantes
1. Produit scalaire de deux vecteurs - Vecteurs orthogonaux - Repère orthonormé
Soit \(v_1, v_2\) deux vecteurs de coordonnées \((x_1, y_1)\) et \((x_2, y_2)\). Calculons leur produit scalaire en tenant compte de la bilinéarité de ce produit.
\(\begin{align} v_1.v_2 =& (x_1\imath + y_1\jmath).(x_2\imath + y_2\jmath) \\ =&~x_1y_1\imath^2 + (x_1y_2 + x_2y_1) \imath.\jmath + x_2y_2\jmath^2\end{align}\)
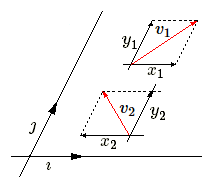Pour calculer cete expression il faut donc connaître \(\imath^2,\jmath^2 \) ainsi que \(\imath.\jmath \), c'est-à-dire le carré de la longueur des vecteurs de base ainsi que leur produit scalaire.
Il sera donc commode, quand il s'agit de traiter des propriétés métriques, de choisir un repère formé de deux vecteurs unités et perpendiculaires.
Le produit scalaire \(\imath.\jmath = 0\) et le carré de leur longueur \(\imath^2 = \jmath^2 = 1 \).
Dans ce cas l'expression du produit scalaire devient:
\( v_1.v_2 = (x_1\imath + y_1\jmath).(x_2\imath + y_2\jmath) = x_1y_1+ x_2y_2 \).Le repère est dit orthonormé. Pour l'étude des propriétés métriques du plan, nous utiliserons toujours un repère de ce type.
2. Distance de deux points
Soit les deux points \(a_1 (x_1,y_1)\) et \(a_2 (x_2,y_2)\). Les coordonnées de \(a_1a_2\) sont \((x_2-x_1, y_2-y_1)\). Si \(\delta\) désigne le module du vecteur, on a: \(\delta^2= {a_1a_2}^2 = (x_2-x_1)^2 +(y_2-y_1)^2\). On a donc :
| \(\delta=\sqrt{(x_2-x_1)^2 +(y_2-y_1)^2}\) |
3. Equation normale d'une droite
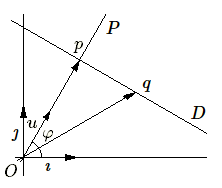Soit une droite \(D\). Menons par l'origine O la perpendiculaire \(P\) à \(D\) désignons par \(p\) le point d'intersection de \(P\) et \(D\). Si \(q\) est un point quelconque de \(D\), on a \(Oq = Op+pq.\) Multiplions scalairement cette égalité par un vecteur unité \(u\) de la droite \(P\) et compte tenu que \(pq\) est perpendiculaire à \(u\), on obtient :
Les coordonnées de \(Oq\) sont \((x,y)\) ; la vecteur \(u\) a pour coordonnées \((\mathbf{cos~}\varphi ,\mathbf{sin~}\varphi)\) où \(\varphi\) désigne l'angle que fait \(P\) avec l'axe \(Ox\) ; \(Op = \mathbf{d}~u\) où \( \mathbf{d}\) désigne la distance de l'origine à la droite. En remplaçant dans la relation ci-dessus, on obtient:
\(x~\mathbf{cos~}\varphi + y~\mathbf{sin~}\varphi =\mathbf{d}\) ou \(x~\mathbf{cos~}\varphi + y~\mathbf{sin~}\varphi - \mathbf{d}=0\)ce qui est appelé l' équation normale de la droite \(D\)
On remarque que la comme des carrés des coefficients de \(x\) et \(y\) vaut \(1\). Pour normaliser l'équation d'une droite \(ux+vy+w=0\), il suffit de diviser par \(\sqrt{u^2+v^2}\)
| \[ \frac{ ux+vy+w}{ \sqrt{u^2+v^2}} = 0\] |
4. Distance d'un point à une droite
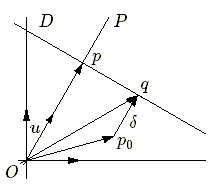Soit la droite \(D\) et le point \(p_0(x_0,y_0)\) et traçons \(p_0q\perp D\). On a
Multiplions les deux derniers membres de cette égalité par le vecteur \(u\) de \(P\). On obtient : \[ Op.u + pq.u = Op_0.u +p_0q.u \]
Compte tenu que \(Op.u=\mathbf{d} \) et que \(pq.u=0\), en remplaçant \(Op_0\) par sa valeur \(x_0~\mathbf{cos~}\varphi + y_0~\mathbf{sin~}\varphi \), on obtient: \[\mathbf{d} = x_0~\mathbf{cos~}\varphi + y_0~\mathbf{sin~}\varphi + p_0q.u \]
Or \(p_0q.u \) est, en valeur absolue, précisément la distance \(\delta \) du point \(p_0\) à la droite \(D\) ; on obtient finalement:
| \( \delta = |~x_0~\mathbf{cos~}\varphi + y_0~\mathbf{sin~}\varphi - \mathbf{d}~| = \Large{|~\frac{ ux_0+vy_0+w}{ \sqrt{u^2+v^2}}~|} \) |
On voit qu'il suffit de remplacer dans le premier membre de l'équation normale de la droite \(x,~y\) par les coordonnées \(x_0,~y_0\) du point \(p\).
5. Coefficient angulaire
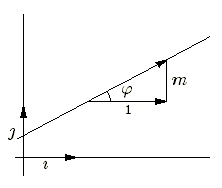Etant donné une droite \( ux + vy + w = 0 \), le ceofficient angulaire \(m = \large -\frac{u}{v} \). Dans un repère orthonormé, \(\large -\frac{u}{v}\)\( = \mathbf{tan~}\varphi \) où \(\varphi \) est l'angle formé par la droite avec l'axe des \(x\). Le coefficient directeur prend alors le nom de coefficient angulaire (ou pente) de la droite.
6. Equations paramétriques d'une droite
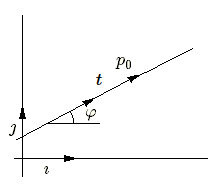Soit une droite, \(D\) faisant un angle de \( \varphi \) avec l'axe \(Ox\), passant par le point \( p_0~(x_0,y_0) \). Un vecteur unité de la droite a pour coordonnées \( (\mathbf{cos~}\varphi , \mathbf{sin~}\varphi) \). Les équations paramétriques de la droite sont donc:
| \( \begin{align} x =& x_0 + t~\mathbf{cos~}\varphi \\ y =& y_0 + t~\mathbf{sin~}\varphi \end{align} \) |
7. Angle de deux droites - condition de perpendicularité
7.1 Angle de deux droites orientées
Soit 2 droites d'équation :
\( D_1 \equiv u_1 x + v_1 y +w_1 = 0 \\ D_2 \equiv u_2 x + v_2 y +w_2 = 0 \)
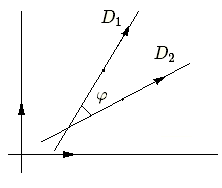Les vecteurs \( d_1 (v_1, -u_1) \) et \( d_2 (v_2, -u_2) \) sont des vecteurs directeurs respectivement de \( D_1 \) et de \( D_2 \).
Le produit scalaire \( d_1.d_2 = | d_1 | | d_2 | \mathbf{cos~}\varphi \) ; par conséquent \( \mathbf{cos~}\varphi = \large \frac{d_1.d_2}{| d_1 | | d_2 | } \). On peut donc écrire :
| \( \mathbf{cos~}\varphi =\Large \frac{u_1 u_2 + v_1 v_2}{\sqrt{u_1^2 + v_1^2}\sqrt{u_2^2 + v_2^2} } \) |
La condition de perpendicularité est tout simplement :
| \( D_1\perp D_2~~\iff~~\mathbf{cos~}\varphi = 0~~\iff~~u_1 u_2 + v_1 v_2 = 0 \) |
7.2 Angle orienté de deux droites
On appelle angle orienté de deux droites \(D_1, D_2\) et on note \((d_1,d_2)\), l'angle dont il faut faire tourner \(D_1\) pour l'amener sur \(D_2\); cet angle est donné à \(\pi\) près.
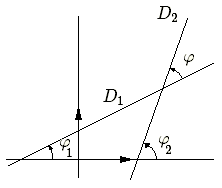Dans ce cas il sera commode de travailler avec les coefficients angulaires \(m_1\) et \(m_2\) des deux droites. Soit \(m_1 = \mathbf{tan~}\varphi_1\) et \(m_2 = \mathbf{tan~}\varphi_12\).
L'angle \(\varphi = (d_1,d_2) = \varphi_2 - \varphi_1\). On a donc : \( \mathbf{tan~}\varphi = \mathbf{tan~}(\varphi_2 - \varphi_1) = \large \frac{\mathbf{tan~}\varphi_2 - \mathbf{tan~} \varphi_1}{1+\mathbf{tan~} \varphi_1 \mathbf{tan~}\varphi_2 } \)
| \( \mathbf{tan~}\varphi = \large \frac{m_2-m_1}{1+m_1m_2} \) |
La condition de perpendicularité est tout simplement :
| \( D_1\perp D_2~~\iff~~\mathbf{tan~}\varphi = \infty~~\iff~~m_1 m_2 = -1 \) |
8. Rotation du repère - Rotation du plan
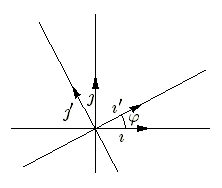Soit un repère \( (\imath, \jmath) \) d'origine O. Considérons le repère \( (\imath', \jmath') \) image du premier par une rotation d'angle \(\varphi\) autour du poin O. On a :
Prenons un point \(p\) de coordonnées \((x,y)\) et calculons ses coordonnées dans le nouveau repère. On a :
\( \begin{align} Op =&~~ x'~\imath' + y'~\jmath'\\ =&~~ x'(\mathbf{cos~}\varphi~\imath + \mathbf{sin~}\varphi~\jmath ) + y' (-\mathbf{sin~}\varphi~\imath + \mathbf{cos~}\varphi~\jmath)\\ =&~~(x'\mathbf{cos~}\varphi~\imath - y'\mathbf{sin~}\varphi)~\imath + (x'\mathbf{sin~}\varphi + y'\mathbf{cos~}\varphi)~\jmath \\ =&~~x~\imath + y~\jmath \end{align} \)Les équations d'un changement de repère seront données par:
| \( \begin{align} x =&~~x'\mathbf{cos~}\varphi - y'\mathbf{sin~}\varphi \\ y =&~~x'\mathbf{sin~}\varphi + y'\mathbf{cos~}\varphi \end{align} \) |
Si on considère ces équations comme liant les coordonnées d'un point \(p(x,y)\) et celles de son transformé \(p'(x',y')\) dans un même repère, on obtient les équations d'une rotation d'un angle \(-\varphi\) autour de l'origine.
9. Déplacement des axes - Déplacement du plan
Un déplacement du plan peut toujours se décomposer en une rotation autour d'un point quelconque suivi d'une translation. On a donc de manière analogue les équations d'un changement de repère en composant les résultats obtenus ci-dessus avec une translation.
| \( \begin{align} x =&~~x'\mathbf{cos~}\varphi - y'\mathbf{sin~}\varphi + x_0\\ y =&~~x'\mathbf{sin~}\varphi + y'\mathbf{cos~}\varphi + y_0\end{align} \) |
Il y a de nouveau une double interprétation :
- soit comme lien entre nouvelles et anciennes coordonnées d'un point après déplacement du repère
- soit comme les coordonnées d'un point et de son transformé par déplacement dans un repère fixe.
10. Cercle - Centre - Rayon - Equations
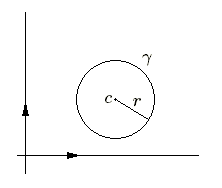Le cercle \(\gamma\) est défini par son centre \(c~(x_0, y_0)\) et son rayon \(r\). Un point \(p~(x,y)\) appartiendra au cercle \(\gamma\) lorsque le carré de sa distance sera égal au carré du rayon.
L'équation vectorielle du cercle sera :
| \(cp^2 = r^2\) |
Le vecteur \(cp\) a pour coordonnées \((x-x_0, y-y_0)\) ; par conséquent l'équation du cercle \(\gamma\) peut s'écrire :
| \( (x-x_0)^2 + (y-y_0)^2 = r^2 \) |
Si le cercle est centré à l'origine des coordonnées l'équation est tout simplement \(x^2+y^2=r^2\). Dans le cas général, l'équation devient : \( x^2 -2x_0x+x_0^2 + y^2 -2y_0y+y_0^2=r^2\).
Réciproquement, étant donné une équation de la forme \( a(x^2+y^2)+2bx+2cy+d=0 \), vérifions s'il s'agit bien d'un cercle en essayant de la ramener à la forme générale. Tout d'abord, il faut évidemment que \( a\neq 0 \) sinon l'équation sera celle d'une droite (si \(b\) et \(c\) ne sont pas simultanément nuls). Dans ce cas divisons par \(a\) et l'équation peut s'écrire sous la forme :
\( (x+\large\frac{b}{a})^2 + (y+\large\frac{c}{a})^2=\large \frac{b^2+c^2-ad}{a^2}\)et l'équation représente un cercle de centre \( c~(-b/a, -c/a) \) de rayon \(r^2=\large \frac{b^2+c^2-ad}{a^2} \). Toutefois, il faut que cette valeur de \(r^2\) soit positive ! On en conclut que cette équation représente un cercle de rayon \(r=\sqrt{\large \frac{b^2+c^2-ad}{a^2}}\) ; au cas où elle est nulle, le cercle est de rayon nul et se réduit à un point et enfin lorsqu'elle est négative, le cercle ne possède aucun point réel.
Lorsque le premier membre de l'équation du cercle est écrit de manière que le coefficient de \(x^2+y^2\) vaut \(1\), l'équation du cercle est écrite sous forme normale .
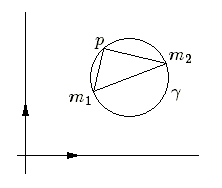Dans le cas où un cercle \(\gamma\) est donné par un diamètre d'extrémités \(m_1~(x_1,y_1)\) et \(m_2~(x_2,y_2)\), pour qu'un point \(p\) appartienne à \(\gamma\), il faut et il suffit que le produit scalaire \(m_1p.m_2p = 0\). Son équation sera donc :
| \( (x-x_1)(x-x_2) + (y-y_1)(y-y_2) = 0 \) |
Le cercle peut être également décrit par des équations paramétriques. Soit \(\varphi\) l'angle du vecteur \(cp\) avec l'axe \(Ox\). Le vecteur \(Op = Oc + cp\) et le module de \(cp = r\). On obtient donc les équations :
| \( \begin{align} x =&~~x_0 + r~\mathbf{cos~}\varphi \\ y =&~~y_0 + r~\mathbf{sin~}\varphi \end{align} \) |
11. Intersection avec une droite - Tangente
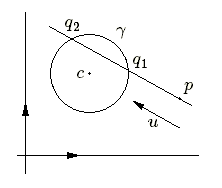Soit le cercle \(\gamma\) de centre \(c\) et de rayon r\(\). Cherchons les poins d'intersection avec la droite \(D\) définie par un de ses points \(p\) et un vecteur unité \(u\). On doit résoudre le système des équations :
Or en remplaçant cq par sa valeur :
\(r^2 = cq^2 = (cp+pq)^2 = (cp +\delta~u)^2 = cp^2 + 2cp~\delta~u + \delta^2~\)et on obtient les valeurs de \(\delta\) ( correspondant aux points d'intersection \(q\) ) données par l'équation:
\(\delta^2+2\delta~u.cp+cp^2-r^2 = 0\)Cette équation du second degré peut avoir, selon les données 2 solutions, une solution double ou aucune solution réelle : cela correspond respectivement aux cas où la droite est sécante, tangente ou non-sécante au cercle. Supposons que le point \(p~(x_1,y_1)\) appartienne au cercle. Dans ce cas \(cp^2=r^2\) et le terme indépendant de l'équation est nul. Une des solution est évidemment \(0\). La droite est sécante ou tangent. Si elle est tangente l'autre solution doit également être nulle et le coefficient du terme du premier degré est nul; autrement dit le produit scalaire \(cp.u=0\) ce qui montre que le rayon cp est perpendiculaire au vecteur u dirigé selon la droite.
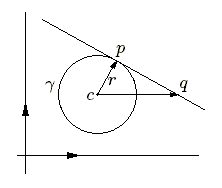Soit \(T\) la tangente au cercle en un point \(p~(x_1,y_1)\). Pour tout point \(q\) de \(T\), \(cq=cp+pq\). Comme \(pq\) est perpendiculaire à \(cp\), le produit scalaire \(cp.cq = cp^2=r^2\).
L'équation vectorielle de la tangente en \(p\) est donc :
| \( cp.cq=r^2 \) |
en remplaçant \(cp~(x_1-x_0, y_1-y_0)\) et \(cq~(x-x_0, y-y_0)\) par leurs coordonnées, on obtient l'équation cartésienne de la tangente :
| \( (x-x_0)(x_1-x_0) + (y-y_0)(y_1-y_0) = r^2 \) |
12. Puissance d'un point par rapport à un cercle - Axe radical
Reprenons l'équation qui donne les points d'intersection d'un cercle de rayon \(r\) avec une droite passant par \(p~(x_1, y_1)\) de direction \(u\). Les valeurs de \(d\) sont données par l'équation
\(\delta^2+2\delta~u.cp+cp^2-r^2 = 0\)On constate que le produit des racines est constant. Quel que soit le vecteur \(u\), c'est-à-dire la direction de la droite, le produit \(P\) des distances du point \(p\) aux points d'intersection \(q_1\) et \(q_2\) est constant et vaut
| \( P =cp^2-r^2 \) |
Cette grandeur \(P\) est appelée puissance du point \(p\) par rapport au cercle \(\gamma\).
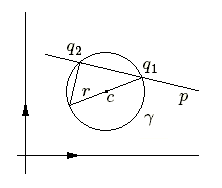L'équation vectorielle \(cp^2-r^2=0\) exprime que le point \(p~(x,y)\) est situé sur un cercle de centre \(c\) de rayon \(r\). La puissance \(P\) d'un point \(p_1~(x_1,y_1)\) s'obtient donc en remplaçant dans l'équation du cercle \(x\) et \(y\) par les coordonnées du point \(p_1\). En coordonnées cartésiennes, la puissance
\(P\) d'un point par rapport à un cercle s'obtient donc en remplaçant \((x,y)\) par les coordonnées \((x_1,y_1)\) du point \(p_1\) dans l' équation normale
du cercle \(\gamma\).
Cette situation est à rapprocher de celle qui donnait la distance d'un point par rapport à une droite.
Etant donné deux cercles, on peut rechercher l'ensemble des points ayant la même puissance par rapport à ces deux cercles. Nous venons de voir que la puissance s'obtient en remplaçant les coordonnées \((x, y)\) par les coordonnées du point \((x_1,y_1)\) dans l'équation normale du cercle. En égalant les puissances, les termes du second degré \((x_1^2+y_1^2)\) vont disparaître et on obtiendra une relation linéaire entre les coordonnées. L'ensemble des points d'égale puissance sera donc une droite appelée axe radical des deux cercles.
13. Angle de deux cercles
Soit deux cercles :
\( \gamma_1 \equiv a_1 (x^2+y^2)+2b_1x+2c_1y+d_1=0 \\ \gamma_2 \equiv a_2 (x^2+y^2)+2b_2x+2c_2y+d_2=0 \)
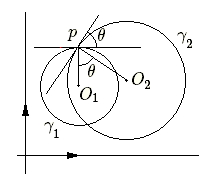L'angle \(\theta\) de deux cercles est, par définition, l'angle formé par les tangentes en leurs points d'intersection. Comme la tangente est perpendiculaire au rayon, si les cercles sont centrés en \(O_1\) et \(O_2\) et que \(p\) un des points d'intersection, l'angle des cercles est égal à l'angle des 2 vecteurs \(pO_1\) et \(pO_2\). Les modules de ces vecteurs sont respectivement égaux à \(r_1\) et \(r_2\) et on a donc \(pO_1.pO_2=r_1.r_2\mathbf{cos~}\theta\).
Pour faire apparaître ce produit scalaire, il suffit de remarquer que \(O_1O_2=O_1p+pO_2\) et de calculer le carré de cette relation:
On en déduit
\(2pO_1.pO_2=pO_1^2+pO_2^2-O_1O_2^2\) ou \(2r_1r_2\mathbf{cos~}\theta=r_1^2+r_2^2-O_1O_2^2\)En remplaçant les coordonnées du centre et la valeur des rayons par leurs valeurs \(o_i=\large(-\frac{b_i}{a_i},-\frac{c_i}{a_i})\) et \(r_i=\large\sqrt{\frac{b_i^2+c_i^2-a_id_i}{a_i^2}}\), on obtient
\(2r_1r_2\mathbf{cos~}\theta=1/2[\large \frac{b_1^2+c_1^2-a_1d_1}{a_1^2}+\frac{b_2^2+c_2^2-a_2d_2}{a_2^2}-(\frac{b_1}{a_1}-\frac{b_2}{a_2})^2-(\frac{c_1}{a_1}-\frac{c_2}{a_2})^2]\)Après de nombreuses simplifications, on obtient
\(2r_1r_2\mathbf{cos~}\theta=\frac{1}{\large a_1a_2}[b_1b_2+c_1c_2-1/2(a_1d_2+a_2d_1)]\)et finalement
| \(\mathbf{cos~}\theta=\Large \frac{b_1b_2+c_1c_2-1/2(a_1d_2+a_2d_1)}{\sqrt{b_1^2+c_1^2-a_1d_1}\sqrt{b_2^2+c_2^2-a_2d_2}}\) |
Cette formule est facile à mémoriser car elle découle de la forme quadratique \(b^2+c^2-ad\) et de la forme bilinéaire associée.
On remarque également que si un ou deux des cercles sont remplacés par des droites la formule reste valable bien que la démonstration ne le soit plus !
14. Autres configurations intéressantes
Nous ne développerons pas ce point. Nous nous bornerons à signaler quelques sujets d'étude intéressants.
L'étude des propriétés de cercles orthogonaux, cercles dont les tangentes aux points d'intersection sont perpendiculaires.
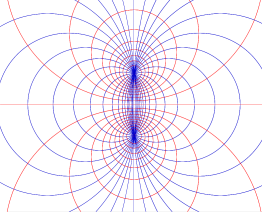
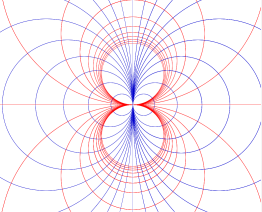
Tout comme on a étudié les faisceaux de droites on peut étudier le faisceaux de cercles. On distingue plusieurs types de faisceaux. Mis à part les faisceaux de cercles concentriques, les cercles peuvent être sécants, tangents ou disjoints. Dans chacun des 3 derniers cas, le faisceau contient une droite qui est l'axe radical commun à toutes les paires de cercles du faisceau.
On peut également étudier l'ensemble des cercles orthogonaux à un faisceau de cercles. On constatera que les cercles orthogonaux à un faisceau de cercles sécants constituent un faisceau de cercles disjoints et réciproquement. S'il s'agit d'un faisceau de cercles tangents, on obtiendra également un faisceau du même type.
|
|