Lors de l'étude des ensembles de nombres, on est amené à utiliser le mot "groupe" à propos des propriétés des opérations qui y sont définies.

Dans les entiers, l'addition a une structure de groupe commutatif; par contre, la multiplication ne possède pas cette structure (on ne peut en général pas diviser). Par contre, dans les rationnels, la multiplication possède, à condition d'exclure 0, une structure de groupe .

De même en géométrie, on utilise également le mot "groupe".

L'ensemble des isométries du plan possède une structure de groupe non commutatif

Voici des phrases qu'on peut lire ou entendre et qui sont livrées aux élèves généralement trop tôt. Dès lors, il n'est pas étonnant que, faute d'une quantité suffisante d'exemples et de contre-exemples, tout cela reste mal compris.

En fait, le terme groupe est utilisé dans deux sens différents. Dans le premier cas, il s'agit de "groupes" (parfois qualifiés d'abstraits) et dans le second, de "groupes de permutations" mais on n'explicite généralement pas la distinction mais aussi les liens entre ces deux notions.

On nous dit que la notion de groupe a été introduite en mathématiques, suite aux travaux d'un génial mathématicien français, Evariste Galois.

Voyons cela de plus près.

Très jeune, Galois s'est intéressé au problème de la résolution d'équations algébriques. On sait qu'il existe certaines fonctions des racines (ou solutions) qu'on peut calculer sans résoudre l'équation. L'exemple classique est celui de l'équation du second degré dont on peut calculer la somme et le produit des racines sans résoudre l'équation; même si, lors d'une première étude sur les réels, on se trouve en présence d'une équation qui ne possède pas de solution ! Ces deux grandeurs S = x ₁ + x ₂ et P = x ₁ .x ₂ sont invariantes si on permute les racines et ne nécessitent donc pas l'identification de chacune d'elles. Quand le degré de l'équation augmente, il y a davantage de fonctions calculables sans résolution de l'équation. Par ailleurs, il y a plus de manières de permuter les racines.

Il arrive que l'équation possède des propriétés particulières; une équation sans terme de degré impair (alors si x ₁ est solution, -x ₁ l'est également), une équation réciproque (si x ₁ est solution, 1/x ₁ l'est aussi),... Dans ces cas, on ne peut plus permuter les racines n'importe comment; elles sont deux à deux liées par paire.

Bref, Galois a constaté l'existence de permutations "admissibles" des solutions et a montré que le problème de la résolution était lié à la structure de l'ensemble de ces permutations. Il parle alors du "groupe de substitutions" associé à l'équation. Le terme "substitution" a par la suite fait place à "permutation" et actuellement, nous parlons du groupe de permutations.

Galois étudie ces groupes et en généralise l'étude à d'autres ensembles d'éléments. Il initie ainsi le développement de la théorie des groupes de permutations. Il faut noter que, dans la plupart des cas, les groupes de permutations considérés par Galois sont finis (ils opèrent sur un ensemble fini d'éléments).

Ces travaux, ainsi que plusieurs autres, dans le domaine de l'analyse, restèrent incompris pendant de longues années; ils ne furent publiés qu'en 1846 par Liouville, soit 14 ans après la mort de Galois.

Revenons aux groupes de permutations étudiés par Galois. Soit P un ensemble de permutations des éléments d'un ensemble E. Il est toujours possible de composer deux permutations p ₁ et p ₂ P mais, en général, on n'est pas assuré que la composée de p ₁ suivie de p ₂ , notée p ₂ p ₁ , appartienne encore à P. Mais ici, E est l'ensemble des solutions de l'équation et Galois étudie toutes leurs permutations "admissibles", c'est-à-dire toutes celles qui conservent les relations existantes. Dans ce cas, il est évident que:

Pour tout couple p 1 , p 2 P, p 2 p 1 P.

Lorsque l'ensemble E est fini, P est alors également un ensemble fini. Si P est un ensemble fini de permutations, pour toute permutation p P, il existe certainement une puissance naturelle (n) de p, telle que p ⁿ = I, la permutation identique. On appelle ordre de la permutation p, la valeur minimum de n. Dans ce cas, on a p ^n-1 p = I et p ^n-1 est la permutation réciproque de p. Dans ce cas, on dit qu'un ensemble fini de permutations P satisfaisant la condition ci-dessus, constitue un groupe de permutations.

Que se passe-t-il si P est infini ? Dans ce cas la démonstration n'est plus valable. Toutefois, dans les problèmes étudiés par Galois, la réciproque de toute permutation p "admissible" l'est également et appartient à l'ensemble P.

Pour tout p P, p -1 P

Cela conduit Galois à parler de groupes de permutations:

Un ensemble P de permutations est un groupe de permutations si et seulement s'il contient la composée de tout couple de permutations de P et la réciproque de toute permutation de P . Si P est fini, la seconde condition est automatiquement vérifiée.

Si, dans un groupe de permutations, on considère toutes celles qui conservent quelque "chose" (que ce soit un sous-ensemble, des propriétés, une structure donnée,...), elles formeront automatiquement un groupe de permutations.

Quoi de plus simple ! Cette simplicité est due au fait que dans un ensemble E, la composition de deux permutations, la permutation identique, la réciproque d'une permutation sont toutes des notions bien définies.

Remarque: L'associativité, dont on parle parfois, ne doit jamais être vérifiée quand il s'agit de permutations. En effet vérifier que p ₃ (p ₂ p ₁ ) = (p ₃ p ₂ ) p ₁ revient à vérifier qu'effectuer p ₁ suivi de p ₂ , suivi de p ₃ est la même chose qu'effectuer p ₁ , suivi de p ₂ suivi de p ₃ . Qu'y a-t-il de différent ? La position de la virgule quand on écrit, celle de la respiration lorsqu'on parle !

Revenons à l'histoire. Trente ans après Galois, le mathématicien britannique Cayley se pose une question intéressante. Lorsqu'on est en présence d'un groupe fini P de permutations, on peut écrire la "table de multiplication" ou plutôt de composition, des éléments de P. Comme un groupe de permutations contient nécessairement la permutation identique, Cayley l'écrit en tête des lignes et colonnes; il constate quelques propriétés évidentes mais remarquables. Si P possède n éléments dans chaque rangée (ligne ou colonne) de la table, tout élément de P s'y retrouve une et une seule fois. Toutefois, cette condition ne caractérise pas la table d'un ensemble de permutations. Cayley produit d'ailleurs un contre-exemple avec un ensemble de 5 éléments.

Quelle condition faut-il poser pour être assuré qu'une table puisse être considérée comme la table de composition d'un groupe de permutations ? Voici comment procède Cayley.

Il remarque que chaque rangée de la table de composition constitue une permutation des éléments de la rangée initiale. A partir de là, il fait correspondre à tout élément a la permutation p _a qui opère désormais sur les éléments de la table: si la loi de "multiplication" est notée *, la permutation p _a applique tout élément x sur a*x. Si la table est représentative d'un groupe de permutations, il faut évidemment que l'ensemble des permutations p _a forme un groupe de permutations et par conséquent la composée de deux quelconques doit appartenir à l'ensemble. Soit p _a et p _b deux permutations correspondant aux éléments a et b. En calculant la composée de ces deux permutations, on voit qu'un élément quelconque x est appliqué sur a*x par p _a ; ensuite p _b l'applique sur b*(a*x). Il faut que la composée des deux appartienne également à l'ensemble, autrement dit que p _b p _a soit une permutation p _c . Cela implique que pour tout x, il faut que b*(a*x) = c*x ; en particulier pour x = 1, on doit avoir b*a = c. La condition s'écrit donc : b*(a*x) = (b*a)*x et doit être valable pour tous a, b et x. En d'autres termes, la loi * doit être associative.

En résumé, Cayley obtient les conditions pour qu'un ensemble d'éléments muni d'une loi de composition corresponde à un groupe de permutations. Il lui suffit d'exprimer les premières constatations qu'il avait faites sur les tables de "multiplication" et d'ajouter la condition d'associativité.

Un ensemble muni d'une loi interne ; possédant un élément neutre et où tout élément possède un inverse , est un groupe si et seulement si la loi est associative .

Voici les conditions pour qu'un ensemble d'éléments muni d'une loi * soit un (ou possède une structure de) groupe. Remarque: On constate que la condition d'associativité correspond à la traduction de la première propriété rencontrée avec un groupe de permutations, à savoir: la composée appartient encore à l'ensemble.

On voit ainsi que les notions de groupe de permutations et de groupe sont à la fois différentes mais intimement liées. Tout groupe de permutations possède une structure de groupe (mais il ne faut évidemment pas en vérifier tous les axiomes!) et tout groupe (abstrait) peut être muni d'une structure de groupe de permutations.

Terminons comme nous avons commencé, par l'histoire.

Dans les Eléments d'Euclide, il est demandé que deux figures "égales" à une même troisième soient "égales" entre elles; actuellement, nous remplacerions "égale" par "isométrique". Que signifie cet axiome explicité par Euclide ?

En termes modernes, il demande qu'étant donné trois figures F ₁ , F ₂ , F ₃ s'il existe une isométrie T ₁ appliquant F ₁ sur F ₃ et une isométrie T ₂ appliquant F ₂ sur F ₃ , alors il existe une isométrie appliquant F ₁ sur F ₂ . Quelle est donc cette isométrie ? Il suffit d'effectuer T ₁ suivi de la réciproque de T ₂ . 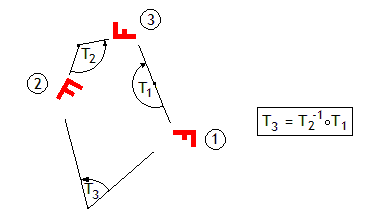Sur le schéma ci-contre, la figure F ₁ est appliquée sur F ₃ par la rotation T ₁ de 180°; la figure F ₂ est appliquée sur F ₃ par la rotation T ₂ de 120°. On voit que T ₃ obtenue en composant T ₁ avec T ₂ ^-1 applique F ₁ sur F ₂ . T ₃ est la composée d'une rotation de 180°suivie d'une rotation de -120°, donc une rotation de 60°.

En langage moderne, Euclide demande donc qu'étant donné deux isométries, le quotient (produit de l'une par l'inverse de l'autre) (T ₂ ) ^-1 T ₁ soit encore une isométrie. N'est-ce pas là tout simplement exprimer que l'ensemble des isométries est un groupe de permutations ? En effet, vérifier l'équivalence des deux définitions n'est qu'un simple exercice de logique:

si T₁ = T₂ alors le quotient vaut I (l'identité);
si T₁ = I, cela signifie de la réciproque de T₂ est également une isométrie;
enfin le produit de T₁ et T₂ n'est autre que le quotient de T₁ par (T₂)^-1.

Nous pouvons dire:

Un ensemble P de permutations est un groupe de permutations si et seulement si le quotient de deux quelconques appartient à P.

Un seul axiome suffisait à Euclide pour définir un groupe de permutations ! ...