Que vient faire cet article élémentaire dans un cours du secondaire? Sa présence est la réaction à un constat navrant.

Lorsqu'on demande à un élève ayant terminé ses études secondaires: ": "Pourquoi dit-on que (-2)*(-3) = +6 ?" la plupart du temps il répond "Parce que - par - égale +", ce qui prouve que cette "règle des signes" a, ou bien été présentée comme un dogme, ou bien été mal assimilée.

Approche algébrique (bien trop abstraite)

Les entiers sont définis par des couples de naturels (a, b) munis d'une relation d'équivalence (a, b)~(c, d) 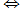a + d =b + c. Ce charabia deviendra plus compréhensible quand on aura expliqué que quand on écrit (a, b), on pense en réalité à l’expression a-b, (ce qui, pour l'instant, n'a de sens que si b est inférieur ou égal à a). On applique les mêmes règles que celles valables avec les naturels (principe de permanence). On définit le produit (a, b)*(c, d) = (ac +bd, ad + bc). Comme tout cela est intuitif !

Approche géométrique (ce n'est certes pas la plus simple)

Soit un rectangle dont les côtés sont donnés par les vecteurs a (parallèles à l'axe x), de coordonnées (a, 0) et b (parallèles à l'axe y) de coordonnées (0, b). Quelle est son aire? Pour cela, la valeur absolue de l'aire est évidente: c'est a* b, mais qu'en est-il de son signe? Arrangeons-nous pour que l'extrémité de a soit l'origine de b . Cela induit un sens de rotation autour du rectangle. Suivant que ce sens est horlogique ou contre-horlogique, nous dirons que l'aire est positive ou négative.

Approche intuitive (mais artificielle)

On étudie les gains et les pertes d'un commerçant. Voila une méthode parfaitement bien adaptée pour comprendre l'addition (la soustraction) des nombres positifs et négatifs. Par contre, la multiplication est plus difficile à aborder par cette voie. Bien sûr, on peut retirer une perte et cela procure un gain; on peut retirer trois fois la perte et cela est équivalent à un gain triple, mais tout cela est fort artificiel et confus.

Approche géométrico-algébrique élémentaire

On sait, depuis l'école primaire, que l'aire d'un rectangle de côtés A et B vaut AB. On modifie les côtés du rectangle en ajoutant a au côté A, et b au côté B. Que vaut l'aire du nouveau rectangle ? Evidemment, elle vaut (A + a)(B + b) ce qui peut s'écrire AB + aB + Ab + ab. Parfait ; mais si les corrections a et b sont négatives, les produits Ab et aB sont produits d'une nombre positif par un nombre négatif et il est vraisemblable que leur produit soit négatif. Il est un peu moins évident que le produit de a et b, tous deux négatifs soit positif. Et pourtant !

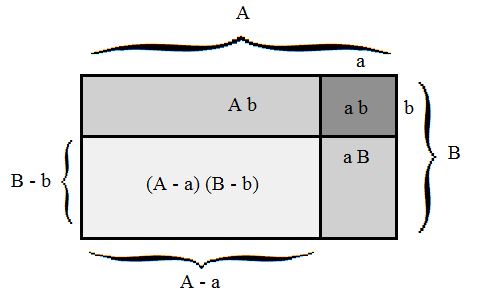
L'aire du nouveau rectangle s'obtiendra à partir de l'ancienne (A B) en retranchant tout d'abord un rectangle de côtés A et b, d'aire A b ; ensuite on retranche un rectangle de côtés a et B d'aire a B. Ce faisant on remarque qu'on a retranché deux fois le petit rectangle de côtés a et b d'aire a b! Pour réparer les dégâts, il faut évidemment en rajouter un. L'aire du rectangle de côtés A-a et B-b est donc AB - Ab - aB + ab.

Grâce à ces observations simples et intuitives, on comprend la fameuse "règle des signes".

Approche physique

Dans le cours de physique, on apprend que l'espace parcouru (lors d'un mouvement rectiligne uniforme) est le produit de la vitesse par le temps. Ces trois grandeurs possèdent un signe. L'espace, le temps, ainsi que la vitesse, peuvent tous trois être positifs, nuls ou négatifs. Voila quelque chose de concret qui semblera plus naturel aux élèves.

L'espace est mesuré à partir de la borne 0. Si l'on oriente la route de la gauche vers la droite (pour fixer les idées), un endroit situé à droite de la borne 0 aura une abscisse positive alors que, situé à gauche, son abscisse sera négative. Le temps est mesuré à partir de l'heure 0. Les événements postérieurs ont lieu à un instant positif, les événements antérieurs à un instant négatif. La vitesse est obtenue en mesurant la distance parcourue pendant l'unité de temps choisie; cette distance est positive ou négative suivant que le mobile se déplace de la gauche vers la droite ou en sens inverse. On peut également dire que la vitesse est le rapport entre l'espace parcouru et le temps mis pour le parcourir. Toutefois pour l'instant, nous laisserons cette définition de côté car elle pourrait faire appel à la "règle des signes".

Dès lors, il est très facile de faire des petits exercices avec les élèves. On donne, par exemple, la vitesse (avec son signe qui indique le sens du mouvement) ainsi que le temps (avec son signe également qui indique si on va dans le passé ou dans le futur) et on cherche la position du mobile. Il suffit de connaître la loi du mouvement rectiligne uniforme, ce qui est d'ailleurs connu dès l'école primaire. Au cours de physique, le professeur dira que l'espace parcouru est égal au produit de la vitesse par le temps et écrira e = v*t . Dans cette formule élémentaire, il ne faut jamais oublier que e, v, t ne sont pas des nombres, mais des grandeurs !

Soit dit en passant, il est curieux de voir la répugnance de certains professeurs de physique à utiliser des grandeurs plutôt que des nombres. Et pourtant que d'erreurs évitées dans les changements d'unités (p.ex. si on demande un résultat exprimé en km alors que la vitesse est exprimée en m/s et le temps en heures) et surtout vérification du résultat qui doit avoir la bonne dimension , c'est-à-dire celle d'une longueur!

Un quadruple exemple.

1. A l'instant t=0, je me trouve à la borne e=0. Si je roule à 80 km/h pendant 3 heures j'aurai parcouru 80 km/h*3 h. Au risque de nous entendre dire stupidement: " On ne divise pas des pommes par des poires ! " ou avec plus d'humour: " On ne multiplie pas des euros par des euros, sinon on obtiendrait des euros carrés, alors que tout le monde sait que les euros sont ronds ", n'oublions pas que km/h signifie 1 kilomètre divisé par 1 heure. En simplifiant par 1 h on obtient 240 km. Je serai donc à la borne 240 km
2. Que se passe-t-il si je roule dans l'autre sens, à la même vitesse et également pendant 3 heures ? J'aurai parcouru une distance égale à (-80 km/h)*3 h = -240 km (je me trouverai 240 km avant (ou à gauche de) la borne 0)
3. Si je roule à 80 km/h où étais-je 3 heures auparavant ? 80 km/h*(-3 h) = -240 km; avant la borne 0 évidemment.
4. Et finalement, si je roule vers la gauche où me trouvais-je il y a 3 heures ? (-80 km/h)*(-3 h) = 240 km (donc 240 km à droite de la borne 0)

Et voila pourquoi "- par - égale +"