Introduction

Les algorithmes de streaming apparaissent à de nombreux endroits et sont encore un champ actif de recherche par toutes leurs applications possibles et problématiques adjointes. Dans les exemples classiques, nous pouvons citer:

• Les routeurs qui peuvent détecter des communications malveillantes noyées au sein d’un flux ininterrompu de données ou essayer de stopper des transactions frauduleuses parmi celles légitimes (outlier detection/anomaly detection).
• Retourner les vidéos en top des "tendances" du moment.
• Systèmes de recommandations.
• Compressions de fichiers.
• Amélioration des performances pour des problèmes d’analyse des données de type OLAP.

Les problématiques que l’on rencontre avec les algorithmes de streaming sont assez transversales à l’informatique puisque plutôt appliqué et adapté aux problèmes de big data actuels. On peut retrouver de la réduction de dimensionalité, du machine-learning, du traitement des graphes, des problèmes en external memory model, ou des problèmes plus terre à terre comme de l’acquisition de données, de la compression d’images ou des modèles de calcul de type MapReduce.

Ce tutoriel est inspiré des cours donnés par M. Jelani Nelson de University of California, Berkeley, à l’époque professeur à Harvard, M. Raphael Clifford de University of Bristol et M. Alexandr Andoni de Columbia University.

Les sujets abordés dans cet article sont plutôt 'avancés’ et s’adresseraient donc de préférence à des étudiants en fin de master (licence pour nos amis français). C’est un domaine fort orienté statistiques, mais nous nous limiterons très fortement aux développements qui peuvent être faits. Néanmoins, il est préférable de connaître les 3 grandes inégalités que sont Markov, Chebyshev et Chernoff.

Nous allons commencer par évoquer des cadres théoriques pour discuter de ce genre de problématiques. Nous présenterons ensuite deux algorithmes fondateurs de ce champs d’étude, en mettant en évidence la manière dont on peut démontrer la justesse de l’algorithme ainsi que leur caractéristique statistique intrinsèque. Nous enchaînerons sur une vue assez haut niveau des principales avancées qui ont été opérées dans ce domaine et des idées brillantes qui ont pu émerger. Finalement, nous conclurons sur des notions qui ont été évincées et des pistes de réflexions pour aller plus loin.

• Cadre théorique
• Approximate Counting
• Count distinct elements
• Linear sketching & Count-Min sketch
• Sparse recovery
• Algorithmes sur les matrices

Cadre théorique

Jusqu’ici, nous n’avons pas encore défini ce que nous entendions par streaming algorithm ou "algorithme de fouille de flots de données" en bon français (selon wikipédia). Il s’agit d’un nom général donné aux algorithmes qui opèrent sur une flux continu de données afin de fournir une réponse. Cette famille se distingue des algorithmes qualifiés de online par trois caractéristiques principales:

• Consommation mémoire limitée.
• Temps de traitement minimal par unité de donnée.
• Réponse qui peut être délayée dans le temps.

En outre, les algorithmes streaming fournissent généralement une réponse approximative au résultat mais suffisamment proche du résultat attendu pour être exploitable et possèdent souvent des éléments non-déterministes.

Un élément central pour les algorithmes de streaming est la notion de sketch. Il s’agit d’une construction qui agit comme une nouvelle fonction, dénotée \(C(x)\), au regard d’une fonction que l’on souhaiterait calculer \(f\) et telle qu’elle permet de calculer ou d’approximer \(f(X)\) en n’ayant accès qu’au résultat de \(C(x)\). L’idée sous-jacente est que cette construction \(C\) agit comme une compression du problème. Ce concept est parfois étendu à deux dimensions avec \(f(X, Y)\) selon \(C(x)\) et \(C(Y)\) lorsque les algorithmes s’intéressent à des problèmes de similarité entre deux flux.

Un streaming algorithm consiste donc à maintenir le sketch \(C(x)\) à la volée, à chaque fois que \(X\) est mis à jour. L’idée sous-jacente étant de diminuer la dimensionalité du problème afin de pouvoir appliquer des algorithmes effectivement calculables sur la taille des données présentée. Attention que même si cette théorie rejoint des problèmes de compression, dimensionality reduction, etc … la finalité peut parfois être également différente comme dans l’usage de vouloir minimiser la quantité de données à acquérir en vue d’avoir une image suffisamment représentative et exploitable (ex: minimiser le temps dans un scanner IRM).

Cela sera mis en avant dans la construction de deux cadres théoriques différents, deux modèles de calcul, pour soutenir la construction des bornes supérieures et inférieures de complexité. On distingue généralement le Cash register model (modèle de la "caisse enregistreuse") et Turnstile Model (modèle "tourniquet")¹. Le modèle de la caisse enregistreuse se veut plus simple et ne permet que de compter les éléments du stream qui arrive. Il permet de répondre aux questions du type: "Combien d’éléments faut-il avoir vu, au minimum, avant de …". Le second modèle, du tourniquet, se concentre davantage sur les opérations du maintien du sketch à chaque élément, il se veut beaucoup plus puissant. Nous reviendrons principalement sur le deuxième modèle par la suite.

Approximate Counting

L’un des premiers problèmes connus des algorithmes de streaming est le: approximate counting par Robert H. Morris Sr. en 1978¹. Celui-ci consiste à fournir une estimation du nombre \(N\) d'événements en faisant un compromis entre le nombre de bits de stockage et la précision du résultat attendu. Il est clair que pour un comptage exact, il faudra au moins \(\log N\) bits (par le principe des tiroirs ou pigeonhole principle). Si on ne s’intéresse qu’à la puissance actuelle du nombre, on peut se contenter de \(\log \log N\). Mais quand est-il pour les autres cas ?

Dans le cas d’un comptage approximatif, on cherche un estimateur du nombre effectif d’événements \(\tilde{N}\) tel que les chances de trop se tromper soient suffisamment faibles, que l’erreur relative soit contenue:

$$\mathbb{P}(|\tilde{N} - N| \gt \epsilon N) \lt \delta$$

L'algorithme de Morris:

X <- 0 for each event: with probability 1 / 2^X: X <- X + 1 return 2^X - 1

L'idée consiste à ne compter qu'une partie des éléments en vue d'obtenir la meilleure approximation de l'exposant du nombre que l'on recherche, en se basant sur la propriété de Bernoulli qu'il faut en moyenne \(t\) événements pour qu'un élément avec une probabilité de \(\frac{1}{t}\) se produise.

Lorsqu'on tombe sur ce genre d'étrangetés, d'algorithmes peu communs, toute une série de questions émerge. Comment peut-on analyser ce genre d'algorithmes ? Pourquoi fonctionne-t-il ? Quelles sont ces caractéristiques statistiques ? Quelle est l'erreur maximale possible ? Que la probabilité que l'erreur relative soit supérieure à \(x\) ? Peut-on faire mieux, si oui dans quelle mesure, si non pourquoi ?

Nous allons commencer par démontrer pourquoi l'algorithme fonctionne et fournit un résultat "attendu". Pour cela, nous allons étudier son "invariant":

Posons \(X_{n}\) comme la valeur de \(X\) après \(n\) événements. On cherche à prouver que \(\mathbb{E}(2^{X_{n}}) = n + 1\). Par induction, nous savons que le cas de base (\(n=0\)) est correct. L'étape inductive consiste à démontrer que:

$$ \mathbb{E}(2^{X_{n + 1}}) = \sum_{i=0}^{\infty} \mathbb{P}(X_{n} = i) \mathbb{E} (2^{X_{n + 1}} | X_{n} = i) $$

La première partie du produit représente toutes les possibilités de l'état actuel du compteur après \(n\) événements, et la seconde la probabilité qu'on atteigne l'état suivant en fonction de l'état actuel. Or, nous savons que \(\mathbb{E} (2^{X_{n + 1}} | X_{n} = i)\) équivaut à: \(2^{i} (1 - \frac{1}{2^{i}})\) (la probabilité que le compteur ne soit pas modifié) + \(2^{i + 1} (\frac{1}{2^{i}})\) (la probabilité qu'il le soit). On peut voir cela comme un compteur binaire, où il faut que tous les bits précédents soient à \(1\) pour avoir le \(1\) qui suit.

On se retrouve avec:

$$ \mathbb{E}(2^{X_{n + 1}}) = \sum_{i=0}^{\infty} \mathbb{P}(X_{n} = i) 2^{i} + \sum_{i=0}^{\infty} \mathbb{P}(X_{n} = i)\\ \mathbb{E}(2^{X_{n + 1}}) = \mathbb{E}(2^{X_{n}}) + 1 = (n + 1) + 1 $$

L'invariant est démontré et laisse donc présumer que l'algorithme est correct dans l'objectif qu'il vise. Maintenant, que peut-on dire sur l'erreur attendue ? Pour cela, il suffit d'insérer le résultat précédent dans l'inégalité précédemment mentionnée:

$$ \mathbb{P}(|\tilde{N} - N| > \epsilon N) < \delta $$

On applique l’inégalité de Chebyshev² (ou de Markov):

$$ \mathbb{P}(|\tilde{N} - N| > \epsilon N) < \frac{1}{\epsilon^{2}N^{2}} \mathbb{E}(\tilde{N} - N)^{2} = \frac{1}{\epsilon^{2}N^{2}} \mathbb{E}(2^{X} - 1 - N)^{2} $$

On se retrouve avec une cochonnerie où on peut montrer³ que: $$ \mathbb{E}(2^{2X_{n}}) = \frac{3}{2}n^{2} + \frac{3}{2}n + 1 \, \text{et que} \, \mathbb{E}(\tilde{N} - N)^{2} = \frac{n^{2}}{2} - 2n - 1 \leq \frac{n^{2}}{2} $$

Et donc que:

$$ \mathbb{P}(|\tilde{N} - N| > \epsilon N) < \frac{1}{2 \epsilon^{2}} $$

Résultat plus que surprenant à première vue. Si je fixe ma probabilité d'erreur à \(0.1\), cela veut dire que \(\epsilon\) vaut \(\sim 2.2\) et donc qu'il y a moins de 10% de chance que l'erreur soit supérieure à une facteur \(\sim 2\) par rapport au nombre théorique. Si on ne s'intéresse qu'à l'échelle des grandeurs, ce résultat est assez exceptionnel.

Maintenant, si on veut améliorer l’approximation, on peut considérer \(K\) algorithmes de Morris⁴ et calculer leur moyenne, cela va réduire la variance (\(\frac{1}{2 K \epsilon^{2}}\)). Mais on peut aller encore plus loin ! En calculant la médiane des moyennes. En effet, la médiane nécessite que la moitié des estimateurs se trompent pour être erronée, mais si la probabilité de chacun de ces estimateurs est inférieure à \(\frac{1}{2}\), la combinaison de ces deux donnent une probabilité d’erreur qui décroît exponentiellement !⁵

Count distinct elements

Dans la section précédente, nous avons vu une manière d'approximer le nombre d'événements dans un flux. On peut aller une étape plus loin et demander le nombre d'événements distincts dans ce dernier.

Étant donné un stream de \(n\) éléments contenant \(t\) valeurs différentes (nombre a priori inconnu puisque c'est celui que l'on essaye de deviner), il existe deux algorithmes qui donnent un résultat exact. Le premier consiste à associer un bitset de taille \(t\) et à mettre à 1 le bit correspondant. Le second consiste à sauvegarder la liste des éléments vus en \(n \log t\). La complexité étant bornée par le minimum des deux, soit: \(O(min(t, n \log t))\).

Le premier algorithme pour résoudre ce problème a été énoncé par Philippe Flajolet & Nigel G. Martin vers 1983¹. Il se présente sous deux formes, une idéalisée et une réaliste.

Algorithme idéalisé:

Pick random hash function 'h': X <- 1 for each event: X <- min(X, h(x)) return 1/X - 1

Si vous êtes confus, c'est normal !

Premièrement, la fonction de hachage (aléatoire) prend en entrée n'importe quelle valeur possible (au moins tous les \(t\) éléments distincts) et retourne un nombre compris entre 0 et 1. Cet algorithme est idéalisé parce qu'il requiert de pouvoir stocker n'importe quel nombre réel ainsi que la fonction de hachage-même. Deuxièmement, on s'attend à ce que \(X\) valent, à peu près, \(\frac{1}{t + 1}\). En effet, si j'ai deux valeurs, la moyenne des deux vaudra soit 0, 1 ou '1/2'. Si j'en ai trois, je vais me retrouver avec 0, 1/3, 2/3 et 1. De manière générale, cela va séparer l'espace en \(t\) petites parties où on ne gardera que la valeur minimale.

Démonstration:

L'invariant est le suivant: \(X\) est une variable aléatoire qui est le minimum de \(t\) variables aléatoires, indépendantes et uniformément distribuées entre 0 et 1.

$$ \mathbb{E}(X) = \int_{0}^{\infty} \mathbb{P}(X > \lambda) d\lambda = \int_{0}^{\infty} \mathbb{P}(\forall i_{str} h(i) > \lambda) d\lambda = \int_{0}^{\infty} \prod_{r=1}^{t} \mathbb{P}(h(i_{r}) > \lambda) d\lambda $$

En effet, chaque résultat de la fonction de hachage est indépendant et la probabilité que \(h(i_{r}) > \lambda\) est \(1 - \lambda\) (puisqu'uniforme entre 0 et 1). Au final, on retombe sur l'invariant que l'on cherche:

$$ \int_{0}^{1} (1 - \lambda)^{t} d\lambda = \frac{1}{t + 1} $$

et il ne reste plus qu'à l'insérer dans notre inégalité en cherchant à calculer la variance, on a d'abord que:

$$ \mathbb{E}(X^{2}) = \int_{0}^{\infty} \mathbb{P}(X^{2} > \lambda) d\lambda = \int_{0}^{\infty} \mathbb{P}(X > \sqrt{\lambda}) d\lambda = \int_{0}^{1} (1 - \sqrt{\lambda})^{t} d\lambda = \frac{2}{(t + 1)(t+2)} $$

On calcule la variance:

$$ Var[X] = \mathbb{E}(X^{2}) - \mathbb{E}(X)^{2} = \frac{t}{(t+1)^2(t+2)} \lt \frac{1}{(t+1)^{2}} = \mathbb{E}(X)^{2} $$

Il ne reste plus qu'à réintroduire dans notre équation principale: \(\mathbb{P}(|\tilde{N} - N| > \epsilon N) < \delta\) grâce à Chebyshev:

$$ \mathbb{P}(|\frac{1}{t + 1} - N| > \frac{\epsilon}{t+1}) < \frac{(t+1)^{2}}{\epsilon^{2}} \frac{1}{(t+1)^{2}} = \frac{1}{\epsilon^{2}} $$

De manière générale, si la probabilité d'erreur apparaît avec un \(\epsilon\) au dénominateur supérieur à celui de l'erreur relative, cela veut dire que l'algorithme accomplit son devoir, et que c'est d'autant mieux que l'expression attachée est grande (la puissance 5 est meilleure que la mise au carré, par exemple).

Réalisme

Maintenant, il ne reste plus que le problème de la fonction de hachage. Afin de minimiser l'espace mémoire nécessaire pour encoder cette fonction, l'idée générale consiste à créer un ensemble de \(h\) fonctions hachages indépendantes entre-elles en se basant sur l'évaluation de polynôme dans un champ modulo \(p\) (\(\mathbb{F}_{p}[X]\)). Il est alors possible de stocker chacune d'entre elles en seulement \(O(h \log p)\) bits, tout en assurant le fait qu'elles soient deux-à-deux indépendantes³. On pourra ensuite combiner les différents estimateurs en vue de diminuer la variance attendue.

Quant aux réalisations dans \(\mathbb{R}\) entre 0 et 1, Flajolet & Martin¹ résolvent se problème en exprimant une sortie entre \([0;2^{L}-1]\) et en ne considérant que le bit de poids le plus faible (LSB). Ils proposent alors l'algorithme suivant.

BITMAP <- [0] * L for each event: i <- LSB(h(X)) BITMAP[i] <- 1 R <- index of left-most zero in BITMAP return 2 ** R / φ # 0.77351

La magie réside dans le fait que la probabilité d’avoir un nombre qui finit par la puissance \(2^{k}\) est de \(2^{-(k+1)}\) (partie du LSB). La constante magique désignée par \(\phi\) dans l’article original agit comme un facteur de correction pour améliorer la variance.

HyperLogLog

Comment ne pas aborder le célèbre algorithme du HyperLogLog de Flajolet, Fusy, Ganouet et al. en 2007² ? Il consiste en l’algorithme suivant:

m <- 2 ** b M <- [-inf] * m for each event: v <- h(X) j <- <v1 v2 v3 ... vb>2 # On prend les premiers b bits de v w <- <vb+1 vb+2 ...>2 # Les bits restants M[j] <- max(M[j], LSB(w)) Z <- 1 / sum(mj: 2 ** -mj, M) # L'indicatrice return alpha_m * m * m * Z

où alpha_m est donné par:

$$ \alpha_{m} = (m \int_{0}^{\infty}\log_{2}(\frac{2 + u}{1 + u})^{m} du)^{-1} $$

L'idée est la suivante, on va essayer de diviser équitablement le stream des \(n\) éléments vus en un ensemble de \(m\) sous-streams. Chaque sous-stream contiendra à peu près \(\frac{n}{m}\) éléments sur lesquels on va appliquer, indépendamment, l'algorithme de Flajolet & Martin. Le but étant de multiplier les estimateurs et de les combiner entre eux afin de réduire la variance dans le résultat.

Le maximum de chacun de ces sous-ensembles sera proche de \(\log_{2}\frac{n}{m}\). La moyenne harmonique (\(m * Z\)) des valeurs \(2^{\max}\) sera de l'ordre de \(\frac{n}{m}\) qu'il suffit encore de multiplier par \(m\) pour retomber sur l'ordre de \(n\). La moyenne harmonique a l'avantage d'*ignorer* les valeurs extrêmes. La variable \(\alpha_{m}\) sert de facteur de correction au biais multiplicatif de l'estimateur \(m^{2} Z\)..

Impact

Le problème précédent du count distinct elements et sa complexité sont très liés à une borne définie par Alon, Matias et Szegedy en 99³ où ils s’intéressent à la complexité minimale de l’estimation du \(k^{e}\) moment d’une distribution, qu’ils dénotent \(F_{k}\), et le cas de Flajolet & Martin représente '\(F_{0}\)'. C’est un problème assez profond en statistiques qui possède de nombreuses ramifications et implications. Voir Indyk 2006³, pour une vue des enjeux, problèmes ouverts et résultats connus (à l’époque) dans ce domaine. Pour le moment, Andoni, Krauthgamer et Onak fourniraient le meilleur algorithme au problème \(F_{k}\)⁴.

A première vue, ce genre de questions peut sembler assez étrange, mais il permet de répondre à des problèmes assez concrets comme le point query où on cherche à estimer le nombre de fois qu’un élément a été accédé ou le heavy hitter qui donne le sous-ensemble d’éléments qui ont été le plus accédé à X%⁵. Ce genre de requêtes est assez commun si vous pensez à des classements des tendances en temps réel, par exemple.

Linear sketching & Count-Min sketch

Linear sketching

Il existe deux modèles de calcul associés aux problèmes des streaming algorithms et qu’on qualifie de Cash register model (modèle de la "caisse enregistreuse") et Turnstile Model (modèle "tourniquet")¹. Grosso modo, le premier modèle ne s’intéresse qu’au nombre d’éléments nécessaires en entrée afin de calculer un résultat. Tandis que le second prend en considération une collection où les éléments du stream peuvent soit ajouter ou supprimer une valeur. Le second a des conséquences beaucoup plus profondes parce qu’il permet de démontrer des bornes de complexité et de designer des algorithmes par linear sketching.

Indyk et Woodruff ont publié une avancée majeure en 2005³ dans les problèmes de streaming qui a débloqué de nombreux problèmes avec la notion de linear sketching. Malheureusement, revenir sur ces problématiques nous écarterait trop du sujet initial et nous nous étendrons peu sur la question.

En très résumé, on peut représenter les résultats comme étant une matrice qui prend en entrée les éléments du flux \(X\) et fournit un résultat \(Y\) par produit matriciel. Évidemment, stocker la matrice \(M\) est trop lourd et on cherche la meilleure approximation. Quand on reçoit un nouvel élément \(\delta\), on veut calculer le nouvel \(Y_{i+1}\) comme \(M \times (X_{i} + \delta e_{i}) = M \times X_{i} + \delta M^{i} = Y_{i} + \delta M^{i}\). Toute l'intelligence réside dans le fait d'être capable de savoir calculer uniquement la \(i\) colonne de la matrice lors du traitement d'un nouvel élément et pouvoir mettre à jour la mémoire actuelle \(Y\).

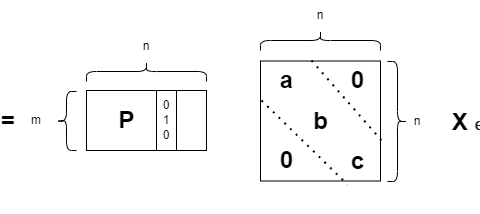
Count-Min Sketch

Une brique élémentaire, qui sert également de structure de données, de nombreux streaming algorithmes est le sketch du Count-Min introduit par Cormode & Muthukrishnan en 2005⁷ qui prolonge une idée de Charikar, Chen & Farach-colton dès 2002⁶. Il consiste en une matrice de taille \(L \times t\) où on associe \(L\) hash fonctions \(h_{r}: [n] \rightarrow [t]\) indépendantes par paire. Lorsqu’on reçoit un nouvel élément, on le hash par toutes les fonctions et on ajoute à la colonne indiquée la valeur associée. Chaque cellule de la matrice contiendra la somme des valeurs dont le hash aboutit à la même colonne. \(C_{a, b} = \sum_{i \in [n], h_{a}(i) = b} X_{i}\). Lorsqu’on fait une requête pour l’élément \(i\), on retourne le minimum de toutes les cellules ayant pour hash \(i\). Attention que cette hypothèse n’est vraie que dans le cadre d’un turnstile model qualifié de strict où on ne fait pas de suppressions, le meilleur estimateur étant de fait le minimum. Dans le cas de suppression, il faudrait prendre le médian.

Supposons pour un \(i\) fixe et un hash donné \(r\), et définissons l’indicatrice:

$$ Z_{j} = \begin{cases} 1 & h_{r}(j)=h_{r}(i)\\ 0 & \text{otherwise} \end{cases} $$

Par définition:

$$ C_{r, h_{r}(i)} = X_{i} + \sum_{j != i} X_{j} Z_{j} $$

En effet, le second terme correspond à l’erreur, à l’ensemble des autres termes qui sont rentrés en collision avec cette cellule. Mais, nous savons que:

$$ \mathbb{E}(\sum_{j != i} X_{j} Z_{j}) = \sum_{j != i} X_{j} \mathbb{E}(Z_{j}) = \sum_{j != i} \frac{X_{j}}{t} $$

L’astuce réside à choisir la taille de \(t\) et de \(L\) pour que tout fonctionne et si on pose que \(t = \frac{2}{\epsilon}\) et que \(L = \log_{2} \frac{1}{\delta}\), on a que:

$$ \sum_{j != i} \frac{X_{j}}{t} \leq \frac{\epsilon}{2} \left\| X \right\|_{1} \\ \mathbb{P}(\sum_{j != i} \frac{X_{j}}{t} > \epsilon \left\| X \right\|_{1}) \leq \frac{1}{2} \text{(Markov)} $$

et:

$$ \mathbb{P}(\min_{r} C_{r, h_{r}(i)} > X_{i} + \epsilon \left\| X \right\|_{1}) \leq \frac{1}{2^{L}} = \delta $$

Puisqu’il faut que tous les compteurs se trompent pour que le minimum soit erroné.

On arrive à ce que la complexité du sketch soit en \(O(\frac{1}{\epsilon} \log \frac{1}{\delta})\). Dans le papier original⁷, ils proposent une solution pour le heavy hitter en construisant un arbre de Count-Min où il suffit de faire un BFS afin d’obtenir tous les éléments recherchés.

Sparse recovery

Un autre problème des streaming algorithmes est celui du *sparse recovery*. Ce problème consiste à estimer la fréquence d'apparition d'un élément (\(f_{j}\)) associé à la clef (\(j\)), où l'on notera chaque élément du stream comme suit: \(\lt j, f_{j} \gt\). Pour cela, nous devons d'abord définir la notion de s-sparse stream, celui exprime qu'il existe au plus s éléments (qu'il faut comprendre comme "clef") avec une fréquence non nulle.

1-sparse stream

Pour le cas du 1-sparse stream, il suffit de calculer ces deux valeurs:

$$ l = \sum_{j=1}^{n} f_{j} \quad \text{et} \quad z = \sum_{j=1}^{n} j * f_{j} $$

Où \(n\) représente ici l'ensemble des clefs et il faut voir \(j\) comme la clef et \(f_{j}\) comme la valeur associée. À la fin, si \(l = 0\), on ne retourne rien. Sinon, on retourne \(\frac{z}{l}\).

Cet algorithme vous parlera peut-être plus dans un autre contexte, c'est celui qu'on emploie lorsque vous avez une permutation d'un array ayant pour valeurs \(0, 1, ..., n\) et que l'on cherche quel élément est absent dans celui-ci; il suffit d'appliquer la formule de Gauss et de soustraire par la somme.

Maintenant, si l'on souhaite retrouver la valeur associée, l'astuce consiste à calculer une preuve en travaillant dans l'arithmétique modulo p avec p tel que \(n^{3} \lt p \leq 2n^{3}\) (Bertrand–Chebyshev).

L’algorithme est le suivant:

l, z, p = 0, 0, 0 r <- random.rand(2, p) for each event (j, c): l <- l + c z <- z + c * j q <- q + c * (r ** j) if l == z == q == 0: return "error" elif z / l not in [n]: return "error" elif p != l * (r ** (z / l)) return "error" else: tmp <- [0] * l return tmp[z / l] = l

Sur un exemple concret, supposons que \(n = 2\) et \(p = 11\). Et posons que \(r = 5\). Pour le stream suivant: <2, 3>, <1, -2>, <2, -2>, <1, 2>.

• l vaudra successivement 3, 1, -1, 1
• z vaudra 6, 4, 0, 2
• q vaudra \((\text{modulo}\, p = 11)\) 3 * 5^2 = 75 (9), 75 + (−2) * 5^1 = 65 (10), 65 + (−2) * 5^2 = 15 (4), 15 + 2 * 5^1 = 25 (3).

Si on avait additionné chaque élément du stream par catégorie, on se retrouverait au final avec (0, 1), les "1" se sont bien annulés et il ne reste que "2" avec la fréquence 1. C'est algorithme fonctionne parce que si \(l = f_{i}, z = i*l\), on a que \(z/l = i \in [n]\). Et de fait \(q = f_{i} * r^{i} = l * r^{z / l}\). La probabilité d'erreur dépend du nombre de zéros sur lequel on peut tomber dans le polynôme associé à notre champ (la variable \(q\)) mais qui est en \(O(n^{3})\) ! Au final, au bout de \(n\) valeurs, on n'a que du \(O(\frac{1}{n^{2}})\).

s-sparse stream

Il ne reste plus qu'à généraliser ce procéder à \(s\). Et que fait-on quand on n'a pas d'idées ? On combine différentes solutions connues jusqu'à ce que ça marche ! Ici, l'astuce consiste à dispatcher les différentes entre \(2*s\) streams différents en prenant la position qu'il est fort probable que chaque stream se comporte comme un 1-sparse.

t <- log(s / delta) D <- [[0 for _ in range(2 * s)] for _ in range(t)] hashes <- [pick_independent_random_hash_from_n_to_2s() for _ in t] for each event (j, c): for hi, i in enumerate(hashes) update D[i, hi(j)] with (j, c)

On peut alors montrer que:

• L'espace mémoire nécessaire de en \(O(st (\log n + \log N))\) bits.
• Le temps d’exécution est en:
  • \(O(t) = O(\log s + \log \delta^{−1})\) pour chaque nouveau token.
  • \(O(tk) = O(s(\log s + \log \delta^{−1}))\) pour fournir les résultats.

Ce qui est plutôt pas mal du tout !

Streaming algorithms for Graph & Dynamic Programming

Ce n’est pas tout, on peut plonger encore plus profondément dans la folie et s’intéresser à des algorithmes sur des graphes dans des considérations de semi-streaming. Ce champ a été ouvert par Feigenbaum et al. en 2004¹.

Tout d'abord, on définit un algorithme en semi-streaming sur un graphe comme employant \(S(|V| = n, |E| = m)\) bits avec \(S(n, m)\) devant être de la forme \(O(n \text{poly} \log(n)) = O(n \log^{c}n)\), où l'algorithme peut revisiter toutes les arêtes (séquentiellement) en \(P(n, m)\) passes et utiliser \(T(n, m)\) temps par arête. Il a d'ailleurs été démontré que ce genre de complexité poly-logarithmique était minimal².

Par exemple, pour un spanning forest, afin de détecter la connectivité, on peut avoir l’algorithme suivant:

F <- set() for each edge as e: if not leads_to_cycle(F U e): # Vérifier que les deux sommets ne sont pas déjà dans F F <- F U e return 1 if is_tree(F) else 0 # F = n - 1

Mais quel est le rapport avec les s-sparse recovery ? La possibilité que l’on puisse reconstruire l’ensemble des arêtes incidentes pour chacun des nœuds du graphe ! Vous avez également de nombreux problèmes de type dynamic programming qui peuvent s’exprimer au travers de graphes et donc bénéficier de ce genres d’avancées³. De nombreux algorithmes ont pu être exprimés dans ce cadre de travail, parfois avec des solutions très élégantes: comme l’AGM sketch⁴ ou le maximal matching⁵.

Algorithmes sur les matrices

Une grande famille d’algorithmes et qui sont particulièrement intéressants dans le cadre du streaming sont les problèmes liés aux matrices. En effet, leur ubiquité dans les algorithmes de machine learning et de statistiques, de manière plus générale, les rendent indispensables dans ce cadre.

Approximate Matrix Multiplication

Véritable brique élémentaire, ce problème est évidemment à la racine de nombreux travaux. L’objectif est que l’on souhaiterait pouvoir multiplier deux matrices entre-elles, de manière efficace et sans trop d’erreur. De nombreux travaux se sont attelés à réduire la complexité du cas exact ou à essayer de trouver, a minima, des bornes inférieures de complexité théorique possible¹. Mais, dans le cas où on s’autorise des erreurs, peut-on réellement faire mieux ?

Il y a deux grands courants de pensée:

• La technique du sampling comme on peut la retrouver dans un papier en plusieurs parties de Drineas, Kannan & Mahoney en 2006². Cette technique, comme son nom l’indique, consiste à fournir une distribution de données suffisamment similaires à la source originelle et d’où la qualification de Monte-Carlo vu qu’on ne connaît pas à priori la distribution réelle sous-jacente. La méthode en elle-même consiste à construire deux nouvelles matrices qui synthétisent l'information originelle et ensuite de "bêtement" les multiplier entre-elles. Cet algorithme nécessite (au moins) 2 passes et possède une complexité en \(O(c(m + n + p))\) bits de stockage où \(c\) représente cette représentation intermédiaire (\(C\) estimé par \(A \in \mathbb{R}^{n \times m}\) et \(R\) par \(B \in \mathbb{R}^{m \times p}\)).

$$ \|AB - CR\|_{F} = O(\|A\|_{F} \|B\|_{F} / \sqrt{c}) $$

où \(\|.\|_{F}\) est la norme de Frobenius (la racine carrée de la somme des termes de la matrice au carré \(\sqrt{\sum a_{ij}^{2}}\)). Cette méthode a le défaut de dépendre des données, elle n'est pas oblivious aux paramètres, si la matrice est modifiée alors qu'on est en train de la traiter, la technique ne fonctionne pas.

• Et une par Sarlòs aussi en 2006³, dérivée d’un concept assez ancien en mathématique par W. B. Johnson et J. Lindenstrauss en 1984⁴ mais remis au goût du jour en 2006 par Ailon et Chazelle⁵ dans le but de trouver les voisins les plus proches (approximate nearest neighbour). L’algorithme emploie la notion de tug-of-war, hérité de l’estimation de moments⁶, qui consiste à prendre des bouts de matrices aléatoires puis à les combiner ensemble de manière intelligente en vue tout en ne conservant que des vecteurs assez clairsemé (sparse), on parle de projections aléatoires. Elle peut ne nécessiter qu’une seule passe, mais deux sont vraiment nécessaires et requiert \(O((m + n + p) * (\epsilon^{-2} \log \frac{1}{d} + (\log \frac{1}{d})^{2})\) bits d’espace mémoire et est oblivious.

Chacune de ces techniques a mené à de nouvelles explorations qui continuent encore aujourd’hui⁷ et très liées aux questions du subspace enconding et de la réduction de dimensionalité.

Ensuite, il y a eu un papier assez influent de Clarkson et Woodruff sur les extensions possibles aux algorithmes d’apprentissage automatiques (comme les SVM, perceptrons)⁸. En réemployant les approches itératives plutôt que les solutions exactes comme pour les moindres carrés, par exemple.

Les notions peuvent également servir aux problèmes de recommandation où, in fine, on cherche, sur base de quelques appréciations de la part d’un utilisateur, à retrouver toutes les notes qu’il pourrait attribuer. Reconstruire sa "ligne" dans la matrice en ne possédant que quelques éléments. L’une des suppositions est très souvent l’aspect low-rank de la matrice (qu’elle est essentiellement vide), en effet, rares sont les utilisateurs à avoir vu tous les films du catalogue.

Conclusions

Dans cet article, nous n’avons fait qu’effleurer qu’une infime partie des problèmes qui peuvent apparaître dans le cas des streaming algorithmes. Nous n’avons pas vraiment mis en avant la différence qui peut exister entre les algorithmes déterministes (deterministic), déterministes approximatifs, aléatoires (randomized) ou aléatoires approximatifs avec leurs deux interprétations ("Monte-Carlo" peut se tromper et "Las Vegas" ne se trompe pas, mais dont le temps d’exécution n’est pas défini).

Toutes les notions de complexité et de bornes inférieures (lower bound) ont également été évincées, malgré un modèle de calcul associé la communication complexity. Ou encore les problèmes de réduction de dimensionnalité et les travaux de Andoni sur le local sensitive hashing¹. De même que leurs applications directes dans le compressed sensing, l’acquisition de données, leur traitement et compression.

Si ce genre de sujets vous a intéressé et, en particulier, la partie plus statistiques, Philippe Flajolet & Robert Sedgewick sont deux très renommés chercheurs à l’origine du champ que l’on appelle: Analytic Combinatorics² et à l’origine de bon nombre de démonstrations en complexité. Attention, il s’agit vraiment d’un domaine 'avancé' en informatique et qui nécessite de solides bases en mathématiques.