Introduction

Dans cet article, nous allons revenir sur le concept fondamental que représente la notion de "modèle de calcul" dans le cadre de l’informatique. Ces modèles agissent comme des abstractions mentales à l’élaboration d’une solution à un problème en fournissant un cadre de travail simple et élégant. Ils servent à décrire comment il est possible de calculer efficacement une fonction, voire si cela est même possible; ceux-ci sont à la base des notions de calculabilité et de complexité.

Nous commencerons par présenter une tentative de définition, nous verrons ensuite l’historique des premiers modèles, les raisons qui ont poussé à la création de ce concept, leurs évolutions et les différentes notions qui leur ont été adjointes afin d’aboutir sur le modèle de calcul le plus usité actuellement. Nous reviendrons ensuite sur différents modèles présentant des avancées majeures, que ce soit par leurs nouveaux concepts apportés ou leur domaine d’application.

Cet article ne demande pas de compétences informatiques "techniques" en soi, mais nécessite une certaine compréhension du domaine et s’adresserait donc davantage à des personnes ayant déjà quelques notions de complexité, sans doute l’équivalent de 2e année de bachelier (licence pour nos amis français).

Définitions

Mais dans le fond, qu’est-ce qu’un modèle de calcul ? Cela fait partie de mots qui sont employés parce que les gens en ont une compréhension intuitive, mais qu’il est très difficile de formaliser parce qu’associer à des sujets qui peuvent être très différents. Cela fait partie des termes qu’on décrit plutôt par des exemples que de manière formelle.

Tout d’abord, lorsqu’on parle de modèle de calcul dans le cadre de l’informatique, on parle de model of computation. Mais, il existe un autre concept, plus "général" et que l’on nomme computational model(-ing), qui s’intéresse à l’abstraction des systèmes¹. Dans le cadre qui nous intéresse, model of computation, on cherche à proposer un cadre de travail qui permet de facilement capturer la complexité que l’on essaye de représenter. La notion de simplification et de représentation d’un système ou abstraction est assez cruciale. En tant qu’humain, nous aspirons à rationaliser notre pensée par des biais plus ou moins formels, mais il y a un profond fossé entre des notions de logique mathématique et la manière dont on conçoit des solutions informatiques.

Les modèles de calcul visent à définir un ensemble de règles, qui se veulent les plus simples possibles (des véritables briques élémentaires), mais qui permettent de soutenir la représentation mentale que l’on se fait d’un problème. Le but étant alors de combiner toutes ces petites briques afin de construire la solution la plus adaptée à notre problème. Chacune de ces opérations vise à effectuer une action simple (comme additionner deux nombres, en stocker un en mémoire), et souvent associée à une action concrète dans le monde réel, qui pourra être combinée avec d’autres afin de réaliser des programmes toujours plus complexes. Ces modèles ne décrivent pas un processus informatique, mais décrivent ce quelque chose informatiquement².

Nous savons quelle procédure appliquer pour résoudre des équations du second degré en suivant les opérations de base de l’arithmétique (qui correspond, ici, à notre modèle de calcul). De même, nous sommes capable de suivre une recette de cuisine et préparer une ratatouille en ne sachant que découper des légumes et les faire cuire (modèle de calcul).

Deux observations émergent de cette définition:

• Premièrement, on est capable maintenant de définir des notions de complexité puisqu’il suffit de compter le nombre de briques employées ainsi que leur type. Réciproquement, si l’on change le modèle de calcul, la complexité va évoluer en conséquence.
• Deuxièmement, la notion de calculabilité (calculability) émerge, la question de fond étant: "Est-ce qu’avec ces briques, je suis capable de résoudre mon problème ?" ou plus largement: "Quels sont tous les problèmes pouvant être résolus avec ces briques ?"

Historique

On considère généralement que le premier modèle de calcul date de la Grèce Antique, aux alentours de -300 avec Euclide. En effet, il est l’un des premiers à avoir apporté la notion d’axiomes (briques élémentaires) qui serviront de base à la démonstration de théorème en géométrie. Ces axiomes décrivent un ensemble d’opérations tel que, par exemple, il est toujours possible de construire une droite passant par deux points, ou que, étant donné un segment de droite, il est possible de dessiner un cercle dont la taille du rayon est la même que celle du segment. Ce modèle de calcul est qualifié de la règle (non graduée) et du compas.

Outre résoudre le problème des nombres irrationnels qu’avait soulevé l’école des pythagoriciens, ce modèle a permis d’offrir un cadre de travail simple et élégant à des fins de démonstrations, mais également d’engager la communauté mathématique dans la recherche de résolutions impossibles, comme la quadrature du cercle, la trisection de l’angle ou la duplication du cube. En effet, la notion de calculabilité n’était même pas conçue à l’époque et, il était naturel de penser que l’on pouvait tout démontrer. Seulement, l’histoire montrera que la trisection de l’angle et la duplication du cube nécessitèrent la résolution d’équation du 3e degré (alors que la règle et le compas ne savent résoudre que le 2e degré) et la quadrature du cercle requiert le concept de transcendance (et donc quitter le monde algébrique !). Mais qu’en est-il de la calculabilité en cas d’une règle graduée ou de l’origami¹ ?

Ces problèmes antiques ne connurent qu’une conclusion très tardive. En effet, il a fallu attendre les travaux de Gauss–Wantzel pour le concept de nombres algébriques ou de von Lindemann en 1882 pour la transcendance de \(\pi\) ! On peut s’étonner d’une résolution si tardive, plus de 2000 ans se sont écoulés entre l’énoncé et la résolution des problèmes. Il faut comprendre qu’un profond mouvement de standardisation et de rigueur a commencé à émerger dès la fin du XVIIIe, prémices qui seront connues sous le nom de crise des fondements. La langue de l’algèbre s’est développée et son usage est devenu plus global grâce à l’augmentation du nombre de mathématiciens et de la "mondialisation", ce qui a permis un transfert des connaissances plus efficaces. Par l’algèbre, les mathématiques se sont voulues davantage rigoureuses, corroborées par les nouveaux concepts d’algèbres et le pouvoir de démonstration de ces briques plus fondamentales (travaux de Abel et Galois). L’autre aspect majeur du XIXe est la multiplication de paradoxes. L’analyse sera complètement redéfinie par Cauchy et Weierstrass, les autres domaines mathématiques seront également chamboulées et connaîtront des modifications profondes.

C’est également à la fin du XIXe siècle que l’on verra apparaître la logique mathématique qui visait à résoudre cette crise des fondements, par le biais de travaux de De Morgan, Boole, Frege, Peano, Russell ou Hilbert. Cela a abouti à fournir une fondation axiomatique aux mathématiques au travers de systèmes logiques formalisés. Le plus célèbre étant sans doute la construction des nombres naturels au travers de l’axiomatique de Dedekind–Peano² qui conduisit à des résultats divers qui menèrent Hilbert à se poser les questions suivantes: "Peut-on prouver qu’il n’existe pas de contradictions parmi tous les théorèmes exprimables dans une base axiomatique ?", "Est-il possible de prouver automatiquement des théorèmes grâce à un algorithme ?" ou "Est-il possible de toujours construire un algorithme qui répond par oui ou non à une question ?" (Entscheidungsproblem)³

Finalement, vers 1930, émergèrent les premiers formes de fonctions calculables (computable function). Ces constructions mathématiques ont permis de faire le lien entre un cadre théorique et la notion intuitive de calculabilité, c’est-à-dire la description d’une procédure finie (un algorithme) qui permet de calculer la fonction. Il y a eu trois grands modèles de calcul développés quasi-successivement: les fonctions récursives (general recursive functions) de Gödel-Herbrand en 1933⁴, le \(\lambda\)-calcul de Church en 1936⁵ et la Turing machine de Turing vers 1936⁶. Toutes ces découvertes furent sublimées dans la thèse dite de "Church-Turing" qui résolut plusieurs théorèmes importants, et ce, dans un contexte très facilement compréhensible à des personnes non-initiées. Le parachèvement est sans doute la notion de la machine universelle de Turing, qui établit l’équivalence de ces différents modèles de calcul en démontrant qu’il est possible de lire et de reproduire le comportement de n’importe quelle procédure d’un autre modèle.

RAM-machine

Ce nouveau contexte mathématique ainsi que l’arrivée de la deuxième guerre mondiale a permis de redonner un coup de neuf à la notion de calculateurs analogiques (analog computer). Il était maintenant possible de résoudre des problèmes de manière systématique grâce à un ensemble de pièces mécaniques standardisées ("axiomes") et d’éventuellement reprogrammer la machine afin d’effectuer une autre tâche ! Ces machines analogiques étaient des merveilles de technologies et permettaient de résoudre des problèmes très complexes comme calculer (numériquement) des intégrales ou piloter des tourelles d’artillerie. Grâce à l’invention du transistor, il fut enfin possible de réduire la taille de ces machines et d’améliorer leurs performances.

D’un autre côté, outre les avancées technologiques prodigieuses qui se produisirent au XXe siècle, les scientifiques continuèrent de développer ce champ que l’on nommera informatique, que ce soit par l’émergence du concept de langage formel qui aboutira à la création des premiers langages de programmation, ou la conception du fonctionnement de ces ordinateurs et de leur réalisation.

Les premiers travaux consistèrent à examiner les capacités de cette machine de Turing, que ce soit en terme de calculabilité, ou afin de déterminer s’il était possible de réduire le nombre d’axiomes ou de les exprimer d’une autre manière (plus élégante). L’idée étant évidemment de faire coïncider le modèle mental des langages de programmation aux capacités de la machine, on pensera notamment au modèle de Post¹ ou de Wang² ainsi qu’aux premiers compilateurs dans les années 50.

On dénomme par "machine à registres" (register machine) les modèles de calcul qui se veulent plus proche des capacités matérielles (et donc plus "faciles" à implémenter physiquement), tout en étant équivalent à la machine de Turing et conceptuellement plus simples. Les premières machines sont dites à "compteurs" ou counter machine et consistent simplement en un endroit où est stocké un programme, une mémoire qui enregistre la position actuelle du programme et de différents compteurs qui permettent de faire des calculs. Ensuite, fut ajoutée la notion d’accès indirect à la mémoire (au travers de mémoires intermédiaires, ce qu’on appelle communément les pointeurs), cette capacité était cruciale par les possibilités qu’elle offre en pratique. David Wheeler prononça l’aphorisme suivant: "All problems in computer science can be solved by another level of indirection"³.

Avec l’apparition des premiers langages de programmation "haut niveau", l’étude de la complexité devint plus aisée et assez centrale. Analyse qui fut simplifiée par une correspondance assez directe entre les capacités des langages de l’époque et le nombre d’instructions réellement exécutées par la machine. Et la machine à accès aléatoires (random acess memory machine ou RAM-machine) fut un de facto standard de par sa simplicité, sa facilité analytique et son équivalence directe avec les capacités matérielles. Il faut l’imaginer comme étant un jeu d’instructions simples, proche d’un assembleur assez réduit avec l’abstraction qu’accéder à des registres ou à de la mémoire est essentiellement la même chose.

Actuellement, on emploie un modèle de calcul plus proche du C par ses capacités. On permet nettement plus d’opérations possibles, mais également des plus complexes telles que: calculer \(sin(x)\) ou accéder à l’arête suivante dans un graphe. On met beaucoup plus en évidence l’abstraction que l’on considère en fonction de l’analyse que l’on effectue. On peut étudier plus précisément la complexité de la fonction \(sin(x)\) ou bien la considérer comme "acquise" et comme ayant le même coût qu’additionner deux nombres par exemple. La différence fondamentale étant vraiment la pondération que l’on attribue au modèle et à ses capacités.

D'autres modèles

Circuit

Pourtant, on comprend bien qu’il est bien plus difficile d’effectuer la division entre deux nombres que leur addition. La taille incombe également, additionner deux très grands nombres sera sans doute plus lent que deux petits. Il faut alors être capable d’exprimer ces opérations déjà élémentaires en des atomes encore plus petits. On cherche alors à quantifier la taille du nombre dans sa représentation et la quantité de matériel nécessaire pour réaliser cette dite opération. On observera alors que tous les nombres partageant le même bit de poids fort consommeront de fait, les mêmes besoins de travail. Et qu’un changement de base à des impacts très profonds sur la complexité. Le test de primalité est d’ailleurs linéaire dans une base unaire.

L’un des premiers modèles de calcul développé fut d’ailleurs le modèle circuit¹. L’idée est de représenter un calcul comme un graphe dirigé et acyclique dans lequel chaque nœud ou porte (gate) correspond soit à une entrée, soit une opération binaire élémentaire (AND, OR, NOT) ou encore une sortie. La taille du circuit étant définie par le nombre de portes nécessaire et la profondeur comme le chemin de taille maximale entre l’entrée et la sortie. On remarquera que ces deux notions cherchent à optimiser deux critères différents. En effet, le prix sera influencé par le nombre de portes, mais la rapidité par la profondeur, il faut donc essayer d’optimiser selon ces deux aspects simultanément. Par ailleurs, cette théorie mena à des classes de complexité propres puisque évoluant dans un tout autre modèle mental (qualifiée de AC²).

Mathématiques

Dans les modèles plus "mathématiques", deux se sont fait particulièrement remarquer tant par la théorie qui leur est liée que la démonstration de complexités encore inconnues. Ils ont été également dans les premiers résultats sur la notion de complexité minimale possible pour un problème, le fameux \(\Omega(.)\).

Arbre de décision

Le premier agit comme un arbre de décision (decision tree model) qui sera étendue à celle d’arbre de décision algébrique (algebraic decision tree³). Grosso-modo, le modèle n’est capable que d’une seule chose, de comparer des résultats entre eux (en étudiant le signe de la somme de différentes entrées par exemple). Le résultat le plus connu est la démonstration de la complexité en \(\Omega(N \log N)\) du tri⁴. L’idée est que l’on souhaite trier une collection de \(N\) éléments, ceux-ci peuvent être dans n’importe quelle position, il y a donc \(N!\) combinaisons possibles. Maintenant, à chaque fois que l’on va comparer deux éléments, on va devoir effectuer un choix afin de déterminer quelle comparaison effectuer ensuite. Ce nombre de choix augmente de manière exponentielle.

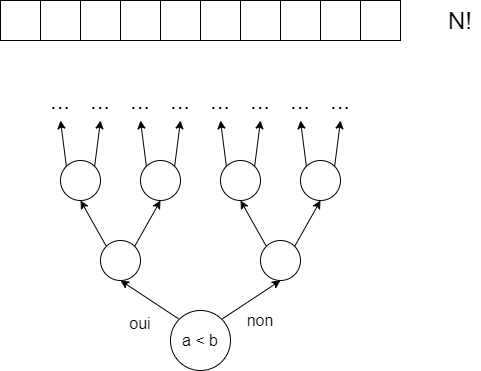
On se demande donc, combien faudrait-il effectuer de choix, au minimum, afin d’être capable de générer toutes les combinaisons possibles ?

$$ 2^{k} \geq N! = k \geq \log_{2}(N!) = k \geq \Omega(N \log N) $$

Théorie de l’information

L’idée sous-jacente à la théorie de l’information est qu’un algorithme essaye de découvrir la vérité. Cet algorithme joue face à un oracle qui donne une réponse à chaque question que l’algorithme pose. Sa réponse ne changera pas, mais il peut toujours donner la pire réponse correcte possible (sous-entendu le pire cas - \(O(.)\). Si nous reprenons le problème du tri, l’oracle fournit une permutation aléatoire (et uniforme) des données et ne répond que par oui ou non aux questions que l’algorithme lui pose. L’algorithme va pouvoir alors exercer un ensemble de requêtes, dépendantes de la permutation, afin de d’arriver à la conclusion que les données sont bel et bien triées. On compte alors le nombre d’appels nécessaires effectués à l’oracle.

Autres modèles mathématiques

De grandes familles de modèles de calcul sont directement issues des concepts des langages formels. En effet, à chaque langage est associé une machine abstraite (ainsi qu’une grammaire) qui possède ses propres capacités (calculabilité) et éventuellement complexités spécifiques. Une double question peut émerger de ce fait: Quelle est la machine la moins puissante qui permet de répondre à un problème ? Quelle est la fonctionnalité minimale à fournir au modèle afin de réduire la classe de complexité ?

Une bonne partie de ces modèles de calcul ont été envisagés sous un aspect plus probabiliste et statistique. L’idée étant de pouvoir caractériser des notions comme les concepts de performances "moyennes" d’un algorithme, par exemple. Ou les algorithmes qualifiés de probabilistes et fournissant une réponse à X% de réussite après un certain nombre d’étapes ou bien, tout simplement, ceux incorporant directement des décisions aléatoires dans leur processus (non-déterminisme).

Cache & espace

La RAM-machine est généralement employée afin de calculer une complexité temporelle puisqu’il suffit de dénombrer le nombre total d’instructions effectuées par le programme et de le multiplier par le temps moyen d’une instruction. Bien sûr, on peut raffiner ce modèle en donnant des poids plus ou moins forts à certaines opérations. Mais, on peut surtout mesurer deux autres aspects grâce à la description de cette machine. Par exemple, on peut s’intéresser à la complexité spatiale, à la quantité d’espace mémoire nécessaire afin de résoudre le problème et donc à l’efficacité dont on fait preuve par rapport à la réutilisation de l’information⁶.

Un autre aspect est lié aux avancées technologiques de nos processeurs, l’essentiel du temps est désormais passé dans l’attente des données en vue d’être calculé. On peut alors étudier la complexité d’un algorithme sur la quantité de données échangées entre une mémoire lente et celle immédiate des processeurs; on parle de modèle IO ou external memory. Il y a des relations très profondes qui unissent les complexités temporelles, spatiales et IO et il s’agit d’un domaine d’études encore fort actif⁷.

Multicore

Maintenant, pratiquement tout ce qui nous utilisons est composé de plusieurs machines, que ce soit par l’utilisation de serveurs ou de threads. Il y a deux grands paradigmes qui s’opposent:

• Ceux qui prennent la position d’étendre simplement le modèle RAM aux fonctionnalités parallèles, on parle de PRAM, généralement plus adapté à la représentation de nos processeurs ou cartes graphiques. Il y a différentes variations sur les capacités des machines en elles-mêmes. On fait généralement la distinction entre trois concepts: le step (la quantité de travail séquentiel, comme le fait de devoir lancer les threads), le work (la quantité de travail effectué par chaque thread) et le total work (la quantité totale de travail effectué par tous les threads). On peut également se poser les questions suivantes: Ont-elles le droit d’écrire au même endroit ? Partagent-elles toute la même mémoire ? Comment peuvent-elles communiquer et à quel coût ?⁸
• Ceux qui prennent le contre-pied total et étudient davantage la communication et la synchronisation entre les unités parallèles. Classiquement, on présente le modèle BSP⁹ qui consiste à effectuer une série de calculs indépendants, d’attendre qu’ils aient tous terminés, partager les données et recommencer. On compte alors le nombre de partage et/ou le délai d’attente entre deux phases. L’extension grand-public la plus connue est le modèle map-reduce¹⁰ qui consiste en deux étapes, les calculs et la transmission et échange des données.

Conclusions

Dans cet article, nous avons très brièvement survolé les grandes familles de modèles de calcul qui existent. Il va s’en dire qu’il ne s’agit que d’une infime partie parmi les idées brillantes qui ont pu émerger ces 80 dernières années ! Tout au moins, nous espérons avoir présenté les grands axes de ce domaine, les familles et logiques liées aux avancées technologiques ou raffinements sur des questionnements scientifiques plus précis.

Nous espérons que, à la lecture de cet article, vous vous posiez des questions plus profondes sur la manière dont on définit la complexité des algorithmes. Quelles hypothèses sont effectuées par rapport à sa complexité ? Nous avons vu quelques modèles qui s’intéressent à d’autres problématiques tels que le nombre de cache lines lues ou la taille de la mémoire consommée. Peut-être faut-il alors chercher un algorithme qui est le "meilleur" par rapport à plusieurs modèles de calculs ? Peut-on trouver un algorithme idéal, optimal, sans la moindre hypothèse sur le modèle en lui-même, concept appelé obliviousness. Il faut néanmoins bien garder à l’esprit que ce sont avant tout des abstractions effectuées et qu’il faudra toujours mesurer en pratique, d’autant plus que les avancées technologies tendent à rendre les résultats très dépendant du matériel employé.

Je n’ai pas connaissance de livres spécifiquement dédiés aux modèles de calcul et à la comparaison de ceux-ci. En effet, le problème étant que chaque type de modèles possède généralement une littérature très fournie qui n’a pas forcément été circonstanciée au travers d’un livre, certains domaines étant trop récents que pour les considérer comme "clos".

Si ces questions à l’origine de l’informatique vous intéresse, il existe le fameux livre, quelque peu curieux, de D. Hofstadter: "Gödel, Escher, Bach"¹ avec une vision très transversale des notions de récursivité ou de calculabilité.