Il s'agit d'un petit jeu mathématique fort ancien (rien à voir avec le sudoku qui fait fureur pour l'instant) On prend un quadrillage de \(n×n\) carrés dans lesquels il faut placer les \(n^2\) premiers nombres naturels à partir de \(1\), afin que la somme des nombres de chaque rangée (ligne ou colonne) soit la même et vaille \(k\). Remarquons déjà que la condition de partir de \(1\) n'a rien d'essentiel; il suffirait d'ajouter une même constante à chaque élément du carré. On pourrait également demander de ne considérer qu'une suite d'entiers en progression arithmétique. Comme ce problème n'est pas très difficile, on peut le raffiner en lui imposant des conditions supplémentaires. On peut exiger en outre que la somme des éléments de leurs deux diagonales vaille également \(k\), et on les appellera "magiques". Ce nombre \(k\) sera appelé la constante du carré.
Un exemple est donné par un carré 6×6 (datant du XIIIe siècle) dont chaque rangée ainsi que chaque diagonale a pour somme 111.
 |
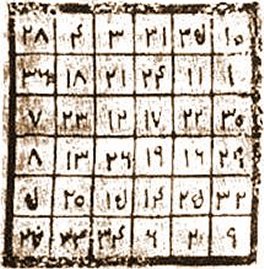ce qui équivaut, dans nos notations, à : |
|
Un autre exemple: on trouve dans la gravure " Melancholia
" (1514) de Dürer un carré magique 4×4. Quelle que soit la rangée (ligne ou colonne), la somme des éléments vaut toujours 34. De plus, les nombres sur les diagonales et dans chacun des 4 petits carrés 2×2 situés aux quatre coins du grand, ainsi que celui situé au centre, ont toujours la même somme: 34.
Soyons plus modestes et intéressons-nous aux carrés \(3×3\).
L'exemple le plus connu consiste à n'utiliser que les \(9\) premiers nombres naturels, et un résultat est par exemple:
| \(8\) | \(1\) | \(6\) |
| \(3\) | \(5\) | \(7\) |
| \(4\) | \(9\) | \(2\) |
Mais élargissons le problème en levant la condition que les nombres figurant dans ce tableau \(3×3\) soient des naturels, et supposons qu'ils puissent être rationnels ou même réels.
Si l'on convient de dire que \(m\) fois un carré est simplement le carré magique dont tous les éléments ont été multipliés par \(m\), le carré obtenu est évidemment encore magique ! Comme \(m\) peut être un rationnel ou un réel, voila bien une raison nécessaire de se libérer des naturels. De plus, le carré somme de carrés magiques (c'est-à-dire le carré obtenu en sommant les éléments correspondants de chaque case) est également magique.
Désignons les neuf éléments du carré magique, de constante \(k\), par les 9 premières lettres de l'alphabet.
| \(a\) | \(b\) | \(c\) |
| \(d\) | \(e\) | \(f\) |
| \(g\) | \(h\) | \(i\) |
On peut écrire 8 relations entre ces 9 éléments inconnus: la somme est constante dans chaque ligne (3 équations), chaque colonne (3 équations), et sur chaque diagonale (2 équations). Pour quelqu'un habitué aux mathématiques (mais qui ne réfléchirait pas trop), il serait tentant de dire qu'il ne reste qu'une seule inconnue, puisqu'il existe 8 équations entre les 9 éléments inconnus.
Grave erreur, car les relations ne sont pas indépendantes !
En effet, la somme de tous les éléments du carré est égale à \(3k\). Mais on peut regrouper les termes de cette somme et voir cette équation comme la somme des termes de chacune des lignes, mais aussi la somme des termes de chacune des colonnes. Il nous reste donc bien plus qu'un seul paramètre.
En écrivant la somme des éléments situés sur les 2 rangées et des 2 diagonales contenant le nombre \(e\) situé au centre du carré, c'est à dire les sommes \(d+e+f\), \(b+e+h\), \(a+e+i\) et \(c+e+g\), toutes égales à \(k\), on obtient \(4k\). Dans cette somme, chaque élément une seule fois à l'exception de l'élément central \(e\) qui apparaît 4 fois. On en déduit que la somme de tous les autres éléments vaut donc \(4k-3e=3k\). On obtient donc \(k=3e\)
Munis de cette information, essayons de construire un carré dont la constante vaut \(k\). L'élément \(e\) est bien déterminé : \(e = k/3\). Il est évident que si on soustrait \(k/3\) de chacun des éléments, le carré reste magique et que sa constante vaut \(0\).
Nous sommes ramenés à un problème plus simple. La somme des éléments de chaque rangée et de chaque diagonale doit être nulle. Il en résulte que deux éléments symétriques par rapport au centre sont opposés. Ce carré doit être de la forme:
| \(p\) | \(q\) | \(r\) |
| \(s\) | \(0\) | \(-s\) |
| \(-r\) | \(-q\) | \(-p\) |
Mais il faut également que \(p+q+r=0\) et de même \(p+s-r=0\).
Les deux autres rangées n'apportent plus de nouvelles conditions. Comme \(p\) et \(r\) apparaissent dans ces deux équations, on voit qu'on peut librement choisir ces deux nombres et calculer \(q\) et \(s\) en fonction d'eux. On a \(q=-p-r\) et \(s=r-p\) et, dès lors, le carré magique doit être de la forme:
| \(p\) | \(-p-r\) | \(r\) |
| \(r-p\) | \(0\) | \(p-r\) |
| \(-r\) | \(p+r\) | \(-p\) |
Pour revenir au problème initial, un carré magique de constante \(k\), il suffit d'ajouter \(e=k/3\) à tous les éléments, et on obtient:
| \(e+p\) | \(e-p-r\) | \(e+r\) |
| \(e-p+r\) | \(e\) | \(e+p-r\) |
| \(e-r\) | \(e+p+r\) | \(e-p\) |
En nous rappelant comment multiplier un carré par un nombre et comment les additionner, tout carré magique \(3×3\) peut s'écrire:
| \(e\) |
|
+ \(p\) |
|
+ \(r\) |
|
et, en particulier, l'exemple de carré magique donné plus haut peut s'écrire sous cette forme avec \(e=5\), \(p=3\) et \(r=1\).
Voila un exemple inattendu d'espace vectoriel à 3 dimensions (défini par une de ses bases).