Une des méthodes les plus courantes pour la représentation plane de figures spatiales est l'axonométrie: 3 vecteurs de base de l'espace (généralement un trièdre orthonormé) sont représentés dans le plan et permettent ainsi de dessiner tout point de l'espace à l'aide de combinaisons linéaires de ceux-ci.

Il est clair que par projection parallèle sur un plan un trièdre orthonormé se projette selon 3 vecteurs qui engendrent le plan. Ce qui est plus surprenant, c'est la réciproque (théorème de Pohlke):

Tout triple de vecteurs d'un plan peut être vu, à une homothétie près, comme la projection parallèle d'un trièdre orthonormé.

Fixons les notations: soient a, b, c les 3 vecteurs orthonormés de l'espace d'origine o et A, B, C les 3 vecteurs engendrant le plan; nous les prendrons d'origine commune O.
Remarquons tout d'abord qu'on peut exprimer l'un de ces trois vecteurs en fonction des deux autres; supposons que ce soit C = λA + μB. On en déduit, pour autant que le théorème soit vrai, que les vecteurs k(c -  λa -  μb) se projettent sur le vecteur nul. Cette observation permet de déduire que la direction de projection est celle du vecteur p = c -  λa -  μb.

La direction de projection étant déterminée, nous pouvons amener O sur la droite de direction p passant par o. Il suffira de montrer qu'on peut orienter le plan P autour de O de telle sorte que la projection du trièdre a, b, c parallèlement à p soit A', B', C' semblable à A, B, C; remarquons qu'il suffit d'ailleurs de ne s'intéresser qu'aux vecteurs A et B, étant donné que le vecteur C est lié à ces deux vecteurs par la relation C =  λA +  μB.

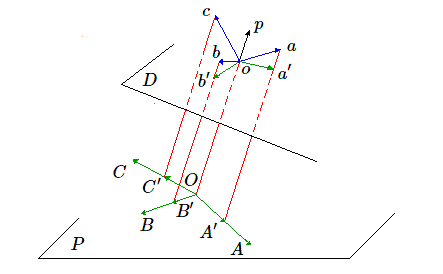
À ce stade de l'analyse, il est commode d'utiliser des coordonnées.
Pour ce faire, on choisit dans l'espace un nouveau repère dont l'un des vecteurs est dirigé selon la direction de projection. Soit D un plan perpendiculaire à p contenant les deux autres vecteurs de base de notre repère. Les deux vecteurs a et b se projettent dans D selon deux vecteurs a' et b' de coordonnées (a₁, a₂, 0) et (b₁, b₂, 0). La section par le plan P donnera deux vecteurs A' et B' de coordonnées (a₁, a₂, x) et (b₁, b₂, y).
Choisir la position du plan P revient à choisir x et y de telle manière que les vecteurs A' et B' soient semblables aux vecteurs A et B.

Les conditions s'écrivent:

De ces deux équations en x et y on tire :

Ces équations en x, y représentent dans le plan Oxy deux hyperboles centrées à l'origine: la première d'asymptotes x² = ky², la seconde d'asymptotes xy = ky²cosφ.

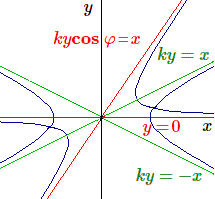
Comme -1 < cosφ < 1, il en résulte que les deux paires d'asymptotes se séparent et que les deux hyperboles se coupent en deux points symétriques (x, y) et (-x, -y).

On a donc montré que le système d'équations possède toujours des racines réelles et, par conséquent, qu'il est possible de sectionner les projetantes des vecteurs a, b parallèlement à la direction de projection p par un plan P de telle manière que les vecteurs obtenus soient semblables aux vecteurs A, B. Il en résulte que tout triple de vecteurs engendrant le plan est, à une homothétie près, la projection parallèle d'un trièdre orthonormé.

Toutefois les représentations obtenues ne sont pas les plus proches de la réalité; on peut mieux faire.