Nous savons qu'il existe une unique fonction du premier degré prenant des valeurs données pour deux valeurs distinctes de \(x\). Géométriquement, cela signifie que par deux points (d'abcisses distinctes) passe une seule droite.

De même, il existe une unique fonction polynôme du second degré prenant des valeurs données pour trois valeurs distinctes de \(x\). A nouveau, la traduction géométrique est la suivante: par 3 points d'abscisses distinctes passe une seule parabole d'axe parallèle à l'axe \(Oy\) (ou éventuellement une droite). Et ainsi de suite ...

Au plus le nombre de valeurs prédéterminées de la fonction est grande, au plus le degré du polynôme sera grand. Plus précisément, si on se donne \(N\) valeurs, le degré du polynôme vaudra \(N-1\) (voir l'article relatif aux approximations ).

Pour déterminer cette fonction polynôme, on peut partir d'un polynôme de degré \(N-1\) comportant \(N\) coefficients indéterminés et exprimer que cette fonction prend les \(N\) valeurs données. Cela conduira à un système de \(N\) équations à \(N\) inconnues qui possèdera toujours une solution unique. Nous avons utilisé cette remarque et prouvé l'unité des solutions dans l'article sur les développements en série .

Résoudre un système \(N × N\) est une solution assez lourde. Toutefois, il existe une autre méthode, bien plus simple, pour calculer ces fonctions polynomes. En effet, il suffit de remarquer que si on arrive à déterminer un ensemble de \(N\) polynômes nuls pour toutes les valeurs données de \(x\), sauf une où pour laquelle il sera égal à \(1\), on obtiendra la solution en combinant linéairement ces \(N\) polynômes. Voyons cela plus concrètement.

Soit à déterminer la fonction \(F(x)\) du premier degré en \(x\) prenant la valeur \(A\) pour \(x=a\) et la valeur \)B\) pour \(x=b\) (évidemment \(a\) et \(b\) sont différents) Calculons \(f(x)\) polynôme du premier degré, tel que \(f(a)\) = 1 et \(f(b)\) = 0. Si le polynôme s'annule pour \(x = b\), c'est qu'il est de la forme \(k(x-b)\). Pour \(x = a\) il vaut \(f(a) = k(a-b)\) = 1, d'où \(k\) = 1/(a-b)\). La fonction \(f(x)=(x-b)/(a-b)\) répond donc aux conditions. Par analogie \(g(x)=(x-a)/(b-a)\) est nulle pour \(x=a\) et prend la valeur \(1\) pour \(x=b\)

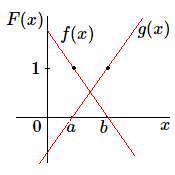
La fonction \(F(x)\) cherchée s'écrit donc:

\[F(x) = Af(x) + Bg(x)\]

Plaçons-nous dans le cas des fonctions polynômes du deuxième degré. Soit une fonction \(F(x)\) prenant les valeurs données \(A\), \(B\) et \(C\) pour les valeurs de \(x\) égales à \(a\), \(b\) et \(c\). Nous allons déterminer trois fonctions s'annulant pour deux de ces trois valeurs et valant 1 pour la troisième valeur.

Commençons par déterminer la fonction \(f(x)\) telle que \(f(a) = 1\), \(f(b)=f(c)=0\). Cette fonction s'annule pour \(x=b\) et \(x=c\) et sera donc de la forme \(f(x)=k(x-b)(x-c)\). La condition \(f(a)=1\) déterminera la constante \(k\). \(k(a-b)(a-c)=1\), d'où \(k=1/(a-b)(a-c)\)

On a ainsi déterminé la fonction :

\[ f(x)=(x-b)(x-c)/(a-b)(a-c) \]

et de même, la fonction \(g(x)\) s'annulant en \(a\) et \(c\) et valant \(1\) pour \(x=b\) sera :

\[ g(x)=(x-a)(x-c)/(b-a)(b-c) \]

Enfin, la dernière fonction que nous cherchons est \(h(x)\); elle est nulle pour \(x=a\) et \(x=b\) et elle prend la valeur \(1\) pour \(x=c\). On obtient :

\[ h(x)=(x-a)(x-b)/(c-a)(c-b) \]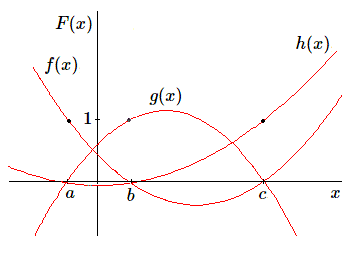

La fonction cherchée \(F(x)\) sera la combinaison linéaire des 3 fonctions calculées \(f\), \(g\) et \(h\), c'est-à-dire:

\[ F(x) = Af(x) + Bg(x) + Ch(x) \]

Remarquons que cette formule s'écrit très élégamment sous la forme:

\[ F(x)=\frac{A(x-b)(b-c)(c-x)+B(a-x)(x-c)(c-a)+C(a-b)(b-x)(x-a)}{(a-b)(b-c)(c-a)} \]

On peut procéder ainsi avec des polynômes de degré quelconque. Pour des polynômes de degré inférieur à \(n\), on sait qu'ils constituent un espace vectoriel de dimension \(n+1\); la base la plus évidente est formée des polynômes \(1, x, x^2,..., x^n\). Avec la méthode décrite plus haut, nous obtenons une autre base, mieux adaptée au problème posé.

A l'occasion de la règle de Horner , nous rencontrerons encore une autre base pour l'ensemble de ces polynômes.