Lorsqu'on commence l'étude de la géométrie, on se focalise assez rapidement sur l'étude des triangles.

Pourquoi donc ? Pourtant, lorsqu'on regarde autour de soi, la figure géométrique la plus souvent rencontrée est probablement le rectangle (portes, fenêtres, table,...) Le rectangle possède pourtant des propriétés exceptionnelles: il a deux axes de symétries (ses médianes) et un centre de symétrie (leur intersection). Bien souvent, il est utile de considérer des figures ne possédant aucune isométrie. Alors que choisir ? Un point, évidemment pas. Deux points ou un segment, c'est déjà mieux, mais cette figure possède les mêmes isométries qu'un rectangle. Alors, il faut faire un pas supplémentaire, ajouter un point extérieur au segment et on est ainsi conduit au triangle. Evidemment, il ne faut pas prendre un triangle équilatéral ou isocèle et éviter le triangle rectangle, mais prendre un triangle quelconque.

C'est la figure la plus simple ne possédant aucune isométrie (à part l'identité bien sûr).

De manière traditionnelle, on étudie des droites "remarquables" qu'on peut lui associer. Les premières que l'on rencontre sont les bissectrices, les médiatrices, les hauteurs et les médianes. Miraculeusement, chacun des triples de droites est constitué de trois droites concourantes. Comme il est exceptionnel que 3 droites données concourent en un même point, c'est ce qui justifie le qualificatif "remarquable" qu'on a associé à ces droites.

Pourtant, on s'aperçoit assez rapidement qu'un type est différent des trois autres. En effet, si l'on dessine un triangle et ses 3 bissectrices, médiatrices,... sur un carreau et que l'on regarde l'ombre portée par le soleil, on constate que, bien que l'ombre du triangle soit toujours un triangle, l'ombre d'une bissectrice n'est généralement plus une bissectrice; plus visible peut-être, l'ombre d'une médiatrice ou d'une hauteur n'est pas non plus une médiatrice ni une hauteur. On voit immédiatement que l'ombre des angles droits n'est, en général, jamais un angle droit. Par contre, les médianes d'un triangle restent des médianes. Il s'agit d'une notion affine, invariante par des transformations linéaires.

Le fait que les trois médianes d'un triangle concourent en un point, centre de masse ou barycentre, se démontre aisément .

Pour les trois autres types de droites remarquables, on utilise des propriétés métriques. Le fait que médiatrices ou bissectrices soient concourantes résulte du fait qu'une médiatrice est axe de symétrie d'un segment et qu'une bissectrice est axe de symétrie d'un angle. En ce qui concerne les hauteurs, c'est un peu moins immédiat.

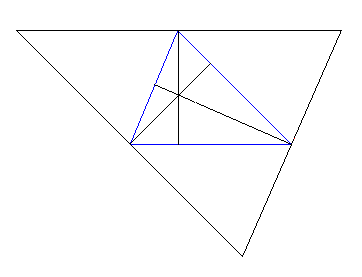
D'habitude, par chacun des 3 sommets du triangle, on trace la parallèle au côté opposé et les hauteurs du petit triangle initial deviennent les médiatrices du triangle formé par les 3 droites et il en résulte qu'elles sont concourantes. Comme médiatrices et bissectrices ont des propriétés fort semblables, n'y aurait-il pas moyen de trouver un lien entre hauteurs d'un triangle et bissectrices d'un nouveau triangle ?

Partons d'un triangle et de ses trois bissectrices que nous savons concourantes. Par chaque sommet du triangle, passe une bissectrice. Construisons la perpendiculaire et remarquons qu'en fait, il s'agit de la bissectrice extérieure de l'angle.

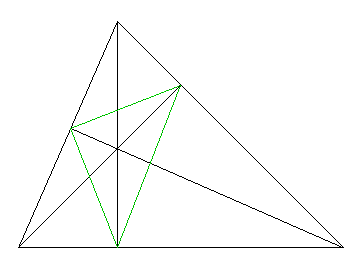
Mais la bissectrice d'un angle et les bissectrices des deux autres angles sont également concourantes et par conséquent, les bissectrices du triangle initial deviennent les hauteurs du triangle formé par les 3 perpendiculaires aux 3 bissectrices.

Inversement, partons du triangle \(ABC\). Notons \(A',B'\) et \(C'\) les points où les hauteurs coupent respectivement \(BC,CA\) et \(AB\). Traçons les deux cercles de diamètre \(AB\) et \(AC\).

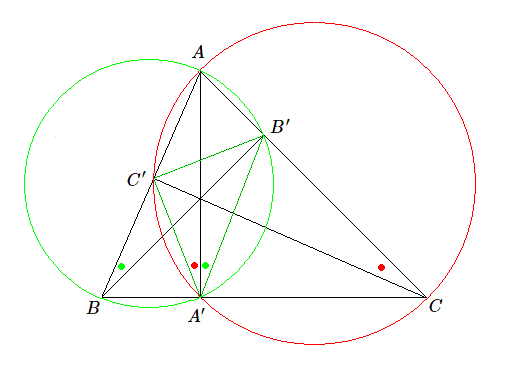
Le cercle de diamètre \(AB\) passe par \(A'\) et \(B'\) et les deux angles inscrits \(ABB'\) et \(AA'B\) sont égaux car ils interceptent le même arc \((AB)\). De même, le cercle de diamètre \(AC\) passe par \(A'\) et \(C'\) et les deux angles inscrits \(ACC'\) et \(AA'C\) sont égaux car ils interceptent le même arc \((AC)\). Ces angles sont tous égaux à \(90°- BAC\) et \(AA'\) est donc la bissectrice de l'angle \(C'A'B'\). On peut raisonner de même pour les autres sommets \(B'\) et \(C'\). Le triangle \(A'B'C'\) (appelé parfois triangle orthique du triangle \(ABC\)) admet donc les hauteurs du triangle \(ABC\) comme bissectrices.

Dans chacune des constructions décrites ci-dessus, on peut évidemment montrer que si on part du "grand" triangle, on retombe sur le "petit" triangle initial.

En résumant les observations faites plus haut, on obtient une jolie figure formée par 3 triangles emboîtés et 3 droites concourantes. Les médiatrices du grand triangle sont les hauteurs du deuxième triangle et les bissectrices du petit triangle.