On a coutume de dire: "La droite est le chemin le plus court d'un point à un autre".

C'est peut-être vrai dans le plan, mais qu'en est-il sur une sphère ? Y a-t-il des droites sur une sphère ? Bien sur que non, mais il y a des plus courts chemins. On peut s'en convaincre en choisissant 2 points sur une mappemonde et en tendant une ficelle entre eux. Elle se positionnera en épousant la trajectoire d'un arc de grand cercle (cercle obtenu en sectionnant la sphère par un plan passant par le centre). Pourquoi est-il important de connaître ce plus court chemin ? Tout simplement parce que la forme de la Terre est très proche de celle d'une sphère et que la durée et le prix d'un trajet en avion sont fortement influencés par la distance parcourue.

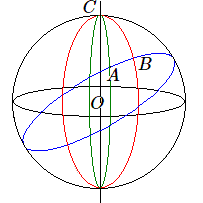
Essayons de calculer la distance entre deux villes représentées par les points A et B d'une sphère. Généralement, on repère un lieu par sa latitude \(\alpha \) et sa longitude \(\lambda \). Toutefois, il est plus commode d'utiliser la colatitude en lieu et place de la latitude. La colatitude est mesurée à partir d'un pôle (le pôle Nord) que nous désignerons par C; elle prend des valeurs de l'intervalle [0°, 180°] (ou [0, \(\pi \)] car le mathématicien préfère toujours convertir les degrés, minutes et secondes en radians (unité plus commode à utiliser). Dans l'hémisphère nord, c'est le complément de la latitude et dans l'hémisphère sud, c'est la latitude augmentée de 90°. Désignons cette colatitude par \(\beta \).

A présent, choisissons le rayon (moyen) de la Terre comme unité de longueur et considérons la sphère de rayon 1. Nous choisirons un repère orthonormé \(Oxyz\) avec \(Ox\) et \(Oy\), deux axes situés dans le plan de l'équateur. Nous choisirons \(Ox\) dirigé vers le méridien de Greenwich. L'axe \(Oz\) sera l'axe OC, axe de rotation de la Terre.

Quelles sont, dans ce repère, les coordonnées du point P de longitude \(\lambda \) et de colatitude \(\beta \) ?

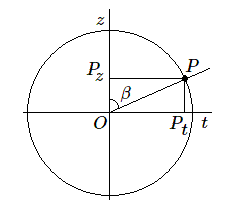
La coordonnée \(z\) du point \(P\) est tout simplement égale à \(\mathbf{cos~}\beta\). Quant aux coordonnées \(x\) et \(y\), elles sont les projections de \(\mathbf{sin~}\beta\) respectivement sur le plan de longitude \(0\) et de longitude 90°ou \(π/2\). on a donc \(x_P=\mathbf{sin~}\beta.\mathbf{cos~}\lambda \) et \(y_P=\mathbf{sin~}\beta.\mathbf{sin~}\lambda \) Appliquons ce résultat aux points \(A\) et \(B\). On obtient :

\[ (x_A,y_A,z_A)=(\mathbf{sin~}\beta_A.\mathbf{cos~}\lambda_A,\mathbf{sin~}\beta_A.\mathbf{sin~}\lambda_A,\mathbf{cos~}\beta_A) \]

et une expression analogue pour B.

Pour mesurer l'arc \(AB\), il suffit de remarquer que le produit scalaire des vecteurs \(OA\) et \(OB\) vaut \(\mathbf{cos~}AB\):

\[ \small \mathbf{cos~}AB=\mathbf{sin~}\beta_A.\mathbf{cos~}\lambda_A.\mathbf{sin~}\beta_B.\mathbf{cos~}\lambda_B +\mathbf{sin~}\beta_A.\mathbf{sin~}\lambda_A.\mathbf{sin~}\beta_B.\mathbf{sin~}\lambda_B +\mathbf{cos~}\beta_A.\mathbf{cos~}\beta_B \]

En regroupant les deux premiers termes, on peut mettre \(\mathbf{sin~}\beta_A.\mathbf{sin~}\beta_B\) en facteur et le coefficient n'est autre que le cosinus de la différence des longitudes. On a:

\[\mathbf{cos~}AB=\mathbf{sin~}\beta_A.\mathbf{sin~}\beta_B\mathbf{cos~}(\lambda_A-\lambda_B)+\mathbf{cos~}\beta_A\mathbf{cos~}\beta_B \]

Connaissant le \(\mathbf{cos~}AB\) et donc l'angle \(AB\) ainsi que la valeur du rayon terrestre (environ 6375 km) que nous avions pris comme unité, la distance des villes \(A\) et \(B\) est connue. Tous calculs faits, on se rend compte que la contribution importante provient la différence de longitude des deux villes.

Prenons un exemple concret \(A\) = Paris (48°48' N, 2°20' E) et \(B\) = Tokyo (35°40'N, 139°45'E). En utilisant les valeurs décimales en degrés, on obtient pour colatitude \(\beta\) et longitude \(\lambda\): Paris (41.2, 2.333...) et Tokyo (54.333..., 139.75); la distance Paris-Tokyo vaut à peu près 9723 km.

Il est intéressant de tracer le trajet sur un planisphère; on obtient:

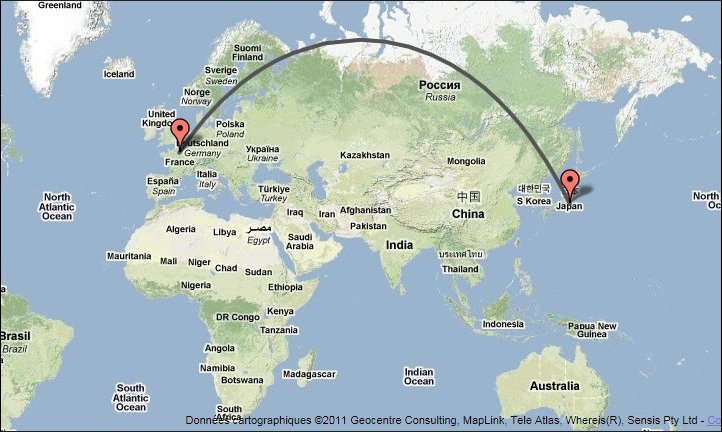
Cette figure illustre bien l'impossibilité de représenter fidèlement la Terre (une sphère) sur une carte (un plan) quel que soit le mode de projection utilisé. Signalons que la projection gnomonique (projection à partir du centre sur un plan) fait apparaître les plus courts chemins comme des droites, mais il y a déformation des distances.

Reprenons le problème résolu plus haut.

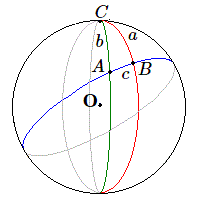Le schéma utilisé représentait les deux villes \(A\) et \(B\) ainsi que le pôle Nord \(C\) et ces trois points reliés par des arcs de grands cercles déterminaient, sur la sphère, un triangle. L'axe de la Terre et l'équateur n'étaient présents que pour justifier le choix du système de coordonnées. Débarrassons-nous de ces éléments superflus afin de mieux comprendre le problème que nous avons résolu. Il nous reste sur une sphère de centre \(O\), les trois points \(A\), \(B\) et \(C\) ainsi que trois grands cercles qui les relient deux à deux. Ces trois points \(A\), \(B\) et \(C\) ainsi que les trois arcs \(a, b, c\) de grands cercles qui les relient constituent un triangle sphérique . Cette figure est l'analogue sur la sphère d'un triangle du plan.

Relevons toutefois quelques différences importantes avec les triangles du plan: - Les côtés ne sont pas des segments de droites mais des arcs de grands cercles; ils possèdent donc une mesure, celle de l'angle interceptant l'arc. - La somme des angles d'un triangle n'est pas fixe; plus le triangle est grand, plus la somme des angles dépasse π (ou 180°).

Quant au problème que nous avons résolu plus haut, nous avons calculé le côté \(c\) en fonction des deux autres côtés \(a\) et \(b\) (donnés par leur colatitude) et de l'angle compris \(C\) (la différence des longitudes). La formule obtenue s'écrit :

\[ \mathbf{cos~}c=\mathbf{cos~}a.\mathbf{cos~}b+\mathbf{sin~}a.\mathbf{sin~}b.\mathbf{cos~}C\]

Nous pouvons évidemment écrire deux formules analogues donnant le cosinus de chacun des deux autres côtés en fonction des deux autres côtés et de l'angle compris.

De cette formule, nous tirons la valeur de \(\mathbf{cos~}C\) :

\[ \mathbf{cos~}C=\frac{\mathbf{cos~}c-\mathbf{cos~}a.\mathbf{cos~}b}{\mathbf{sin~}a.\mathbf{sin~}b} \]

Calculons à présent la valeur de \(\mathbf{sin~}C\); le calcul est simple mais un peu long. Toutefois le résultat en vaut la peine. On a:

$$ \begin{align} \mathbf{sin~}^2C = & 1-\frac{(\mathbf{cos~}c-\mathbf{cos~}a.\mathbf{cos~}b)^2}{\mathbf{sin~}^2a.\mathbf{sin~}^2b}=\frac{\mathbf{sin~}^2a.\mathbf{sin~}^2b-(\mathbf{cos~}c-\mathbf{cos~}a.\mathbf{cos~}b)^2}{\mathbf{sin~}^2a.\mathbf{sin~}^2b}\\ & =\frac{(1-\mathbf{cos~}^2a)(1-\mathbf{cos~}^2b)-(\mathbf{cos~}c-\mathbf{cos~}a.\mathbf{cos~}b)^2}{\mathbf{sin~}^2a.\mathbf{sin~}^2b} \\ & =\frac{1-\mathbf{cos~}^2a-\mathbf{cos~}^2b-\mathbf{cos~}^2c+2\mathbf{cos~}a.\mathbf{cos~}b.\mathbf{cos~}c}{\mathbf{sin~}^2a.\mathbf{sin~}^2b} \end{align} $$

Le numérateur est symétrique en \(a, b\), et \(c\). En divisant le résultat obtenu par \(\mathbf{sin~}^2c\), nous rendons le dénominateur également symétrique en les trois côtés :

\[ \frac{\mathbf{sin~}C^2}{\mathbf{sin~}c^2}=\frac{1-\mathbf{cos~}^2a-\mathbf{cos~}^2b-\mathbf{cos~}^2c+2\mathbf{cos~}a.\mathbf{cos~}b.\mathbf{cos~}c}{\mathbf{sin~}^2a.\mathbf{sin~}^2b.\mathbf{sin~}c^2} \]

et comme tous les angles ont un sinus positif, nous pouvons finalement écrire:

\[ \frac{\mathbf{sin~}A}{\mathbf{sin~}a}=\frac{\mathbf{sin~}B}{\mathbf{sin~}b}=\frac{\mathbf{sin~}C}{\mathbf{sin~}c} \]

Les formules du cosinus trouvées plus haut ainsi que la formule des sinus sont les formules essentielles de la trigonométrie sphérique.

Plus amusant ! À tout triangle, on peut associer un triangle polaire. À chaque sommet \(S\), on associe le plan \(s\) perpendiculaire au vecteur \(OS\) et à chaque côté \(c\) le vecteur perpendiculaire \(OC\). Le nouveau triangle construit est le polaire et, par définition même, le polaire du polaire est le triangle initial. La construction décrite est telle que les angles et les côtés du triangle polaire sont respectivement égaux aux cotés et aux angles du triangle de départ. La formule démontrée plus haut peut alors être appliquée au triangle polaire; il suffit de permuter angles et côtés.

"Mais que c'est compliqué tout cela ! Quand je me déplace en Belgique, je peux tout simplement mesurer les distances sur une carte." me direz-vous. En effet, il n'y aura guère de différence dans les résultats trouvés car la Terre est tellement grande qu'on peut considérer qu'un petit pays, un petit morceau de sphère, est presque un morceau de plan. En particulier, un petit triangle sphérique ressemblera très fort à un triangle plan. Les angles \(a, b, c\) correspondant aux côtés sont tellement petits qu'on pourra faire une approximation et, comme on le fait souvent en physique, assimiler \(\mathbf{sin~}a\) à \(a\).

Et \(\mathbf{cos~}a\), que devient-il ? On appliquera les approximations suivantes:

$$ \mathbf{sin~}a\approx a, ~~~~~~\mathbf{cos~}a=\sqrt{1-\mathbf{sin~}^2a}\approx 1-\frac{a^2}{2} $$ $$ \mathbf{cos~}a.\mathbf{cos~}b\approx (1-\frac{a^2}{2})(1-\frac{b^2}{2})\approx 1-\frac{a^2+b^2}{2} $$

car on peut oublier le terme en \(a^2 b^2\).

Remplaçons dans la formule \(\mathbf{cos~}c=\mathbf{cos~}a.\mathbf{cos~}b+\mathbf{sin~}a.\mathbf{sin~}b.\mathbf{cos~}C\), les sinus et cosinus des côtés par une approximation et nous obtiendrons:

\(c^2=a^2+b^2-2ab.\mathbf{cos~}C\), c'est-à-dire la formule d'Al-Kashi.

Pour la formule des sinus cela donnera:

\[ \frac{\mathbf{sin~}A}{a}=\frac{\mathbf{sin~}B}{b}=\frac{\mathbf{sin~}C}{c} \]

On retrouve ainsi les formules de base de trigonométrie plane.