Propriétés affines
Tout d'abord remarquons qu'en général, une conique possède un centre de symétrie ; il se trouve au milieu de tous les diamètres, ou encore ses conjugués harmoniques sont tous à l'infini .
- Le centre d'une conique a pour polaire la droite de l'infini (la réciproque est-elle vraie ?).
- Un diamètre est le pôle d'un point à l'infini.
- Deux diamètres seront dits conjugués si leurs points à l'infini le sont.
- Enfin une tangente à l'infini sera appelée asymptote
Soit tout d'abord un triangle autopolaire formé de deux sécantes et d'une non sécante.

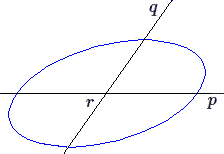
- Si la droite non sécante est la droite de l'infini, la conique est une ellipse, \(r\) est son centre ; \(pr\) et \(qr\) sont deux diamètres conjugués.
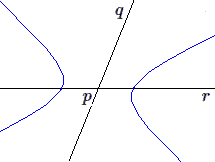
- Si au contraire c'est une sécante (par exemple \(qr\)) qui est la droite de l'infini, la conique est une hyperbole centrée en \(p\) rapportée à deux diamètres conjugués \(pq\) et \(pr\).
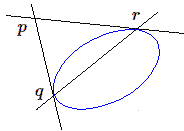
Soit à présent un triangle autopolaire formé de deux tangentes et de la corde de contact.
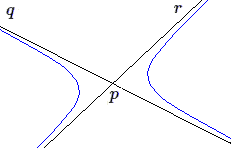
- Si la sécante \(qr\) est la droite de l'infini, la conique est une hyperbole centrée en \(p\) et les deux tangentes aux points \(q\) et \(r\) à l'infini sont les deux asymptotes.
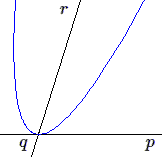
- Si au contraire c'est une tangente (par exemple \(pq\)) qui est la droite de l'infini, la conique est une parabole ramenée à une tangente \(pr\) et à son diamètre conjugué \(qr\).
Propriétés euclidiennes
Si l'on désire étudier quelques propriétés euclidiennes, il suffit d'introduire la métrique (ou le produit scalaire). Il n'y a aucune difficulté à résoudre alors tous les problèmes.
A titre d' exemple , sans toutefois attacher d'importance particulière à ce théorème qui relève plutôt des curiosités mathématiques, pour montrer la puissance des résultats généraux obtenus, citons la détermination de l'ensemble des points desquels on voit une ellipse sous un angle droit, le très "classique" cercle de Monge appelé encore cercle orthoptique.
En considérant l'ensemble des cercles on est conduit à parler des points (imaginaires à l'infini) cycliques. On remarque alors que deux directions sont perpendiculaires si leurs points à l'infini sont conjugués par rapport aux points cycliques (lien entre une forme quadratique et la forme bilinéaire associée).
Après avoir introduit les conditions d'orthogonalité, il n'est plus guère difficile de rechercher les axes (de symétrie) d'une conique ainsi que les foyers et directrices.
Conclusion
On en conclut qu'une étude générale (propriétés projectives) des coniques permet un énorme gain de temps pour l'étude détaillée de chacun des types affins de coniques (ellipses, paraboles et hyperboles).