Construction des polyèdres étoilés de Kepler-Poinsot
|
Pour ceux qui souhaitent construire ces beaux objets, nous donnons ci-dessous quelques indications. Plusieurs solutions sont possibles:
Nous vous donnons les meilleurs patrons (trouvés sur le site http://www.korthalsaltes.com). Grand dodécaèdre étoilé
La partie visible d'une face est formée de 5 petits triangles isométriques qui constituent les "pointes" d'un pentagone étoilé Le patron s'obtient alors de manière fort simple. 
Pour réaliser un modèle de petite taille de rigidité suffisante, nous vous conseillons plutôt de partir d'un icosaèdre et de coller sur ses 20 faces des petites pyramides dont les faces latérales sont des triangles correspondant aux parties visibles des faces. Petit dodécaèdre étoilé
La partie visible d'une face est formée de 5 petits triangles isométriques qui constituent les "pointes" d'un pentagone étoilé. Le patron s'obtient alors de manière fort simple. 
Pour réaliser un modèle de petite taille de rigidité suffisante, nous vous conseillons plutôt de partir d'un dodécaèdre et de coller sur ses 12 faces des petites pyramides dont les faces latérales sont des triangles correspondant aux parties visibles des faces. Grand dodécaèdre
La partie visible d'une face pentagonale est le pentagone amputé du pentagone étoilé correspondant. Sur chaque face du grand dodécaèdre, on trouve une étoile à 5 branches possédant 10 facettes isométriques dont on voit ainsi la taille réelle. 
Le patron s'obtient alors de manière fort simple. Pour pouvoir être aisément utilisé, le patron doit être agrandi mais cette fois, il conduit à un résultat acceptable s'il est assemblé avec grand soin. Une méthode plus aisée consiste à assembler 10 éléments formés chacun de deux "creux" tels que représentés sur la figure. Grand icosaèdreAfin de construire ce polyèdre, un peu plus compliqué que les autres, on peut essayer de reconstituer la partie visible d'une face triangulaire. 
Cette partie est formée de 9 triangles; les 6 triangles passant par les sommets sont isométriques et 3 autres également. En voici un schéma représentant la situation décrite ci-dessus. On remarque que les points de subdivision des côtés sont tels que le rapport des 3 petits segments aux 6 grands est précisément le nombre d'or τ = ½ ( 
La méthode la plus efficace pour un modèle de petite taille semble être la réalisation de 12 petites "pyramides étoilées" qu'on assemble ensuite (ne pas oublier de prévoir des tenons !). |

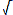 5 - 1).
Il est alors aisé de contruire un
5 - 1).
Il est alors aisé de contruire un