Voici quelques exemples où apparaît la notion de limite, les deux premiers font partie de la "culture générale", les deux suivants sont moins courants mais font partie de la vie courante et le dernier attire l'attention sur les dangers d'une intuition non contrôlée.
La tortue
Chacun connaît le paradoxe d'Achille et de la tortue. Achille court 10 fois plus vite que la tortue, mais elle possède 10 mètres d'avance sur lui. (Peut-être n'était-ce pas 10 mètres, mais 10 stades, mais qu'importe) Il est clair qu'Achille ne la rattrapera jamais ! En effet, quand il aura parcouru 10 mètres, la tortue aura avancé d'un mètre. Si Achille parcourt ce mètre, la tortue aura encore avancé de 10 cm et ainsi de suite. Donc Achille ne la rattrapera jamais.
La flèche
De même on cite souvent le paradoxe de Zénon. Une flèche lancée n'atteindra jamais son but! En effet, pour y arriver, elle devra parcourir la moitié du trajet. Quand elle y sera arrivée, elle devra parcourir la moitié du trajet restant et ainsi de suite, indéfiniment. Donc une flèche n'atteint jamais son but.
Le gâteau
Pour fêter la réussite de son examen de math, Natacha a apporté un splendide gâteau qu'elle veut partager avec son frère Olivier. Olivier, qui se sert le premier (et est gourmand !), prend la moitié du gâteau. Natacha, remplie de scrupules (ou qui veut garder sa ligne ?), n'ose pas prendre ce qui reste; elle ne prend que la moitié du reste (le quart) et chacun déguste sa portion. En veux-tu encore un peu, demande Natacha. Bien sur, répond Olivier et il prend la moitié du reste. Natacha, qui dans le fond n'a pas tellement faim, prend la moitié de ce qui reste. Et le petit jeu continue...
En fait qu'ont mangé chacun des deux ? Facile, dit Natacha qui est forte en math ; il suffit de faire la somme de nos parts, c'est-à-dire:

Dans les deux cas il s'agit d'une progression géométrique de raison 1/4 et il me semble bien avoir vu une formule qui donnait la somme des termes d'une telle progression. Malheureusement je ne m'en souviens plus. Mais cela n'a pas d'importance, dit-elle à son frère, de toutes façons tu n'y comprendrais rien, tu n'as pas revu les limites.
C'est vrai, dit Olivier, mais à chaque fois j'ai mangé le double de toi, n'est-ce pas? Dès lors puisque nous avons terminé le gâteau j'en ai mangé les deux tiers et toi un tiers. Qu'en penses-tu ?
Promotion
Un fabricant de desserts savoureux (y en a-t-il d'autres?) a lancé une campagne promotionnelle. Chaque dessert est accompagné d'un point. Quatre points donnent droit à un dessert gratuit. Cela constitue une manière déguisée et ludique d'offrir une réduction. Mais au fait à combien se monte cette réduction ? Une première réponse, intuitive, consiste à dire qu'avec 4 desserts achetés, on obtient 4 points donc un des 4 desserts est gratuit. Il y a donc une réduction de 25%.
Supposons que le prix d'achat d'un dessert soit N. Puisqu'il nous faut quatre points pour obtenir un dessert gratuit, nous grouperons nos achats par 4.
| Nombre de desserts | Prix total | Prix unitaire |
|---|---|---|
| 4 | 4N | N |
| 8 | 8N - N = 7N | 7/8.N |
| 12 | 12N - 2N = 10N | 5/6.N |
| 16 | 16N - 3N = 13N | 13/16.N |
| ... | ... | ... |
| 4 k | 4 k N - ( k - 1)N = (3 k - 1)N | (3 k - 1)/4 k .N |
On voit ainsi que la réduction n'est pas de 25%, mais tend vers cette valeur. Au plus vous en mangerez, au plus la réduction sera forte. Bon appétit !
De moins en moins, de plus en plus
Soit la somme 1 + 1/2 + 1/3 + 1/4 + 1/5+... Combien vaut sa limite ?
Cette série est appelée série harmonique . Il semble " évident " que l'on ajoute quelque chose de plus en plus petit, et qu'à la limite on obtiendra une valeur bien déterminée. Un exemple concret est donné par la situation suivante: On pose une brique. Sous cette brique on dépose une deuxième brique que l'on décale le plus possible (son centre de gravité de la première doit reposer sur la deuxième et elle ne peut donc être décalée que de la moitié d'une brique. Prenons cette distance comme unité. On pose ensuite sous l'ensemble une troisième brique que l'on décale le plus possible. Attention, il faut cette fois que le centre de gravité de l'ensemble des deux briques repose sur la troisième; on ne peut plus la décaler que d'1/2 unité. Continuons à poser sous l'ensemble une quatrième brique que nous décalons le plus possible.
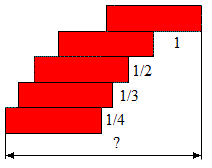 De combien pouvons-nous décaler la troisième brique ?
Choisissons pour origine l'extrémité de la troisième brique et pour unité une demi-brique; calculons la coordonnée du centre de gravité des trois premières briques. Le centre de gravité des deux premières a pour coordonnée 0 (nous sommes en équilibre au-dessus de la troisième brique) et celui de la troisième a pour coordonnée 1. L'abscisse du centre de gravité de l'ensemble aura pour coordonnée (2.0 + 1.1)/3 = 1/3. Nous pourrons décaler l'ensemble des 3 briques d'une distance égale à 1/3.
De combien pouvons-nous décaler la troisième brique ?
Choisissons pour origine l'extrémité de la troisième brique et pour unité une demi-brique; calculons la coordonnée du centre de gravité des trois premières briques. Le centre de gravité des deux premières a pour coordonnée 0 (nous sommes en équilibre au-dessus de la troisième brique) et celui de la troisième a pour coordonnée 1. L'abscisse du centre de gravité de l'ensemble aura pour coordonnée (2.0 + 1.1)/3 = 1/3. Nous pourrons décaler l'ensemble des 3 briques d'une distance égale à 1/3.
Nous pouvons généraliser le calcul qui précède. Supposons que nous ayons superposé n briques. Calculons la coordonnée du centre de gravité en choisissant pour origine l'extrémité de la dernière brique (la n -ème). Sa coordonnée vaudra (( n - 1).0 + 1.1)/ n = 1/ n . L'ensemble pourra donc être décalé de 1/ n . Les briques vont de moins en moins se décaler et il est clair qu'elles ne pourront se décaler au-delà de toute limite sous peine de faire effondrer l'édifice.
Et pourtant...
On peut remplacer dans cette somme certains termes par des termes plus petits; cela ne fera que diminuer la valeur. Remplaçons 1/3 par 1/4, 1/5, 1/6 et 1/7 par 1/8 et ainsi de suite pour nous ramener à une somme de fractions dont le dénominateur est une puissance de 2. La somme:
est supérieure à la somme:
qui tend manifestement vers l'infini.
Il faut se méfier des apparences !