Après un bref exposé sur le calcul intégral et quelques exemples élémentaires, le professeur dit : "Voici un petit exercice de calcul intégral ; essayez de le résoudre pour demain". Calculez : \[ \int \mathbf{sin~}x.\mathbf{cos~}x.~dx \]
Alice et Bernard, les deux "forts en maths" de la classe, après quelques instants de réflexion, disent à l'unisson : "Mais enfin, c'est trop simple ; j'ai déjà trouvé". Comment fais-tu ? demande Alice à Bernard. Et ce dernier écrit sur un bout de papier:
La dérivée de \( \mathbf{sin~}x \) est \( \mathbf{cos~}x \) et, par conséquent, \( \mathbf{cos~}x.dx = d~\mathbf{sin~}x \). Si je pose \( \mathbf{sin~}x = y \), l'intégrale s'écrit: \( \int y.dy \) et le résultat vaut \( y^2/2 \) c'est-à-dire \( (\mathbf{sin~}^2x)/2. \)
Tiens, dit Alice, je l'ai fait mentalement mais je n'ai pas le même résultat !
Tu te trompes certainement, dit Bernard, très sûr de lui.
Pas du tout, répond Alice. D'ailleurs, je n'ai pas besoin de papier pour te l'expliquer : si je multiplie par \( 2 \), j'obtiens \( \int 2~\mathbf{sin~}x~\mathbf{cos~}x.dx \) et donc \( \int \mathbf{sin~}2x. dx \). En multipliant de nouveau par 2, j'obtiens \( \int \mathbf{sin~}2x.d~2x \) ce qui vaut \( -\mathbf{cos~}2x \). Et maintenant, il suffit de diviser par 4 ; le résultat final est donc \( -(\mathbf{cos~}2x)/4 \).
Pas possible, dit Bernard. Tu peux vérifier mon calcul. Dis-moi où est la faute ?
Alice, après avoir relu, dit à Bernard : En effet c'est juste mais pourtant je connais bien mes formules de trigonométrie et je suis certaine d'avoir raison.
Finalement la discussion se calme. Alice et Bernard se mettent d'accord pour demander au professeur d'expliquer ce mystère.
Le lendemain, les autres élèves ont discuté et sont d'accord, les uns avec Alice, les autres avec Bernard. Évidemment le professeur est assailli par "la question" : Qui a raison ?
Avec un grand sourire, le professeur répond : "Tout le monde !" et d'un seul coup l'excitation retombe. Enfin, comment est-il possible de trouver deux réponses différentes. On n'a jamais vu cela ! C'est vrai, mais pourtant c'est ainsi. Dans les problèmes que nous avons résolus jusqu'à présent, il y avait presque toujours une seule réponse. Mais, réfléchissez un instant, demande le prof ; quand on prend deux droites d'un plan, l'intersection est, en général, un point. Mais il se peut qu'elles soient parallèles ou même confondues. Quelque chose d'analogue se produit dans la résolution des systèmes d'équations. Si je vous demande en combien de points une droite coupe un cercle, il y a aussi plusieurs réponses différentes. Donc, vous devez effacer de votre cerveau qu'une question possède toujours une réponse unique.
Bien, maintenant examinons les deux réponses :
Bernard trouve : \( (\mathbf{sin~}^2~x)/2.\) et Alice : \( -(\mathbf{cos~}2x)/4 \)Toi, Alice qui connaît bien tes formules, quelle est la différence entre les deux ? Il y a un sinus et dans l'autre un cosinus.
D'accord, mais peux-tu me calculer la différence entre les deux ?
Je vais utiliser la formule \( \mathbf{cos~}2x = 1-2 \) \( \mathbf{sin~}^2 x \) et j'obtiens \( 1/4 \). Bon ! \( 1/4 \) ce n'est pas grand chose, mais il y a quand même une erreur quelque part.
Eh bien, non, tu as bien calculé, mais si tu te rappelles ce que j'avais expliqué hier, en dérivant le résultat, tu dois retrouver la fonction que tu viens d'intégrer. Or, la dérivée d'une constante vaut \( 0 \). Il n'y a donc aucune erreur dans vos résultats.
Je vais donc bien reprendre ce que j'avais expliqué rapidement hier. L'an dernier, nous avons appris comment calculer la dérivée d'une fonction . D'abord la dérivée des puissances, des fonctions algébriques et enfin des fonctions plus curieuses, goniométriques ou exponentielles.
Quand deux fonctions \( f(x) \) et \( g(x) \) sont dérivables, leur somme \( f(x)+g(x) \) l'est également ; de même tout multiple \( a.f(x) \) l'est aussi. Les fonctions dérivables \( F \) forment donc un espace vectoriel et il existe une application dérivée envoyant les fonctions de \( F \) sur leurs dérivées. Hier, je vous ai expliqué qu'on pouvait s'intéresser à l'application dérivée qui est en quelque sorte l'application inverse : ici, nous connaissons la dérivée, mais nous voudrions trouver toutes les fonctions dont elle provient. Il suffit de connaître l'image inverse de \( 0 \). Si la dérivée est nulle, cela signifie la fonction est constante. Dès lors, toutes les fonctions qui ne différent entre elles que par une constante ont la même image. Toute fonction de cet ensemble est appelée primitive de la fonction de départ. Si \( f(x) \) est une primitive, toutes les primitives sont de la forme \( f(x)+k \).
Un petit exemple pour mieux comprendre : Soit une fonction dont la dérivée est \( 2x \). Géométriquement, cela signifie qu'en chaque point \( (x,y), \) la pente de la tangente est connue et vaut \( 2x \). Nous obtenons, dans le plan, ce que les physiciens appellent un champ de vecteurs tangents.
Partant d'un point quelconque, on peut essayer de se représenter la courbe correspondant à la fonction. En ce premier point, on connaît la direction de la tangente en ce point et on peut ainsi tracer, de manière approximative un arc de la fonction. À l'extrémité de cet arc, on recommence l'opération et ainsi, de proche en proche, on aboutit à un tracé approximatif de la courbe. Pour s'approcher de la courbe exacte, il faudra prendre des intervalles de plus en plus petits. Dans de rares cas, à l'aide d'autres outils, on obtiendra directement l'équation d'une des courbes.
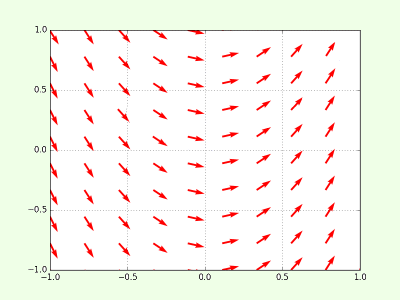
Dans ce cas simple, on peut voir que la courbe d'équation \( y = x^2 \) répond à la question. On dit qu'il s'agit d'une primitive . Dès qu'une primitive est obtenue, toutes les autres s'obtiennent en lui ajoutant une constante quelconque. En effet, les vecteurs tangents ne dépendent que de l'abscisse. Ils sont donc invariants pour les translations parallèles à l'axe des \( y \).
Dès qu'une primitive est connue, on en connaît automatiquement une famille : celles obtenues par translation parallèlement à l'axe des \( x \) c'est-à-dire \( F(x) + k \) ou dans notre exemple : \( y = x^2 + k \), avec \( k \) constant.
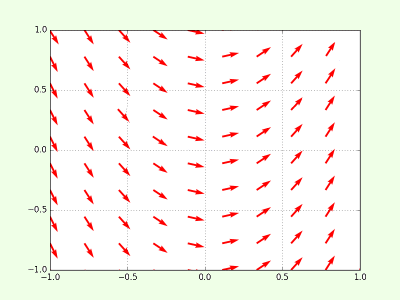
En fait, nous voyons qu'Alice et Bernard ont chacun calculé une primitive de \( \mathbf{sin~}x.\mathbf{cos~}x \) et leurs résultats sont tous les deux exacts.
A quoi peuvent bien servir toutes ces fonctions ? En mathématiques, mais aussi et surtout en physique, le champ de vecteurs donne la modification de la situation initiale dans un intervalle de la variable (en physique, souvent un intervalle de temps). On parle alors d'une intégrale définie dans l'intervalle \( a,b \). Elle s'obtient en prenant une primitive et en calculant sa variation entre \( a \) et \( b \). Comme la primitive ne diffère d'une autre que par une constante, le résultat est le même quelle que soit celle choisie. On parle alors de l'intégrale de \( a \) à \( b \) et on note \( \int_{a}^{b} f(x) \).
Attention ! Par abus de langage, certains désignent par intégrale une (article indéfini) primitive ; mais dans ce cas n'oubliez jamais la constante.