Nous avons rencontré les coordonnées trilinéaires et nous les avons notamment utilisées en diététique . Prenons donc l'exemple des valeurs énergétiques des aliments.

Sur la plupart des emballages figure la composition (pour 100g) en protides, lipides, glucides ainsi que la valeur énergétique en Kcal. Cette dernière valeur se calcule évidemment à partir des quantités de protides, lipides et glucides. Il suffit de connaître les valeurs énergétiques \(P,L,G\) (en kilocalories) de 1g de chacune des trois substances. Mais, comment les connaître ?.. Trois inconnues, donc trois équations (indépendantes si possible !). Choisissons trois produits.

Comme je suis occupé à me préparer des spaghetti, je prends la bouteille d'huile et je trouve, ce qui était évident, qu'il n'y a ni glucides, ni protides; \(100 g\) d'huile donnent \(900Kcal\), donc voila déjà un problème réglé. Un gramme de lipides contribue à raison de \(9 Kcal\). On a déjà \(L=9\)

Sur la viande aucune indication.

Passons à la sauce tomate et nous trouvons la composition suivante: \(1,3 g\) de protides, \(3,9 g\) de glucides, \(0,0 g\) de lipides; valeur énergétique \(20 Kcal\). L'équation est donc \(1,3P + 3,9G = 20\)

Pour les pâtes, nous trouvons: \(13 g\) de protides, \(1,5 g\) de lipides et \(71 g\) de glucides, pour une valeur énergétique de \(350 Kcal\). Voici notre troisième équation: \(13P + 1,5L + 71G = 350\) que nous pouvons transformer, sachant que \(L=9\), \(13P + 71G = 336,5\)

Nous avons donc un système de deux équations à deux inconnues:

\[ 1,3P + 3,9G = 20 \\ 13P + 71G = 336,5 \]

Nous avons beaucoup de chance; en multipliant la première équation par 10 et en la soustrayant de la seconde on a: \(32G = 136,5\), d'où \(G = 273/64\) et en remplaçant \(G\) par sa valeur dans l'une des deux équations on trouve \(P= 2153/832\). On obtient donc la solution: \(P=2153/832, L=9, G=273/64\) (Notons au passage qu'on ne résout pas un système, on le remplace par un système équivalent plus simple )

A tout hasard prenons un autre produit pour vérifier; par exemple des tortellini (encore des pâtes !) Pour \(100 g\) il y a \(16 g\) de protides, \(13 g\) de lipides et \(53 g\) de glucides dont la valeur énergétique vaut \(393 Kcal\). Vérifions: \(16.2153/832 + 13*9 + 53.273/64\) soit environ \(384 Kcal\).

Que se passe-t-il ? Les fabricants sont-ils des charlatans ? Les mathématiques sont-elles inconsistantes ?

Rien de tout cela, car ici nous sommes en présence de la réalité. Or quand on mesure une grandeur (une masse en l'occurrence) on ne trouve évidemment jamais un nombre exact; la mesure est nécessairement entâchée d'une erreur (que l'on peut parfois estimer). De plus, on n'affiche qu'au maximum une décimale pour ne pas alourdir l'étiquetage (d'ailleurs qui lit ça ?); en fait, on arrondit les valeurs.

Mais qu'en est-il de la résolution d'un système de deux équations à deux inconnues lorsque l'on sait que les coefficients numériques qui y figurent sont des arrondis. Soit le système:

\[ \begin{cases} ax+by=p \\ cx+dy=q \end{cases} \]

Dans le plan \(Oxy\), il s'agit de trouver les coordonnées \((x,y)\) du point d'intersection des deux droites représentatives de chacune des équations. Pour être plus concret, prenons des données numériques: \(a=1,4 b=2,1 p=3,5\) et \(c=3,0 d=1,8 q=4,5\)

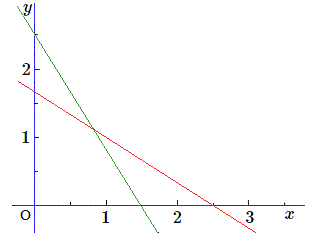
Mais ici s'agit-il de droites ?

Supposons, comme dans l'exemple que les coefficients soient tous positifs. Essayons de représenter la "droite" \(ax+by=p\). Cette droite coupe l'axe \(x\) au point d'abscisse \(p/a\) et l'axe \(y\) au point d'ordonnée \(p/b\).

Etant donné l'imprécision des valeurs \(a, b, p\) (supposées positives) on a en réalité \(a_m\lt a\lt a_M, b_m\lt b\lt b_M\) et \(p_m\lt p\lt p_M\). On voit que l'abscisse à l'origine \(x\) est comprise entre \(x_m=p_m/a_M\) et \(x_M = p_M/a_m\); de même l'ordonnée à l'origine \(y\) est comprise entre \(y_m = p_m/b_M\) et _\(M = p_M/b_m\)

On voit ainsi qu'étant donné l'imprécision affectant les mesures, il s'agit non pas d'une droite, mais d'un ensemble de droites.

Dans notre exemple numérique, \(1,35\lt a\lt 1,45\), \(2,05\lt b\lt 2,15\) et \(3,45\lt p\lt 3,55\) ce qui nous donne une abscisse à l'origine comprise entre \(2,38\) et \(2,63\) (valeurs arrondies au centième) et une ordonnée à l'origine comprise entre \(1,60\) et \(1,73\).

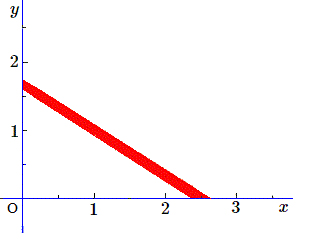
Il en est évidemment de même pour la deuxième "droite" correspondant à la deuxième équation et la résolution du système revient à trouver les points figurant dans l'intersection, et par conséquent il n'y a pas une solution, mais bien un ensemble de solutions correspondant aux coordonnées des points situés dans l'intersection.

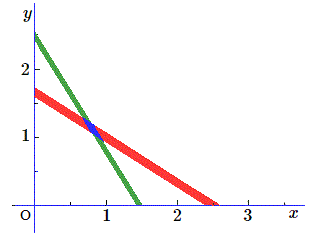
Si on veut améliorer la précision des valeurs, on ajoutera d'autres équations, ce qui limitera un peu plus le domaine des solutions.