Bientôt se disputeront les championnats nationaux de décathlon. Avez-vous déjà réfléchi à la manière dont on peut comparer les athlètes participant à cette merveilleuse épreuve. En effet ces champions doivent courir (100m, 400m, 1500m), sauter (longueur, hauteur, perche), combiner les deux (110m haies) et lancer (disque, javelot, poids). Et tout cela en deux jours ! Certains sont plus doués pour certaines épreuves. Comment comparer un athlète meilleur qu'un autre au lancer du poids, mais moins bon au saut en longueur ? Voilà le problème auquel la fédération internationale d'athlétisme "amateur" est confrontée depuis les débuts de l'existence de cette épreuve.

En fait, à chaque performance est attribué un certain nombre de points que l'on trouve dans une table régulièrement mise à jour par l'IAAF (actuellement la table "hongroise", anciennement la table "finlandaise"). La question est de savoir comment établir ces tables, comment comparer un saut de 7m60 en longueur avec un jet de 18m50 au poids. C'est ici que les statistiques pourraient intervenir.

On sait que, sous des conditions fort générales, un ensemble de données obéit à la loi normale . On peut supposer qu'il en va ainsi pour les résultats des athlètes pour un sport donné. A ce moment, il sera possible de calculer la moyenne et l'écart-type des scores obtenus. Si \(m\) désigne cette moyenne, et \(\sigma\) l'écart-type, la distribution \(F(x)\) de \(x\) obéit à la loi:

\[ F(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\frac{(x-m)^2}{\sigma}} \]

On peut normaliser en effectuant un changement d'origine de telle sorte que la moyenne vaille 0 et un changement d'unité pour que l'écart vaille 1.

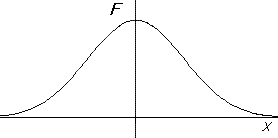\[ F(x) = \lambda e^{-\frac {x^2}{2} } \]

Chacune des épreuves sera alors représentée par la même loi \( F(x) \) et on pourra alors comparer les résultats; il ne reste plus qu'à faire choix d'une échelle.

Cette méthode, quasi impartiale, n'est hélas pas encore utilisée.