Il est de tradition de dire que nous vivons dans un espace à 3 dimensions et que seuls quelques savants ou quelques illuminés (mais est-ce bien différent?) parlent de la quatrième dimension.

Pourtant quand nous fixons rendez-vous à un ami nous ne manquons jamais de lui préciser l'heure! Nous déterminons donc tout événement par 4 paramètres: 3 coordonnées d'espace et une coordonnée de temps.

Nous utilisons donc un espace à 4 dimensions.

Comme la représentation de l'espace à 3 dimensions dans un plan pose déjà des problèmes (voir les articles sur le dessin et la perspective ), nous allons, dans une première approche, représenter les phénomènes qui se passent sur une droite et utiliser 2 dimensions, une d'espace et une de temps.

Nous pouvons ainsi représenter dans les axes ( x, t ) divers types de mouvements: par exemple un mouvement (forcément rectiligne) uniforme, une droite, un mouvement uniformément accéléré, une parabole.

Si nous considérons un objet à une dimension qui se déplace, le graphique donnera une sorte de ruban qui nous décrira la trajectoire de cet objet.

Passons en dimension 3 et supposons que nous assistions à un meeting d'athlétisme retransmis à la télévision. L'image est plane (2 dimensions) et le temps s'écoule, soit au total 3 dimensions.

On peut imaginer qu'on filme la course, qu'on découpe les images et qu'on les superpose. On obtiendrait ainsi un volume à 3 dimensions qui représenterait l'ensemble de la course.

• Une section par un plan à \(t\) constant correspondra une photographie à l'instant \(t\).
• Que dire d'une section par un plan à \(x\) constant ?

Ce sera la représentation de ce qui se passe à l'endroit donné lorsque le temps s'écoule.

Nous rencontrons, dans la vie de tous les jours, des sections à endroit constant et variable dans le temps. Ce sont les photos-finish prises pour départager les concurrents dans le cas d'une arrivée fort serrée. Ces photos nous paraissent étranges car elles sont proches d'une photo classique, mais on y constate des déformations bizarres.

En fait, ces photos sont réalisées par un appareil visant la ligne d'arrivée au travers d'une fente très mince; la pellicule se déroule derrière l'objectif. On obtient une image à 2 dimensions, une dimension d'espace (la ligne d'arrivée représentée verticalement) et une dimension de temps représentée horizontalement.

Sur l'exemple, à l'arrivée du 400 mètres, on constate que le coureur qui termine deuxième pose le pied exactement sur la ligne d'arrivée, et ce pied y demeure un temps relativement fort long.

Dans tout ce qui précède nous avons utilisé deux expressions: " à un endroit donné ", et " à un instant donné ". Cela revient à dire que nous avons supposé que le fait de se passer au même endroit ou au même instant avait un sens.

Ces deux notions, l'isotopie et la simultanéité ont été successivement remises en cause.

Tout d'abord l'isotopie: c'est Galilée qui s'est rendu compte, lors de déplacement en navire; que la notion d'immobilité n'avait pas de sens absolu. Deux observateurs en mouvement rectiligne uniforme peuvent faire les mêmes observations et chacun d'eux peut se croire immobile. C'est la relativité galiléenne ou newtonienne.

Ce n'est que bien plus tard qu' Einstein a mis en cause la notion de simultanéité. Ce fut à l'occasion de l'étude des phénomènes électromagnétiques. Contrairement à ce qui aurait du se passer, on n'avait jamais pu mettre en évidence une variation dans la valeur de la vitesse de la lumière lorsqu'elle était mesurée par des observateurs en mouvement. Une expérience fut cruciale: c'est celle de Michelson-Morley. On utilisa le mouvement de la terre (vitesse de l'ordre de 30 km/sec) pour effectuer deux mesures de la vitesse de la lumière, l'une dans la direction du mouvement de la terre et l'autre perpendiculairement: on ne constata aucune variation dans les mesures.

Comment expliquer cela ? Classiquement on aurait du rencontrer la situation suivante:

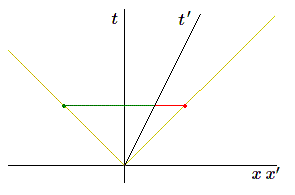Représentons en jaune les trajectoires de 2 photons partant vers la droite et vers la gauche (nous avons choisi sur les axes des unités où 1 sec = 300.000 km). Soit un observateur en mouvement rectiligne; l'axe \(t'\) représente son mouvement. Il mesure au même instant la position des 2 photons. Il est évident que la distance parcourue par le photon allant vers la droite (en rouge) sera plus petite que celle parcourue par le photon se dirigeant vers la gauche (en vert). D'après la mécanique classique, à la vitesse de la lumière on retranche ou on ajoute sa vitesse propre.

Toutefois, l'expérience confirme Qu'on n'observe aucune différence de vitesse.

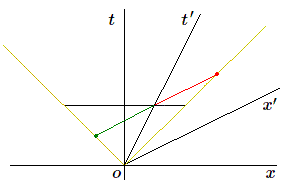La seule manière d'expliquer cette constatation expérimentale est d'admettre que la mesure de la position des 2 photons n'a pas été simultanée. Puisqu'on doit obtenir la même distance parcourue vers la droite ou vers la gauche, c'est qu'il faut considérer comme simultanés les deux événements marqués d'un point.

Pour l'observateur en mouvement ils seront simultanés alors que pour le premier observateur ils ne l'étaient pas. Les événements simultanés seront situés sur des droites parallèles à la direction de l'axe \(x'\).

Et c'est ainsi qu'Einstein montra la relativité de la notion de simultanéité !