Un des théorèmes les plus importants de la géométrie plane (peut-être faudrait-il dire le théorème le plus fondamental) est le théorème de Desargues . Il est habituellement énoncé sous la forme suivante:

Si les droites joignant les sommets homologues de deux triangles sont concourantes, les points d'intersection de leurs côtés homologues sont alignés, et réciproquement.

Cet énoncé est clairement auto-dual. La configuration correspondante est représentée ci-dessous.

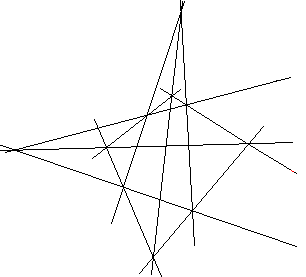
Si l'on montre ce dessin à un non-mathématicien, il y a gros à parier qu'il y verra deux triangles situés dans l'espace, projetés à partir d'un point, et il ne trouvera pas très remarquable que les plans de ces deux triangles se coupent en une droite.

Toutefois le théorème de Desargues est, en mathématiques, énoncé dans le plan. La remarque faite ci-dessus aidera à la démonstration en plongeant le plan dans l'espace et en faisant appel à un troisième triangle auxiliaire. Cependant si l'on s'interdit de sortir du plan, la démonstration devient plus ardue, voire impossible, et il convient de faire un soigneux bilan des axiomes qui ont été admis jusqu'alors. Ce bilan fait, il devient, selon les cas, possible ou impossible de démontrer ce "théorème".

Une analyse un peu plus approfondie montre que la "bonne" solution, la solution de bon sens, consiste à prendre le "théorème" de Desargues comme axiome quitte à supprimer certaines propriétés déjà admises précédemment et qui en découlent tout naturellement, telle l'existence de translations, d'homothéties, etc.

Venons-en à la démonstration du théorème (il s'agit cette fois d'un théorème) de Desargues pour un plan plongé dans l'espace (les propriétés admises sont uniquement les propriétés linéaires). Il y a bien entendu celle suggérée plus haut, mais il y a plus joli !

La configuration peut également suggérer non pas deux triangles projetés à partir d'un même point, mais aussi deux projections d'un même triangle à partir de deux points différents. Représentons cette situation:

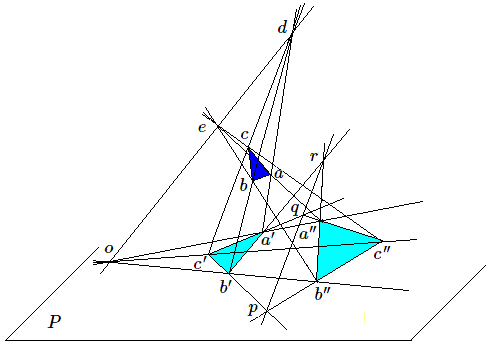
Soit le triangle \(abc\) projeté dans le plan \(P\) en \(a'b'c'\) à partir du point \(d\), et en \(a''b''c''\) à partir du point \(e\). Les droites joignant les sommets homologues \(a'a'', b'b'', c'c''\) concourent en le point \(o\) de percée de la droite de dans \(P\) ; les côtés homologues se coupent en les trois points \(p, q, r\) situés sur la droite d'intersection du plan du triangle abc avec le plan de projection \(P\).

Toutefois cette démonstration nous apprend plus. Nous nous trouvons en fait en présence de 5 points dans l'espace tels que 4 quelconques ne sont pas situés dans un même plan. Ces 5 points, pris 2 à 2 déterminent 10 droites; pris 3 à 3 ils déterminent 10 plans. Bien entendu à toute droite correspond un plan et vice-versa. Dans chaque plan il y a trois droites et chaque droite est contenue dans trois plans.

Si on sectionne cette figure spatiale par un plan non particulier, on obtient 10 points et 10 droites tels que par chaque point passent trois droites et que chaque droite contienne trois points: c'est la configuration de Desargues.

Toutefois nous avons appris que chacun des dix points joue le même rôle et qu'à chaque point est associé une droite. Cela modifie donc notre vision du théorème de Desargues et nous incite plus à parler d'une configuration de points et de droites plutôt que de deux triangles homologues.

De plus comme les 5 points de l'espace jouent un rôle équivalent, on en déduit que le groupe de la configuration de Desargues (ou plus précisément de sa structure d'incidence) est précisément le groupe Sym(5).