Une remarque préliminaire s'impose. Parler d'opérations sur des ensembles n'aucun sens. Il faut d'abord définir un ensemble \(E\) et alors seulement, on pourra définir des opérations sur les sous-ensembles de \(E\).
Dans les exemples, nous supposerons que \(E\) est l'ensemble des quadrilatères du plan. \(E\) possède divers sous-ensembles remarquables : les quadrilatères ayant un centre de symétrie (parallélogrammes), ceux ayant un axe de symétrie (les trapèzes isocèles et les deltoïdes), les rectangles, les losanges, les carrés...
Le complémentaire
Le complémentaire d'un sous-ensemble \(P\) est noté \(\overline{P}\).

Si \(P\) est l'ensemble des parallélogrammes, \(\overline{P}\) est l'ensemble des quadrilatères qui sont des non -parallélogrammes.
L'intersection
Si \(P\) et \(Q\) sont deux sous-ensembles, leur intersection est notée \(P\cap Q\). Remarquons que \(P\cap P\) = \(P\).
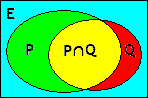
Si \(P\) est l'ensemble des losanges et \(Q\) l'ensemble des rectangles, \(P\cap Q\) sera l'ensemble des quadrilatères qui sont à la fois des losanges et des rectangles, c'est-à-dire l'ensemble des carrés.
La réunion
Nous pouvons également considérer la réunion des sous-ensembles \(P\) et \(Q\), notée \(P\cup Q\).
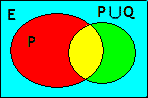
Si \(P\) est l'ensemble des rectangles et \(Q\) l'ensemble des losanges, \(P\cup Q\) sera l'ensemble des quadrilatères qui sont des rectangles ou des losanges.
L'inclusion
Si \(P\subset Q\), on peut exprimer l'inclusion de manière différente, mais équivalente : \(P\cap\bar{Q}\) est vide, ou encore \(\overline{(P\cap \overline{Q})}=E\).
En particulier l'inclusion est transitive ; on a :
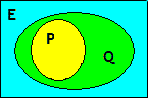
Si \(P\) est l'ensemble des rectangles et \(Q\) l'ensemble des parallélogrammes, \(P\)\subset Q\) et on a l'implication : si \(r\) est un rectangle, alors \(r\) est un parallélogramme.
Parmi toutes ces opérations il est naturel de se poser la question de savoir si certaines d'entre elles ne peuvent pas s'exprimer à l'aide d'autres. Par exemple il est évident qu'avec la réunion et le complémentaire on est à même de définir l'intersection. En effet, \(P\cap Q=\overline{(\overline{P}\cup \overline{Q})}\).
Mais il y a mieux : l'opération correspondant à la "barre de Scheffer". Aux ensembles \(P\) et \(Q\) on associe l'ensemble \(P|Q\) qui est constitué de l'ensemble des éléments qui n'appartiennent pas simultanément à \(P\) et à \(Q\) :
\[ P|Q=\overline{P\cap Q} \]Dans l'exemple où \(P\) est l'ensemble des rectangles et \(Q\) l'ensemble des losanges, \(P\)|\(Q\) est l'ensemble des quadrilatères non carrés .
Une simple observation : \(P|P = \overline{P}\) montre que la barre de Scheffer permet de définir le complémentaire dans \(E\) d'un sous-ensemble \(P\). On voit ainsi comment définir toutes les opérations sur les sous-ensembles.
A la vue des exemples ci-dessus, on voit le lien étroit qui existe entre logique , probabilités et ensembles.