Un point important du calcul algébrique est la connaissance des produits remarquables. Une vision géométrique de ceux-ci aide la mémoire.

Voyons par exemple le carré d'une somme .

Il est clair que le carré de la somme est la somme des carrés augmentée de deux rectangles, c'est-à-dire du double produit.

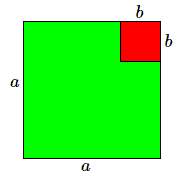
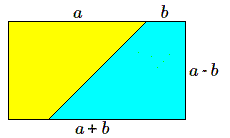
La différence de deux carrés possède également une interprétation géométrique. Soit la différence de deux carrés de côtés \(a\) et \(b\). Une petite manipulation nous fera découvrir le résultat, à savoir la factorisation en la somme \(a+b\) par la différence \(a-b\).

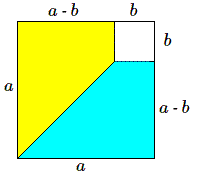
La formule donnant le cube d'une somme se retient aisément en considérant la figure ci-dessous.

On voit le grand cube de côté \(a+b\) comme somme d'un cube de volume \(a^3\), de 3 parallélépipèdes de volume \(a^2b\), de 3 autres de volume \(ab^2\) et d'un cube de volume \(b^3\).

Ces produits remarquables sont d'une grande utilité dans le calcul algébrique, mais également dans le calcul mental ! Même si les calculettes sont là pour nous aider, il n'est pas inutile de savoir calculer mentalement (les piles pourraient être usées !)

Nous avons tous appris la table de multiplication (dont nous donnons quelques exemples ). Mais savez-vous que sans trop de peine il est possible de jongler avec les nombres comme un prestidigitateur (en anglais digit = chiffre). Voici quelques trucs que l'algèbre et les produits remarquables nous aideront à justifier.

Nous n'avons que 10 doigts. Un peu trop rapidement cela nous conduirait à dire que nous ne pouvons utiliser nos doigts que pour des mini-calculs ne dépassant pas la dizaine. Affirmation bien trop rapide ! En effet sans les pouces, nous disposons à chaque main de 4 doigts formés de 3 phalanges. Cela nous permet déjà de compter jusqu'à 12 (et c'est probablement là l'origine des numérations en base 12). On peut encore aller plus loin, et c'est un excellent exercice d'agilité pour les doigts. Chaque doigt peut être plié ou "déplié". Si on considère qu'un doigt plié correspond à 0 et un doigt déplié correspond à 1, nous pouvons à l'aide de nos 10 doigts représenter tous les nombres de 0 à 1023 ! Pas mal.

Dans son ouvrage sur l'"histoire des chiffres", Georges Ifrah signale une méthode permettant d'effectuer des multiplications de deux nombres compris entre 5 et 10 en ne connaissant que les tables de multiplication jusqu'à 5.

Produit de deux nombres compris entre 5 et 10

Comment procéder uniquement avec les doigts ?

Truc : Pour chacun des deux nombres on replie un nombre de doigts égal à l'excès du nombre par rapport à 5. On additionne les nombres de doigts pliés et on multiplie par 10; on y ajoute le produit des nombres de doigts dépliés de chacune des mains. Miracle, on obtient le bon résultat !

Exemple : Soit, par exemple à multiplier 7 par 6. 7 = 5 + 2 : on abaisse 2 doigts d'une des deux mains. 6 = 5 + 1 : on abaisse 1 doigt de l'autre main. Nous sommes dans la situation suivante: On additionne les nombres de doigts pliés 2 + 1 = 3; cela donne le nombre de dizaines, c'est-à-dire 30; ensuite on multiplie les nombres de doigts dépliés: 3.4 = 12. On additionne et le résultat est 30 + 12 = 42.

Preuve : Désignons par \(a\) et \(b\) les deux nombres. \(a=5+c\): on abaisse \(c\) doigt(s) d'une des deux mains (\(5-c\) restent dépliés) \(b=5+d\): on abaisse \(d\) doigt(s) de l'autre main (\(5-d\) restent dépliés) On calcule \((c+d).10+(5-c)(5-d)\) en remplaçant évidemment \(c\) par \(a-5\) et \(d\) par \(b-5\) puisqu'on cherche le résultat en fonction de \(a\) et de \(b\). On obtient: \((a-5+b-5).10+(10-a).(10-b)\) \(=(a+b).10-100+100-10.(a+b)+a.b\) \(=ab\)

Produit de deux nombres compris entre 10 et 20

Essayons de "prolonger" la table de multiplication.

Truc : On prend le premier nombre, on y ajoute le chiffre des unités du second; on écrit (mentalement!) un 0 derrière le résultat obtenu et on ajoute le produit des chiffres des unités.

Exemple : Soit le produit de 14 par 17. 14 + 7 = 21; 210 + 4.7 = 238

Preuve : Soit à effectuer le produit des nombres \(10+a\) et \(10+b\) (avec \(a\) et \(b\) compris entre 0 et 9).

\[ \begin{align} (10+a)(10+b) & =100+10.a+10.b+a.b \\ & =((10+a)+b).10+a.b \end{align} \]

Pour ceux qui préfèrent visualiser les choses, il faut calculer l'aire du rectangle de côtés \(10+a\) et \(10+b\). Un petit dessin nous éclairera: 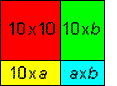Parmi les 4 rectangles qui composent le rectangle total, il y en a trois dont un des côtés vaut 10. Groupons-les: leur aire vaut \(10(10a+b)\). L'aire totale s'obtient en ajoutant celle du dernier rectangle qui vaut \(ab\). Remarquons que nous n'avons pas fait l'hypothèse que \(a\) et \(b\) sont inférieurs à 10. Cela ouvre la porte à d'autres possibilités de calcul rapide.

Produit de deux nombres de la même dizaine dont la somme des unités vaut 10

Truc : On effectue le produit de la dizaine par la dizaine augmentée de un, on multiplie par 100 et on ajoute le produit des chiffres des unités.

Exemple : Soit le produit de 33 par 37. 3.4 = 12; 1200 + 3.7 = 1221

Preuve : Soit le produit de \((10a+b)\) par \((10a+c)\) avec \(b+c=10\).

\[ \begin{align} (10a+b)(10a+c) & = 100.a.a+10.a.c+10.a.b+b.c \\ & = 100.a.a+10.a.(b + c)+b.c\\ & = 100.a.a+10.a.10+b.c\\ & = 100.a.(a+1)+b.c \end{align} \]

Carrés des nombres jusqu'à 25

Ici pas de truc ! On connaît les carrés des nombres de 1 à 10, ceux de 11 à 19 (par ce qui précède) et on fait un tout petit effort pour retenir les carrés restants; cela permettra de passer à la suite et d'être capable de calculer mentalement les carrés des nombres jusqu'à 125 !

Carrés des nombres compris entre 25 et 50

Truc : On prend la différence avec 25; on la multiplie par 100 et on y ajoute le carré de la différence avec 50.

Exemple : 43² = (43-25).100 + (50-43)² = 1800 + 49 = 1849

Preuve : Ecrivons le nombre sous la forme \(50-a\) où \(a\) est compris entre \(0\) et \(25\).

\[ \begin{align} (50-a)^2 & =2500-100a+a^2 \\ & = (25-a).100+a^2\\ & = ((50-a)-25).100+a^2 \end{align} \]

Carrés des nombres compris entre 50 et 75

Truc : idem

Exemple : 69² = (69-25).100 + (69-50)² = 4400 + 361 = 4761

Preuve : Il suffit d'écrire le nombre sous la forme 50 + a avec a compris entre 0 et 25, et de refaire le même calcul.

Carrés des nombres compris entre 75 et 125

Truc : On double le nombre, on lui retranche 100; on multiplie par 100 et on ajoute le carré de la différence avec 100.

Exemple : 118² = (2.118 - 100).100+ (118-100)² = 13600 + 324 = 13924

Preuve : Soit le nombre \(100+a\) avec \(a\) compris entre \(-25\) et \(25\).

\[ \begin{align} (100+a)^2 & =10000+200.a+a^2 \\ & = (100+2.a).100+a^2 \\ & = (200+2.a-100).100+a^2 \\ & = (2.(100+a)-100).100+a^2 \end{align} \]

Bon amusement !