Considérons le graphique de la fonction \(\mathbf{sin~}x\) (dessiné dans le plan \(\Bbb R^2\), bien qu'il existe d' autres représentations de cette fonction).
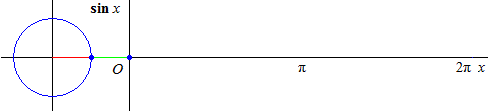
La courbe représentative présente une grande régularité et on peut sans peine recenser les isométries qui la conservent.
- Tout d'abord des translations \(T\): la fonction est périodique de période \(2\pi\). Son graphique est donc invariant pour toutes les translations d'un multiple entier de \(2\pi\).
- Il y a plus: on remarque des symétries \(S\) d'axes perpendiculaires à \(Ox\): ces axes sont distants d'un multiple entier de \(\pi\).
- De même on remarque des symétries centrales \(C\) dont les centres sont situés sur l'axe \(Ox\) et également distants de \(\pi\).
- Enfin on remarque des symétries glissées \(G\) d'axe \(Ox\) : la composante de glissement vaut \(\pi\) augmenté d'un multiple entier de \(2\pi\).
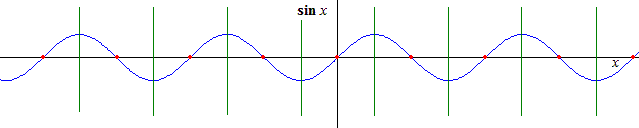
Il est tentant de composer entre elles ces diverses isométries. On obtient le tableau suivant:
| o | \(T\) | \(S\) | \(C\) | \(G\) | ||||||||||||||||
| \(T\) |
|
|||||||||||||||||||
| \(S\) | ||||||||||||||||||||
| \(C\) | ||||||||||||||||||||
| \(G\) | ||||||||||||||||||||
On constate que le regroupement des isométries en 4 classes est raisonnable et que ces classes ont entre elles un comportement cohérent.
De plus, la table de composition obtenue ressemble à celle des isométries conservant un rectangle. Ce n'est pas un hasard !
Dans le graphique de la sinusoïde, soit un point d'abscisse \(\alpha\).
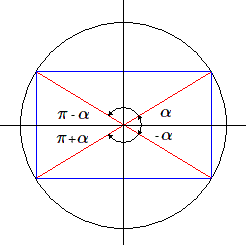
- Sous l'action des translations \(T\), nous obtenons l'ensemble des points d'abscisse \(\alpha+2k\pi\), ce qui correspond sur le cercle goniométrique, à des angles représentés par le même point.
- Sous l'action des symétries \(S\), nous obtenons les points d'abscisse \(\pi-\alpha+2k\pi\).
- Les symétries centrales donnent les points d'abscisse \(-\alpha+2k\pi\).
- Enfin les symétries glissées donnent l'ensemble des points \(\pi+\alpha+2k\pi\)
On voit ainsi que les translations \(T\) correspondent à la transformation identique, les symétries \(S\) à la symétrie par rapport à l'axe vertical (passage à l'angle supplémentaire), les symétries centrales \(C\) à la symétrie par rapport à l'axe horizontal (angle opposé) et enfin les symétries glissées \(G\) à la symétrie par rapport au centre du cercle (passage à l'angle antisupplémentaire).
La table de composition de ces 4 transformations est la même que celle des isométries d'une sinusoïde.
Les mathématiciens disent qu'il y a un (homo)morphisme du groupe des isométries conservant une sinusoïde sur le groupe des isométries d'un rectangle; on en a fait le quotient par le sous-groupe invariant \(T\) des translations.