Avez-vous déjà passé des tests ?
Une série des questions, favorites des "bons" en maths, consiste à compléter des suites de nombres, pour la plupart du temps des suites de naturels : 1, 2, 4, ... 1, 4, 9, 16, ... Facile me direz-vous. Mais est-ce vraiment le cas ?
Prenons la première. La réponse semble évidente : 8. Mais pourquoi critiquer celui qui répond 7 ? Peut-être a-t-il remarqué qu'en ajoutant 1 au premier terme on obtient 2, le deuxième terme ; ensuite, en ajoutant 2, on obtient 4, le troisième terme ; donc il ajoute 3 pour obtenir 7, le quatrième terme ! La réponse 5 peut aussi se justifier simplement : il s'agit de la liste des naturels non divisibles par 3. Mais alors ? On peut répondre n'importe quoi ! Eh bien oui ! Et même, en se justifiant d'une manière fort simple.
Si l'on songe aux approximations d'une fonction, on peut imaginer que les nombres donnés constituent les valeurs de la fonction pour quelques valeurs de la variable. Comment trouver ces fonctions, ou tout au moins quelques-unes d'entre elles : les fonctions polynômes.
Pour ne pas développer de trop longs calculs, prenons tout simplement le début de la suite 1, 2, 4, ... et cherchons les fonctions polynômes \(f(n)\) telles que \(f(1)=1, f(2)=2 \text{ et } f(3)=4 \). Evidemment un polynôme du premier degré ne peut pas convenir, il faut passer au moins au deuxième degré. Cherchons les fonctions f(n) = an² + bn + c répondant à nos conditions. On obtient le système d'équations :
\[ \left\{\begin{array}{l l} f(1) = a + b +c = 1\\ f(2) = 4a + 2b +c = 2\\ f(3) = 9a + 3b +c = 4\\ \end{array}\right.\]La solution est \(a = 1/2, b = -1/2, c = 1\) et le polynôme \((n^2- n + 2)/2\) répond à la question. Pour n=4 il vaut 7.
Remarquons au passage qu'il constitue la réponse au problème du nombre maximum de régions déterminées dans le plan (ou à l'intérieur d'un cercle) par \(n-1\) droites.
Arrêtons-nous un instant pour constater que si l'on connaît k valeurs, il est toujours possible de trouver un polynôme de degré \(k-1\) qui prend ces valeurs pour k nombres de la suite, même non consécutifs. Le système est toujours déterminé ; son déterminant est un déterminant de Vandermonde qui n'est jamais nul.
Donc, si l'on répond au problème posé par n'importe quel nombre, il existera toujours un polynôme du 3 e degré qui pourra justifier la réponse. En particulier, si l'on a répondu 8, outre la justification par les puissances de 2, on peut trouver le polynôme \(n(n^2-3n + 8)/6\) qui prend les bonnes valeurs. Moralité : ces tests ne sont pas à faire par écrit ; on n'imagine pas toujours ce qui peut se passer dans la tête de celui qui répond.
Revenons maintenant aux suites construites à partir d'un polynôme \(P(x)\) de degré m. Chacun des éléments, \(a_n\) de la suite est tout simplement la valeur de \(P(n)\). Comme nous l'avons fait à propos des suites considérons la suite des différences des éléments de cette suite. Elle est formée de polynômes \(Q(n) = P(n + 1) - P(n)\). Les termes en \(n^m\) se détruisent et les polynômes \(Q(n)\) sont de degré \(m-1\). Si nous recommençons à calculer les différences de cette nouvelle suite déterminée par les \(Q(n)\), on obtiendra des polynômes de degré inférieur et en itérant l'opération, on arrivera à de polynômes de degré 0, ce qui signifie que la différence m e sera constante. Illustrons cela par un exemple. Soit la suite donnée par le polynôme \(n(n^2 -3n + 8)/6\):
1 2 4 8 15 26 42 ...
1 2 4 7 11 16 ...
1 2 3 4 5 ...
1 1 1 1 ...
La réciproque est également valable. Si la différence \(m\) e est constante, la suite initiale est obtenue à partir d'un polynôme d'ordre \(m\). Il suffit de raisonner "dans l'autre sens". Si la constante vaut a, la différence \(m-1\) e est obtenue à partir du polynôme \(an + b\) ; la différence \((m-2)\) e est obtenue à partir du polynôme \((a/2)n^2 + (b-a^2/4)n + c\), et ainsi de suite. Voyons quelques suites intéressantes :
Suite des sommes de carrés :
0 1 5 14 30 55 91 14 ...
1 4 9 16 25 36 49 ...
3 5 7 9 11 13 ...
2 2 2 2 2 ...
On devine alors que la somme des carrés est donnée par un polynôme du 3 e degré. On procède comme tout à l'heure et à l'aide des 4 premières équations on obtient : \(P(n) = (2n^3 + 3n^2 + n)/6\). Est-ce correct ? Peut-être, mais nous avons supposé que la différence 3 e était constante mais cela n'a pas été prouvé. La formule est pourtant vraie pour \(n = 1, 2, 3, 4\) ; comment achever la démonstration ? Tout simplement par induction.
Supposons qu'elle soit valable pour la somme des carrés de \(n\) premiers naturels (ce qui est vrai jusqu'à 4).On a donc :
\(1^2 + 2^2 + 3^2 + ... + n^2 = (2n^3 + 3n^2 + n)/6 = 1/6 n(n + 1)(2n + 1)= P(n)\). Reste-t-elle vraie si l'on ajoute \((n + 1)²\) ? Le second membre devient :
\[ \begin{align} P(n)+(n+1)^2 & = 1/6 n(n + 1)(2n + 1) + (n + 1)^2 \\ & = 1/6(n + 1)[n(2n + 1) + 6(n + 1)] \\ & = 1/6 (n + 1)[2n^2 + n + 6n + 6] \\ & = 1/6 (n + 1)[2n^2 + 7n + 6] \\ & = 1/6 (n + 1)(n+2)(2n+3) \\ & = P(n+1) \end{align} \]Cette formule est donc correcte et valable pour toutes les valeurs de n. Pour la somme des cubes on peut procéder d'une manière analogue. On a :
0 1 9 36 100 225 441 ...
1 8 27 64 125 216 ...
7 19 37 61 91 ...
12 18 24 30 ...
6 6 6 ...
A présent la formule sera donnée (sous réserve d'une vérification comme ci-dessus) par un polynôme du 4 e degré. Mais avant de calculer ce polynôme, que remarquons-nous ? La somme des cubes semble toujours être égale à un carré. En effet, on obtient successivement les carrés de 0, 1, 3, 6, 10, 15, 21, ... Cette suite est intéressante ; c'est ce que les Grecs appelaient les nombres triangulaires.
Si nous avons bien deviné, la somme des n premiers cubes est égale au carré de la somme du n e nombre triangulaire :
\[1^3 + 2^3 + 3^3 + ... + n^3 = [n(n + 1)/2]^2\]La vérification est une simple démonstration par induction. Il existe toutefois une manière assez jolie de voir géométriquement cette égalité :
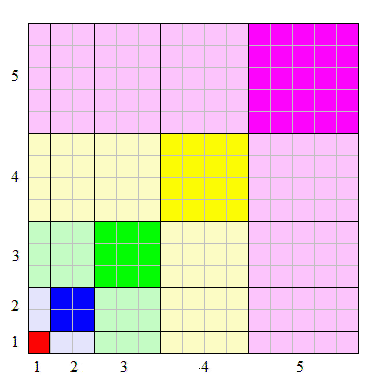
Le nombre de cases d'une même couleur (claire ou foncée) est égal au cube du nombre correspondant. Pour les nombres n impairs, on trouve, traversant la diagonale, un carré du nombre (couleur foncée) formé de \(n^2\) petits carrés et, en assemblant les rectangles (couleur claire) deux à deux (à chaque fois le plus grand avec le plus petit), on obtient \((n-1)\) carrés égaux, donc au total \(n^2 + (n-1)n^2 = n^3\) petits carrés. Pour les nombres n pairs, on trouve également le carré du nombre (couleur foncée) formé de n² petits carrés et, en assemblant les rectangles (couleur claire) deux à deux (à chaque fois le plus grand avec le plus petit), on obtient \((n-2)\) carrés égaux ; il reste deux rectangles \(n/2 x n\) qui, assemblés, fournissent le carré manquant. Au total \(n^2 + (n-2)n^2 + n^2 = n^3\) petits carrés.
Et, me direz-vous, à quoi tout cela sert-il ? A rien évidemment. Mais si vous êtes arrivés jusqu'ici, c'est que ce qui précède vous a intéressé et que ces problèmes sont jolis.
Plus sérieusement, les Grecs s'en sont occupés dans l'antiquité. De plus, vous aurez probablement remarqué l'analogie entre les suites et les différences successives, d'une part et les fonctions polynômes et les dérivées successives d'autre part. Tout cela, bien que directement inutile, a conduit à bien des développements mathématiques.