Rappelons tout d'abord la célèbre formule d'Euler :

\[ e^{ix} = \mathbf{cos}~x + i.\mathbf{sin}~x \]

ainsi que la formule de de Moivre :

\[(\mathbf{cos}~x + i.\mathbf{sin}~x)^n = \mathbf{cos}~nx+ i.\mathbf{sin}~nx\]

Ces résultats peuvent également se vérifier en utilisant les développements en série .

En partant de la formule d'Euler et en égalisant respectivement les parties réelles et les parties imaginaires et on obtient :

\[ \begin{cases} \mathbf{cos}~x = \Large{\frac{e^{i.x} + e^{-i.x}}{2}} \\ \mathbf{sin}~x = \Large{\frac{e^{i.x} - e^{-i.x}}{2i}} \end{cases} \]

Une remarque importante ! Si on n'avait jamais entendu parler des fonctions sinus et cosinus, ces formules pourraient constituer une excellente définition. En effet, la fonction exponentielle se définit de manière fort simple ; on peut se reporter à l'article sur le logarithme naturel . Cependant, les fonctions goniométriques étaient connues depuis l'Antiquité bien avant la fonction exponentielle. De plus, elles sont utilisées très tôt en physique à l'occasion de l'optique.

Les formules mentionnées plus haut permettent de vérifier immédiatement l'égalité \(\mathbf{cos}^2~x + \mathbf{sin}^2~x = 1\) et de retrouver toutes les formules usuelles de goniométrie.

Pourtant, les définitions données plus haut sont assez curieuses. En effet, les fonctions sinus et cosinus sont des fonctions d'une variable réelle. Que vient alors faire ce "\(i\)" ? Essayons de le dissimuler en posant \(t=i.x\). Rien à faire, "\(i\)" réapparaît alors dans le membre de gauche !

\[ \begin{cases} \mathbf{cos}~(t/i)= \Large{\frac{e^{t} + e^{-t}}{2}} \\ i.\mathbf{sin}~(t/i) = \Large{\frac{e^{t} - e^{-t}}{2}} \end{cases} \]

Mais, connaissant les fonctions goniométriques, on ne voit pas ce que pourraient signifier les sinus et cosinus d'une variable imaginaire ? Mystère !

Essayons une autre approche. Nous avions une fonction \(e^{ix}\) à valeurs complexes et nous avons construit, à partir d'elle, deux fonctions à valeurs réelles correspondant l'une à la partie réelle, l'autre à la partie imaginaire.

Après notre tentative pour faire disparaître le "\(i\)", nous avons obtenu deux fonctions à partir de la fonction exponentielle \(e^x\) : la fonction \((e^x+e^{-x})/2\) et la fonction \((e^x-e^{-x})/2\). Ces deux fonctions sont intéressantes ; l'une est une fonction paire \((f(-x) = f(x))\), l'autre une fonction impaire \((f(-x)=-f(x))\). Plus généralement, étant donné une fonction réelle \(f(x)\), on peut toujours la décomposer de manière unique en somme de deux autres:

\[ f^+(x) = \frac{f(x) + f(-x)}{2}~~~~ \text{et} ~~~~f^- (x)=\frac{f(x) - f(-x)}{2} \]

La première est une fonction paire, la seconde est une fonction impaire.

Cette décomposition nous rappelle, d'une certaine manière, celle obtenue en séparant composante réelle et composante imaginaire d'une fonction à valeurs complexes pour aboutir à deux fonctions réelles intéressantes. Qu'en est-il ici ? Introduisons donc, à partir de la fonction exponentielle \(e^x\), deux fonctions réelles que nous désignerons, par analogie avec ce que nous avions plus haut, par \(\mathbf{cosh}\) et \(\mathbf{sinh}\). (Nous justifierons dans un instant ce choix qui pourrait paraître curieux).

\[ \begin{cases} \mathbf{cosh}~(x)= \Large{\frac{e^{x} + e^{-x}}{2}} \\ \mathbf{sinh}~(x) = \Large{\frac{e^{x} - e^{-x}}{2}} \end{cases} \]

En utilisant le développement en série de MacLaurin de \(e^x\), on obtient :

\[ \mathbf{cosh~}x = 1 + \frac {x^2} {2!} + \frac {x^4} {4!} + \frac {x^6} {6!} + \frac {x^8} {8!} + ...\] \[ \mathbf{sinh~}x = x + \frac {x^3} {3!} + \frac {x^5} {5!} + \frac {x^7} {7!} + \frac {x^9} {9!} + ...\]

Tout comme avec les fonctions \(\mathbf{sin}\) et \(\mathbf{cos}\) nous avions obtenu \(\mathbf{cos}^2~x + \mathbf{sin}^2~x = 1\), les carrés de ces nouvelles fonctions satisfont à une relation analogue : \(\mathbf{cosh}^2~x - \mathbf{sinh}^2~x = 1\).

Avec les fonctions trigonométriques, on remarquait que \(x=\mathbf{cos}~t\) et \(y=\mathbf{sin}~t\) sont les équations paramétriques du cercle \(x^2+y^2=1\). Ces fonctions sont parfois qualifiées de fonctions circulaires. A présent, on constate que \(x=\mathbf{cosh}~t\) et \(y=\mathbf{sinh}~t\) représentent les équations paramétriques de l'hyperbole \(x^2-y^2=1\), plus précisément de la moitié positive de l'hyperbole :

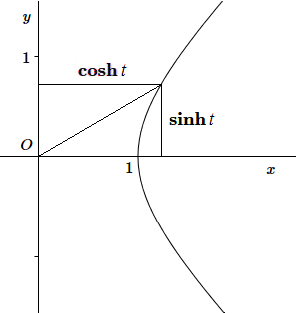
Voilà donc la justification du "h" ajouté au nom des fonctions goniométriques traditionnelles. Ces fonctions sont dénommées "cosinus hyperbolique" et "sinus hyperbolique" et possèdent une grande analogie avec les fonctions circulaires.

On peut, sans difficulté, calculer les analogues des autres identités classiques de la goniométrie. On remplace \(\mathbf{cos}\) par \(\mathbf{cosh}\) et \(\mathbf{sin}\) par \(i.\mathbf{sinh}\). En égalant soit les parties réelles soit les parties imaginaires, on obtient les formules de la trigonométrie hyperbolique.

On peut également définir d'autres fonctions hyperboliques, notamment la tangente hyperbolique qui est tout simplement le rapport de sinus hyperbolique à cosinus hyperbolique. On vérifie que la dérivée de \(\mathbf{sinh~}x\) est \(\mathbf{cosh~}x\) et celle de \(\mathbf{cosh~}x\) est tout simplement \(\mathbf{sinh~}x\) (le signe - a disparu). Signalons également les formules exprimant les sinus et cosinus hyperboliques de \(x\) en fonction de la tangente hyperbolique de \(x/2\) que nous noterons \(t\) :

\[\begin{cases} \mathbf{sinh~}x = \Large\frac{2t}{1-t^2} \\ \mathbf{cosh~}x = \Large\frac{1+t^2}{1-t^2} \\ dx = \Large\frac{2dt}{1+t^2} \end{cases}\]

Ces formules sont parfois utiles lors du calcul d'intégrales.

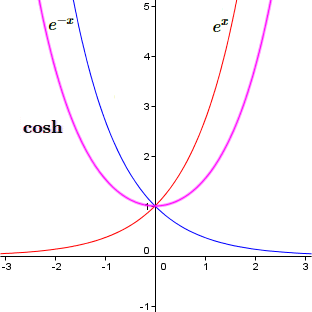
Voici les graphiques de ces nouvelles fonctions :

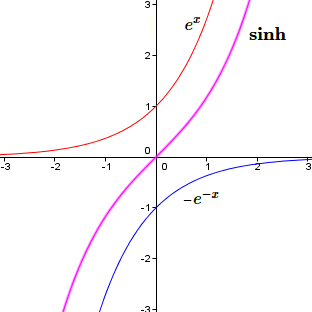
Dans les axes, nous avons représenté en rouge la fonction \(e^x\), en bleu la fonction \(e^{-x}\) ou \(-e^{-x}.\)

Enfin, il reste à trouver une interprétation de la variable qui intervient comme argument des fonctions \(\mathbf{cosh}\) et \(\mathbf{sinh}\). Dans le cas de la trigonométrie \(\mathbf{cos~}t\) et \(\mathbf{sin~}t\), la variable \(t\) pouvait être interprétée dans le cercle trigonométrique (de rayon unité) de plusieurs manières équivalentes:

1. \(t\) est la mesure de l'arc intercepté
2. \(t\) est la valeur, exprimée en radians, de l'angle au centre
3. \(t\) est le double de la mesure de l'aire du secteur circulaire

Seule, la troisième propriété peut se généraliser aisément dans le cas où le cercle \(x^2+y^2=1\) est remplacé par l'hyperbole \(x^2-y^2=1\). Historiquement, c'est le calcul (assez compliqué) de cette aire qui a conduit Vincenzo Riccati à la définition des fonctions hyperboliques

Calculons en fonction de \(t\) l'aire d'un secteur de l'hyperbole définie par :

\[ \begin{cases} x = \mathbf{cosh~}t \\ y= \mathbf{sinh~}t \end{cases} \]

Pour cela, effectuons une rotation d'un quart de tour qui nous conduit à une hyperbole dont les asymptotes sont les axes coordonnés.

\[ \begin{cases} x' = \frac{\sqrt{2}}{2}(x + y)=\frac{\sqrt{2}}{2} (\mathbf{cosh~}t + \mathbf{sinh~}t)=\frac{\sqrt{2}}{2}e^{t}\\ y' = \frac{\sqrt{2}}{2}(x - y)=\frac{\sqrt{2}}{2}(\mathbf{cosh~}-\mathbf{sinh~}t)= \frac{\sqrt{2}}{2} e^{-t} \end{cases} \]

Effectuons une homothétie de rapport \(\sqrt{2}\) (les aires seront ainsi doublées) afin de simplifier le schéma. Le calcul de l'aire d'un secteur hyperbolique en fonction de t peut alors être visualisé de manière simple. Que vaut l'aire \(A\) du secteur hyperbolique dessiné en vert ?

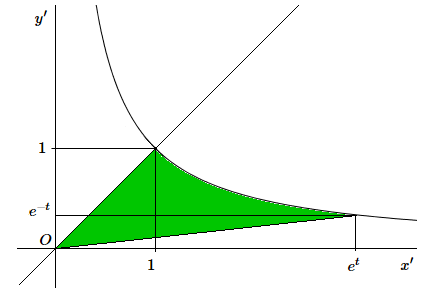
On a:

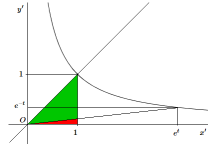
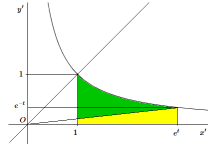
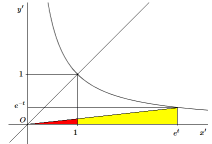
ou de manière plus traditionnelle: \[ A =\int_ {0} ^{1} x~dx~~~~~~~+~~~~~~~\int_ {1} ^{e^t} \frac{1}{x}~dx~~~~~~~-~~~~~~~\int_{0}^{e^t} e^{-2t}x~dx \]

mais le premier et le dernier terme de la somme sont égaux et se détruisent ; on obtient donc (voir Logarithme naturel ): \[ A=\int_ {1} ^{e^t} \frac{1}{x}~dx = \mathbf{ln~}e^t = t \]

Comme les aires ont été doublées, l'aire du secteur hyperbolique vaut : \(A= \frac{t}{2}\) un résultat analogue à celui de l'aire du secteur circulaire d'angle \(\varphi\) qui vaut \(a = \frac{\varphi}{2}\).