Il existe une très belle transformation qui n'est malheureusement plus guère étudiée: l' inversion .

Donnons-en la définition dans le plan (la généralisation à l'espace est évidente). Soit un point \(o\) du plan. Le transformé \(p'\) d'un point \(p\) est aligné avec \(o\) et \(p\), et tel que le produit \(op.op'\) est une constante appelée puissance. (Remarquons que le point \(p\) est évidemment le transformé de \(p'\)). On peut toujours "corriger" l'inversion par une homothétie de centre \(o\), de telle sorte que la puissance devienne positive. Dans ce cas il existe des points fixes situés sur un cercle dont le rayon vaut la racine carrée de la puissance de l'inversion.

Cette transformation est bien définie sauf en ce qui concerne le point \(o\) qui est appelé pôle de l'inversion. Lorsqu'un point se rapproche du pôle son transformé s'éloigne de plus en plus. On peut imaginer que l'on complète le plan par un point "à l'infini" qui sera considéré comme l'image du pôle \(o\). Dès lors l'inversion devient une bijection dans ce plan complété par un point. Il s'agit alors du plan conforme.

Comment se présentent les équations d'une inversion de pôle \(o\) et de puissance \(k\) ? Si on choisit un repère orthonormé centré en \(o\), et si \((x,y)\) sont les coordonnées d'un point \(p\), les coordonnées de \(p'\) sont proportionnelles à celles de p, soit \((x',y')=(tx, ty)\). Exprimons que le produit \(op.op'\) vaut \(k\), ou encore que le produit des carrés des distances vaut \(k^2\). On a \((x^2+y^2)(t^2x^2+t^2y^2)=k^2\), d'où \(t=k/(x^2+y^2)\).

Les équations de l'inversion sont donc:

\[ \begin{cases} x'=kx/(x^2+y^2) \\ y'=ky/(x^2+y^2) \end{cases} \]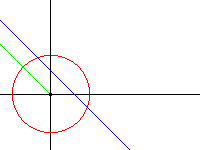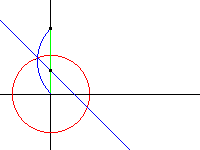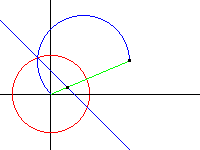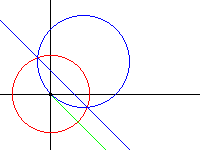

Cette transformation très simple a pourtant, aux yeux de certains, un gros défaut: elle n'est pas linéaire. Une droite d'équation \(ax+by+c=0\) a pour transformée la courbe d'équation \(akx/(x^2+y^2)+bky/(x^2+y^2)+c=0\). On voit que c'est celle d'un cercle \(kax+kby+c(x^2+y^2)=0\) passant par l'origine.

Dès lors on peut se poser la question du transformé d'un cercle quelconque:

\[ a(x^2+y^2)+bx+cy+d=0 \]

Nous avons vu plus haut comment se transformaient \(x'\) et \(y'\). Calculons à présent la valeur de l'expression \((x'^2+y'^2)\) qui apparaît dans l'équation des cercles ; on obtient :

\[(kx/(x^2+y^2))^2 + (ky/(x^2+y^2))^2 = k^2(x^2+y^2)/(x^2+y^2)^2 = k^2/(x^2+y^2)\]

La transformée du cercle \(a(x'^2+y'^2)+bx'+cy'+d=0\) est donc :

\[ ak^2/(x^2+y^2)+bkx/(x^2+y^2)+cky/(x^2+y^2)+d = 0 \]

c'est-à-dire, en multipliant par \((x^2+y^2)\) et en simplifiant :

\[ k^2a+kbx+kcy+d(x^2+y^2)=0 \]

On voit ainsi que l'ensemble des droites et des cercles, l'ensemble des cycles, est conservé. En fait l'inversion est une transformation linéaire opérant sur les cycles .

Les équations de l'inversion ressemblent fort à celles donnant les parties réelles et imaginaires de l'inverse \(x'+iy'\) d'un nombre complexe \(x+iy\). Seule l'ordonnée \(y'\) a changé de signe. L'inversion n'est autre que la transformation qui applique \(z\) sur \(1/\bar{z}\). En utilisant le plan de Gauss, on sait que l' ensemble des cycles ( droites et cercles ) s'écrit:

\[ az\bar{z}+k\bar{z}+\bar{k}z+d=0 \]

avec \(a\) et \(d\) réels et il est évident que cet ensemble est conservé par inversion.

On peut visualiser l'inversion d'une manière fort simple.

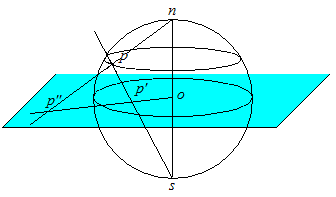Soit une sphère \(S\) de centre \(o\) et deux points antipodes \(n\) et \(s\) (parlons du pôle Nord et du pôle Sud). Si \(p\) est un autre point de \(S\) en projetant à partir des pôles sur le plan de l'équateur on obtient deux projections \(p'\) et \(p''\). On voit immédiatement que ces deux points se correspondent dans une inversion de pôle \(o\) et de puissance égale au carré du rayon de \(S\). Il suffit pour celà de comparer les deux triangles semblables \(op''n\) et \(osp'\); on obtient \(op'/os = no/p''o\), c'est-à-dire \(op'.op''= R^2\)

On compose ainsi deux projections stéréographiques , et par conséquent l'inversion conserve les angles. C'est une transformation conforme .